Простейшие уравнения и неравенства, содержащие модуль.
I. Уравнение вида |f(x)| = a (1)
Понятно, что при a < 0 уравнение (1) не имеет решений.
При a = 0 уравнение имеет вид : |f(x)| = 0
Это возможно, если f(x) = 0
ПРИМЕР: | 3x – 1| = 0 < = > 3x – 1 = 0 < = > x = 1/3.
При a > 0 Уравнение (1) разбивается на два уравнения: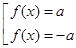 
Данную совокупность можно решать , найдя корни каждого уравнения по отдельности.
ПРИМЕР: | 4x + 5| = 6
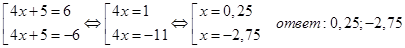
II. Неравенство вида |f(x)| < a (2)
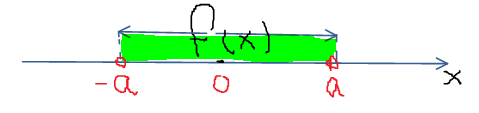рис 1.
Замечаем, что при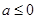 
неравенство (2) не имеет решений
Геометрический смысл понятия модуля из числа m, т.е. |m| означает расстояние от 0 до точки с координатой m
В нашем случае это расстояние от 0 до точки с координатой f(x). Неравенство (2) можно прочитать так: На числовой прямой, найти все точкиf(x), удаленные от 0 на расстояние, меньшее числа а
Тогда рисунок (1) понятен: f(x) располагается в зеленой зоне и неравенство (2) решается так:
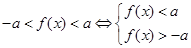
Пример: Решите неравенство: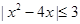 
Решение:
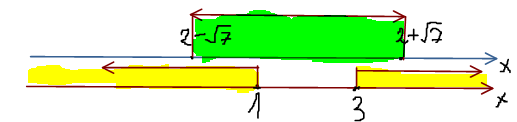
Находим пересечение множеств решений каждого неравенства (совпадение зеленого и желтого цвета: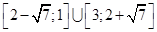 
III. Неравенство вида |f(x)| > a (3)
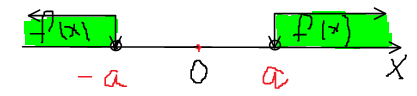рис 2
В этом случае , неравенство (3) можно прочитать так: На числовой прямой, найти все точкиf(x), удаленные от 0 на расстояние, большее числа а.
ПРИМЕР: |16 – x2| >13
Решение: 
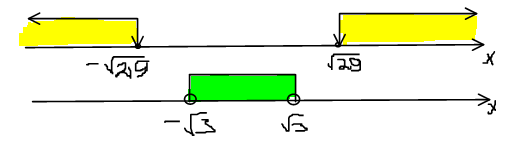
Желтым цветом показано решение неравенства 
, зеленым цветом показано решение второго неравенства 
.
Объединяя решения ( смотрим интервалы, где есть и желтый и зеленый цвета), записываем ответ: 
IV. |f(x)| = |g(x)|; |f(x)| < |g(x)|; |f(x)| > |g(x)|
Эти уравнения и неравенства решаются методом возведения обеих частей в квадрат, используя свойства числовых неравенств : 0 < a < b = > a2 < b2 и свойство модуля, что (|a|)2 = a2
ПРИМЕРЫ:
|2x + 1| = | 2x – 2 |
Решение: (|2x + 1|)2 = (| 2x – 2 |)2
(2x + 1)2 – (2x – 2)2 = 0 Воспользуемся формулой разности квадратов
(2x + 1 – 2x + 2)(2x + 1 + 2x – 2) = 0
3(4x – 1 ) = 0
x = 0,25
Решите неравенство: | 2x – 5 | < | x + 3|
Решение: (2x – 5)2 < ( x + 3)2
( 2x – 5 – x – 3)(2x – 5 + x + 3) < 0
( x – 8)(3x – 2) < 0
( 2/3; 8 )
Задания для подготовки к проверочной работе.
1.1 Решите уравнения и неравенства:
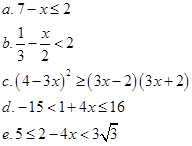
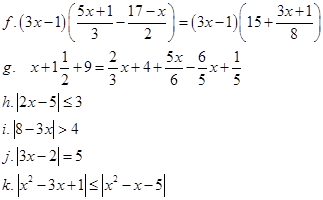
1.2 Данные между годовым доходом населения и сбережениями занесены в таблицу:
| Доход ( в год, $) | сбережения (в год $) |
| – 500 | |
а) Установить зависимость доходами и сбережениями (что есть х и что у)
б) Напишите уравнение этой зависимости, выдвинув гипотезу о наличии линейной связи.
в) Рассчитайте объем сбережений при уровне дохода 12500$
г) Рассчитайте угловой коэффициент и пересечение прямой с осью Оу.
д) Какой экономический смысл имеет коэффициент, полученного уравнения? Постройте график этой зависимости.
1.3 Изобразите на координатной плоскости множество точек, удовлетворяющих неравенствам:
a) 2x – 3y > 1 b) x + y ≤ 2 c) x – |y| > 1 d) |x| + |y| ≤ 1
1.4 При каких значениях m
a. уравнение 2x – 5 – mx не имеет решений
b. уравнение mx = 4x + 12 имеет одно решение
c. уравнение 2mx + 3 = 2m – x имеет бесконечное множество решений ?
2.5 Решите неравенство ax > 1 при всех значениях a