Задание 8.
| В номерах 1-15Пользуясь формулой Остроградского-Гаусса, вычислить интегралы: | В номерах 16-30Используя формулу Стокса, вычислить интегралы: | ||
 где σ – внешняя поверхность эллипсоида где σ – внешняя поверхность эллипсоида 
|  где где  – периметр треугольника с вершинами – периметр треугольника с вершинами 
| ||
 где σ – внутренняя поверхность куба, ограниченного плоскостями где σ – внутренняя поверхность куба, ограниченного плоскостями 
|  где где  – периметр треугольника с вершинами – периметр треугольника с вершинами 
| ||
 где σ – внешняя поверхность сферы где σ – внешняя поверхность сферы 
|  где где  – окружность – окружность  в качестве поверхности в качестве поверхности  принять полусферу принять полусферу 
| ||
 где σ – внешняя сторона пирамиды, ограниченной плоскостями где σ – внешняя сторона пирамиды, ограниченной плоскостями 
|  где где  – –  и и  окружность окружность 
| ||
 где σ – внешняя сторона поверхности, расположенной в первом октанте и составленной из цилиндра где σ – внешняя сторона поверхности, расположенной в первом октанте и составленной из цилиндра  и плоскостей и плоскостей 
|  где где  - периметр треугольника с вершинами - периметр треугольника с вершинами 
| ||
 если N – внешняя нормаль к поверхности сферы если N – внешняя нормаль к поверхности сферы 
|  где где  - периметр треугольника с вершинами - периметр треугольника с вершинами 
| ||
 где N – внешняя нормаль к поверхности сферы где N – внешняя нормаль к поверхности сферы 
|  , где , где  - окружность - окружность  . .
| ||
 ,где σ – верхняя поверхность плоскости ,где σ – верхняя поверхность плоскости  , расположенной в первом октанте. , расположенной в первом октанте.
|  где где  - контур, образованный пересечением поверхности - контур, образованный пересечением поверхности  с плоскостями координат. В качестве поверхности σ принять расположенную в первом октанте часть данной поверхности. с плоскостями координат. В качестве поверхности σ принять расположенную в первом октанте часть данной поверхности.
| ||
 ,где σ – внешняя сторона поверхности, ограниченной цилиндром ,где σ – внешняя сторона поверхности, ограниченной цилиндром  и плоскостями и плоскостями 
|  где где  - периметр треугольника с вершинами - периметр треугольника с вершинами 
| ||
 где σ – внешняя поверхность полусферы где σ – внешняя поверхность полусферы  и плоскости и плоскости 
|  где где  - периметр треугольника с вершинами - периметр треугольника с вершинами 
| ||
 где σ - внешняя сторона поверхности, ограниченной конусом где σ - внешняя сторона поверхности, ограниченной конусом  и плоскостью и плоскостью 
| 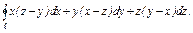 где где  - периметр треугольника с вершинами - периметр треугольника с вершинами 
| ||
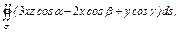 где σ – внешняя сторона поверхности, ограниченной плоскостями где σ – внешняя сторона поверхности, ограниченной плоскостями 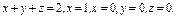
|  где где  - контур пересечения сферы - контур пересечения сферы  с плоскостью с плоскостью 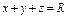 . За поверхность σ принять часть сферы, расположенную в первом октанте. . За поверхность σ принять часть сферы, расположенную в первом октанте.
| ||
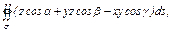 где σ – внешняя сторона поверхности цилиндра где σ – внешняя сторона поверхности цилиндра  и плоскостей и плоскостей 
|  где где  - контур пересечения параболоида - контур пересечения параболоида  с плоскостями с плоскостями 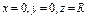 . За поверхность σ принять параболоида, расположенную в первом октанте. . За поверхность σ принять параболоида, расположенную в первом октанте.
| ||
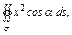 где σ – внешняя сторона поверхности, ограниченной плоскостями где σ – внешняя сторона поверхности, ограниченной плоскостями 
| 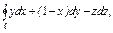 где где  - контур пересечения полусферы - контур пересечения полусферы  и цилиндра и цилиндра  . За поверхность σ принять данную полусферу. . За поверхность σ принять данную полусферу.
| ||
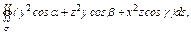 где σ – внешняя поверхность сферы где σ – внешняя поверхность сферы 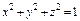
| 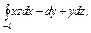 где где  - контур пересечения сферы - контур пересечения сферы  и плоскости и плоскости 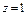 . За поверхность σ принять верхнюю часть сферы. . За поверхность σ принять верхнюю часть сферы.
|