Построение теней здания

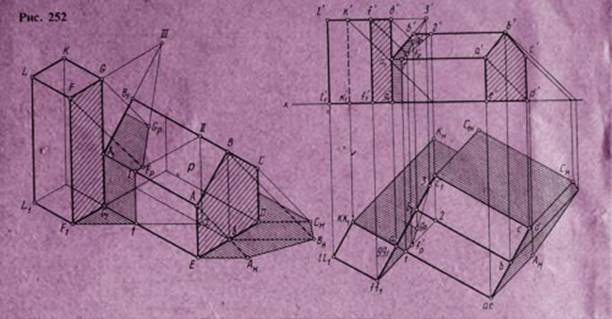
Пример построения теней промышленного здания, схематично изображенного в прямоугольной изометрии и ортогональных проекциях, приведен на рис. 252. Заданное здание по форме представляет пятиугольную призму с основанием ABCDE и прямоугольный параллелепипед с верхним основанием KLFG. Для большей наглядности на ортогональном чертеже боковые грани призм расположены не параллельно фронтальной плоскости проекций V.

На прямоугольном параллелепипеде контур собственной тени будет проходить через точки FGKK1L1F1F, поэтому в собственной тени будут правая передняя (видимая) грань параллелепипеда FGG1F1 и задняя правая (невидимая) грань KGG1K1. У пятиугольной призмы в тени находится основание ABCDE и задняя грань, примыкающая к стороне основания CD. Передний скат крыши (грань, примыкающая к стороне АВ) будет освещен, а будет ли освещен задний скат крыши (грань, примыкающая к стороне основания ВС), сказать трудно, контур собственной тени пятиугольной призмы недостаточно ясен. Поэтому построение начинаем с определения контура падающей тени от пятиугольной призмы.

Определяем тени АH, ВH, СH точек А, В и С и отмечаем падающую тень основания призмы ЕАHВHСH- Далее контур падающей тени проходит через тень СHС1H ребра призмы СС1 (CHC1H параллельна СС1 так как это ребро параллельно плоскости Н) и замыкает падающую тень пятиугольной призмы — тень C1HD1H - Таким образом, контур падающей тени ограничивает тень ребра CC1 — по этому ребру будет проходить и контур собственной тени призмы, т. е. оба ската крыши (обе верхние грани призмы) будут освещены.

Тень от прямоугольного параллелепипеда будет падать на плоскость H и на поверхность пятиугольной призмы. Строим падающую тень от контура собственной тени параллелепипеда. Тень от вертикального ребра FF1 на плоскость H совпадает с проекцией луча света на эту плоскость, по грани AEG1A1 пятиугольной призмы тень от FF1 пойдет параллельно прямой FF1 (эта прямая параллельна указанной грани).

В точке 1 тень от прямой FF1 изломится и пойдет далее по грани ABB1A1 в точку 2, расположенную на ребре ВВ1 но закончится она в точке Fp, в которой луч света, проведенный через точку F, пересекает плоскость Р на прямой 1—2 (грань ABB1A1). Далее тень будет бросать горизонтальная прямая FG. Тень на плоскость Р от этой прямой будет проходить через построенную точку Fp и точку 3, в которой прямая FG пересечет плоскость Р, если и прямую и плоскость Р мысленно продлить направо. Эта тень будет ограничена тенью Gp, падающей на плоскость Р от точки G. Тень от отрезка прямой GK, параллельного плоскости Р, будет равна и параллельна этому отрезку. В ортогональных проекциях тень от этого отрезка частично упадет на плоскость Н, на которую будет падать тень и от ребра параллелепипеда KK1 (на изометрии она не видна, а на ортогональных проекциях совпадает с горизонтальной проекцией луча света, проведенного через точку К1).

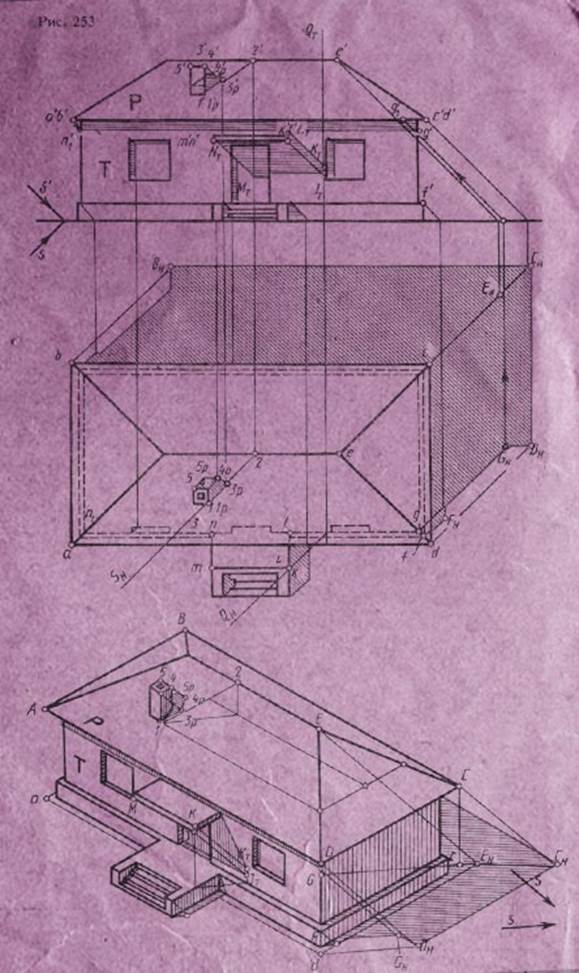
Пример построения в прямоугольной изометрии и ортогональных проекциях теней другого здания показан на рис. 253. Так как контур собственной тени на крыше и этого здания недостаточно ясен, построение начинаем с определения падающей на горизонтальную плоскость проекций тени. Для этого через характерные точки здания — углы карниза D, С, В, границу конька крыши (точку Е) — проводим лучи света параллельно заданному направлению и определяем тени указанных точек DH, СH, ВH, ЕH. Тени от углов здания, вертикальных прямых совпадут с горизонтальной проекцией лучей света, проведенных через эти прямые. Падающие тени от свесов карнизов AD, DC, СВ, ВА будут параллельны указанным прямым, так как последние параллельны горизонтальной плоскости проекций Н.

В результате получаем контур падающей тени, который проходит через точки DHCHBH и т. д. Тень от точки Е — ЕH попала внутрь контура падающей тени, поэтому вся крыша будет освещена, а контур собственной тени проходит по свесам карнизов, а также по правому переднему и левому заднему углам здания.

Рассмотрим ход построения тени, падающей от трубы на передний скат крыши, плоскость которого обозначим буквой Р.

Находим тень от вертикального ребра трубы 1—3. Тень от точки 1 будет в той же точке, так как она принадлежит плоскости Р. Для построения тени от точки 3 проводим через эту точку луч света и определяем точку пересечения его с Р. С этой целью через луч проведена вспомогательная горизонтально проецирующая плоскость S, которая пересекает скат крыши Р по прямой 1—2. В пересечении прямой 1—2 и луча, проведенного через точку 3, находится искомая тень Зр. Аналогично строятся тени от точек 4 и 5, через которые проходит контур собственной тени. Следует обратить внимание на то, что тень 4р — 5р параллельна прямой 4 — 5, так как эта прямая параллельна плоскости Р.

Для построения падающей тени от свеса кровли AD на плоскость Т направим через угол свеса А луч света, который пересечет плоскость Т в точке N1. Через точку n’1проведем прямую, параллельную AD, которая и будет падающей тенью от свеса кровли на плоскость стены Т.

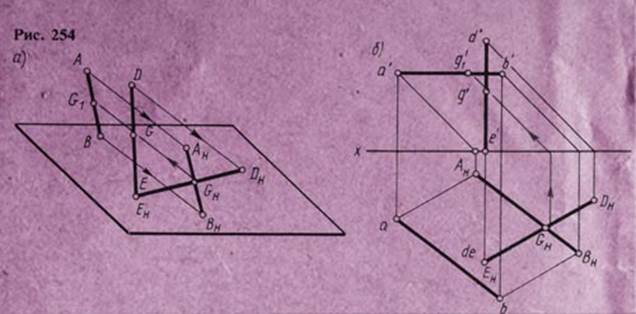
Тень от свеса кровли AD на плоскость T можно построить также способом обратного луча, сущность которого заключается в следующем (рис. 254, а и б).

Пусть ED и АВ — две скрещивающиеся прямые, a EHDH и АНВН — тени от них на плоскость Н. Если из точки пересечения теней этих прямых GH провести луч параллельно лучам света, но в обратном направлении до пересечения с прямой ED и АВ, то на прямой ED получим точку G, которая будет тенью от точки G1 лежащей на прямой АВ.

На рис. 255 приведено построение методом обратного луча тени от прямой AD (свес кровли) на плоскость Т. Тень пойдет через точку G (g’; g) на плоскости Т параллельно AD, так как свес кровли параллелен плоскости стены Т.

Построение тени от козырька над входом, крыльца, в нишах оконных и дверных проемов подробно рассмотрено в предыдущей статье (см. рис. 245… 251).