Листинг 4.1. программа, иллюстрирующая применение метода резолюции

 

predicates

likes(symbol,symbol)

food(symbol,symbol)

 

clauses

S2 likes(bill,pizza):-

food(pizza,italiano).

S3 food(pizza,italiano).

 

 

S2 и S3 –родительские предложения

В качестве S1 будет выступать цель goal: likes(bill,pizza), которая поступит на компилятор в виде отрицания.

Опровержение отрицания демонстрируется так: допущение отрицания цели ведет к противоречию.

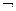likes(bill,pizza) подаем на вход системы резолютивного вывода. Система должна опровергнуть это отрицание при помощи других предложений программы.

 

 

Рис. 4.1. Применение принципа резолюции

 

 

Для верхнего случая : S1: 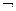A.

S2:A:-B.

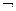S: B

 

Для нижнего случая : S1: 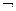A

S2:A

S: противоречие

В данном примере оказалось достаточно двух шагов вывода. Если предположить, что мы не отказываемся от предложений S2 и S3, и сами они не являются противоречивыми, то отсюда следует, что они совместно противоречат S1, то есть подтверждают отрицание S1, а следовательно, ответ –ДА.

В общем виде:

S1: 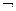(A₁,..,A_n)

S2: A_к:-B₁,..,B_m где 1<=к<=n

Некий предикат A_k из отрицания S1 совпадает с головой правила S2.В этой ситуации шаг вывода заменяет A_k в S1 на подцель из S2, и в качестве резольвенты получаем s: 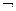(A₁,..,A_k-1,B₁,..,B_m,A_k+1,..,A_n).

 

Если на запрос можно получить ответ на основе знаний, закодированных во входных допущениях, то система обязательно его получит. Ответственность за построение вывода, за управление протоколом связываний и извлечения ответа может быть полностью возложено на систему.

Каждое вычисленное решение обладает требуемым свойством – оно логически следует из данных допущений. Очень немногие из формальных систем программирования обладают этими качествами.