Вопросы и задания для самостоятельной работы 6 страница

Прием умножения суммы на число закрепляется при выполнении следующих упражнений: «Представь число 183 в виде суммы двух (трех) слагаемых, чтобы его легко можно было умножить на 5» и т. д.; «Умножь удобным способом: (300 + 40 + б) 3, (200 + 70 + +6)5» и т. д.

Умножение разрядных чисел на однозначное число двузначные и трехзначные разрядные числа в пределах тысячи учащиеся умножать умеют. В более сложных случаях — умножение многозначного разрядного числа используется прием замены многозначного множителя однозначным именованным числом.

Вначале школьники вспоминают, как, например, ЗОО умножается на З: «ЗОО—это З сотни, а З сот..З=9 сот. Значит, 300.3= = 900». Этот прием обобщается для случаев 3 000 3, 5 000. 6, ЗОО . 8, 900 . 9, 20 000 . 7 и т. д. В случае, например, 20 000. 7, учащиеся рассуждают так: «20 000 это 2 десятка тысяч; 2 десятка тысяч умножить на 7, получим 14 десятков тысяч, т. е. 140 000». Рас- суждения выполняются учащимися устно, результат записывается.

Умножение многозначного числа на однозначное. Учащиеся могут самостоятельно определить способ умножения многозначного числа на однозначное. Задача учителя состоит в том, чтобы подобрать систему произведений, расположенных по возрастающей сложности.

Самый простой случай, когда неполные произведения являются разрядными числами:

1 232.3 =(1 000 + 200 + ЗО + 2). 3 = 1 000.3 + 200.3 +

30.3+2.3=3000+600+90+6=3696;

20341 .2 =(20 000 + 300+40 + 1). 2 = 20000.2 + 300.2 +

+40.2+1 .2=4Об82

При решении уже второго, третьего примеров такого рода учащимся предлагается выполнять промежуточные действия в уме и записывать сразу ответ.

В более сложных случаях (112053 3, 7083 . 2) целесообразно все вычисления производить с подробной записью промежуточных операций. Особенность этих примеров в том, что неполные произведения учащиеся в состоянии сложить в уме.

Наконец, рассматриваются самые сложные случаи: 2 345 3,

6189 . 2, 7 542 . 7 и и. д. Чтобы вычислить эти произведения в уме,

можно найти значения неполных произведений. Сумма этих произведений вычисляется в столбик. Пусть, например, умножается

64 579 . 4. Учащиеся записывают:

64579.4 = 240 000 + 16000 + 2000 + 280 + 36.

Затем эти числа складываются в столбик:

Возможно, достаточно рассмотреть одно-два таких произведения, чтобы учащиеся почувствовали трудоемкость такого алгоритма умножения. Так создается психологическая предпосылка к изучению алгоритма умножения в столбик.

Умно жен и е в столбик. Для обучения учащихся умножению в столбик целесообразно использовать методику, которую можно назвать «обучение по образцу». При этом учитель на конкретных примерах показывает, в чем состоит новый прием, акцентирует внимание учащихся на основных его операциях (пояснениями или графически). Учащиеся под наблюдением учителя воспроизводят этот прием. Обучение по образцу не исключает, конечно, элементов проблемного обучения.

Рассматривается умножение трехзначного числа на однозначное, которое вычислить устно трудно, например 465 7. Учитель записывает множители в столбик, подчеркивая, что однозначный множитель располагается под разрядом единиц первого множителя. На первых порах на доске (в тетрадях) колонки клеток, в которых записаны цифры сомножителей, можно подписывать буквами, обозначающими названия разрядов (рис. 47). Проводится черта, отделяющая сомножители

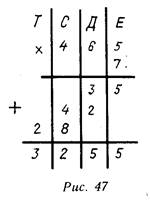
от произведения, ставится знак умножения «Х ». Затем учитель выполняет на доске умножение в столбик, поясняя свои действия: «Умножаем 5 число единиц в разряде единиц первого множителя на 7. Получаем 35. Записываем цифры этого числа в соответствующие клетки. Умножаем б десятков первого множителя на 7. Получаем 42 десятка (4 — число сотен, 2—-число десятков). Записываем 42 в следующую строчку, располагая цифры в соответствующих клетках; 4 сотни умножаем на 7, получаем 28 сотен (2—число тысяч, а 8 — число сотен в этом неполном

произведении). Записываем его в следующую строчку так, чтобы цифры располагались в соответствующих клетках. Полученные неполные произведения сложим: сначала в сумму запишем 5 единиц, сложим З десятка с двумя и запишем в разряд десятков...»

После этого учитель убеждает учащихся, что выполненное таким образом умножение отличается от ранее рассмотренного способа лишь формой. Поэтому произведение этих же чисел — 465 . 7

вычисляется в строчку:

Если необходимо, рассматривается еще один пример, однако подробные пояснения при этом в основном дают учащиеся.

Учитель предлагает сократить запись умножения в столбик. Это можно сделать, если запоминать некоторые промежуточные результаты, подобно тому как это делалось при сложении и вычитание в столбик. Образец краткой записи уместно показать на уже рассмотренном примере:

Учитель поясняет: «5 умножим на 7, получим 35; 5 записываем под единицами, а З десятка запоминаем; б десятков умножим на 7, получим 42 десятка и еще З десятка — всего 45 десятков; 5 записываем под десятками, а 4 сотни запоминаем; 4 умножим на 7 ...э. В дальнейшем учащиеся все с большей самостоятельностью работают над подобными вычислениями.

Особо следует рассмотреть случаи умножения, когда первый множитель имеет вид: 3 520, 372 400, 872 000 и т. д. При записи этих множителей в столбик приходится умножать однозначный множитель на нуль, причем иногда неоднократно. С помощью уже известного приема показывается, что однозначный множитель умножается не на все разрядные слагаемые, а только на нулевые. Например, вычисляя произведение 872 000 4, на 4 достаточно умножить число 872 и к полученному результату приписать справа три нуля:

В процессе отработки алгоритма умножения на однозначное число используются упражнения с составными именованными числами. Так же как и письменные операции сложения и вычитания, умножение в таких случаях выполняется двумя способами: без перевода единиц величин в более мелкие и с переводом. Первый способ используется для придания конкретного смысла промежуточным операциям алгоритма умножения. Например, при умножении 5 мм на 8 получается 40 мм, что составляет 4 сн; умножение 7 см на 8 дает 56 см, или 5 дм и б см и т. д.

Письменное умножение не должно использоваться учащимися бездумно, применительно к любому произведению многозначного и однозначного чисел. Параллельно с работой над сложными произведениями, которые нельзя вычислить устно, необходимо предусмотреть возможность для упражнения учащихся в устном счете. Для этого в систему упражнений могут включаться, например, такие произведения: 1020.5, 5203.2 и др.

Умножение числа на произведение. При изложении методики обучения учащихся правилам прибавления числа к сумме, суммы к числу и других подчеркивалось, что не следует их побуждать к заучиванию формулировок этих правил. Смысл правил раскрывается через текстовые задачи. Этого же принципа следует придерживаться при обучении учащихся умножению числа на произведение.

В качестве исходной может быть рассмотрена, например, такая содержательная задача, предполагающая практическую деятельность учащихся: «Отрезок длиной 2 клетки тетради нужно увеличить сначала в 3, а потом в 4 раза. Какую длину будет иметь полученный отрезок? Запиши выражение, выполни рисунок». Выясняется, что требуемый отрезок можно построить разными способами (рис. 48):

1) 2 . З . 4 строится отрезок в З раза больший данного, а затем полученный отрезок откладывается на прямой 4 раза (так, чтобы конец предыдущего совпадал с началом следующего);

2) 2.4.3 данный ‚отрезок откладывается на прямой 4 раза,

/ а затем полученный отрезок откладывается З раза;

3) 2 12 данный отрезок откладывается на прямой 12 раз.

Констатируется, что результат выполнения задания разными способами одинаков. Делается вывод, что (2 . 3) 4 = (2 . 4. 3 = = 2 . (4 . 3), т. е. произведение трех чисел можно вычислять в любом порядке.

Это правило иллюстрируется на примерах: «Вычисли произведение удобным способом: 16.5.2,20526, 13. 400.3, ...э Имея ввиду следующую тему, целесообразно решить несколько примеров такого вида: «Вычисли удобным способом: 26.2. 10, 10.4.23, 5•100• 16» и т. д.

Умножение многозначного числа на разрядные ч и с л а. Прежде всего с учащимися нужно вспомнить (во время устного счета, например), как умножить число на 10, 100 и 1000.

Затем в порядке возрастающей трудности предлагаются произведения, в которых один из множителей разрядное число (круглые десятки, сотни, единицы тысяч). Вначале алгоритм умножения таких чисел рассматривается подробно. Пусть нужно умножить 17 на 30; 30 это З десятка, т. е. 3. 10. Значит, 17 можно умножить на произведение 17 . (3. 10). Такое умножение можно выполнить разными способами. Если 17 сначала умножить на 10, то число 170 на З умно. жить трудно. Лучше умножить 17 на 3, получим 51. Это число легче умножается на 10, получаем 510.

Находятся еще несколько произведений, для которых вычисления производятся устно (26 20, 13 60, 17 40 и т. д.).

Аналогично выполняются устные вычисления в случаях, когда один из множителей — круглые сотни или единицы тысяч:

26.200=(26.2). 100=5200

13.600=(13.6)• 100=7800

37 . 2 000 = (37 . 2). 1 000 = = 74 000 и т. д.

Далее рассматриваются сложные случаи, когда устно умножить трудно (216 80, 456 . 400, 78 70, 4 657 . 40 и т. д.). Один из таких примеров решается в строчку:

78.70=(78.7).10=(78).10=5460

Х7

Более удобно такие числа умножать сразу в столбик. Так как умножение на 10, 100, 1 000 состоит в приписывании к числу справа

В случаях «а» и «б» учащиеся умеют удобно располагать множители, сносить нули в произведение. По аналогии выполняется запись множителей и в случае «в». В произведение сначала сносятся нули первого множителя (случай «а»), а затем нули второго множителя, (случай «б»). Выполняются упражнения на закрепление этого приема умножения.

Умножение многозначного числа на двузначное. Алгоритм умножения на двузначное число состоит из следующих операций: двузначный множитель представляется в виде суммы разрядных слагаемых; многозначное число умножается сначала на единицы разряда единиц, а затем на второе разрядное число.

Если сравнить алгоритмы умножения на круглые десятки и на двузначные числа, можно заметить между ними сходство:

563.30=563.(3. 10)=...

563.23=563.(2О+3)=...

В некоторых случаях оно еще большее:

267. 12=267.(2+ 10)=

267.20=267.(2. 10)=...

Поэтому можно предположить, что использование правила умножения числа на сумму для объяснения приема умножения на двузначные и трехзначные числа может вызвать у учащихся затруднения. Возможно, целесообразнее другой подход.

Пусть, например, объяснение умножения на двузначное число начинается с рассмотрения произведения 68. 12. По определению это произведение означает сумму из 12 слагаемых, каждое из которых

68. Как вычислить значение такой суммы? Могут быть рассмотрены различные способы: 68 4 + 68 8, 68 5 + 68 7, 68 3 + 68 9 и др.

Очевидно, что в приведенных случаях нужно дважды выполнить умножение в столбик и полученные результаты сложить. Только при вычислении суммы 68 . 2 + 68. 10 умножение в столбик нужно выполнить один раз: 68 2, 68 умножается на 10 устно. делается вывод:

чтобы умножить 68 на 12, удобно умножить на 10, 68 на 2 и полученные неполные произведения сложить в столбик. Этот вывод закрепляется при рассмотрении более сложного случая. Например, 68 35

сумму из 35 слагаемых — удобнее вычислить так: найти сумму ЗО слагаемых 68. 30; найти сумму 5 слагаемых 68 . 5; неполные произведения сложить.

Констатируется, что для умножения данного числа на двузначное нужно умножить данное число на десятки двузначного множителя, а затем на единицы. Вычисляя такие произведения в три приема, учащиеся убеждаются в трудоемкости работы:

далее используется методика обучения по образцу. Учитель записывает на доске более короткий вариант умножения на двузначное число.

68 Записи сопровождаются пояснениями: «Второй множитель записывается под первым так, чтобы разряды единиц 340 и десятков одного числа находить под соответствующие 204 ми разрядами другого. Умножаем 68 на 5, получаем первое неполное произведение 340. Умножаем 68 на 30, т. е.

68 умножаем на 3, но помним, что в результате получаются десятки. Чтобы не забыть об этом, будем записывать второе неполное произведение, начиная с разряда десятков, т. е. под цифрой 4 первого неполного произведения... Второе неполное произведение равно 204. Находим сумму неполных произведений, она равна 2 380».

Вычисление произведений, в которых первый множитель трехзначное или многозначное число, производится аналогично. Поэтому соответствующие примеры включаются в систему упражнений по данной теме без каких-либо разъяснений.

Особо рассматривается только случай, когда многозначный мно- житель оканчивается одним или несколькими нулями (6 700 . 27, 5 480.64, 77900.21 и т. д.). В случае возникновения у учащихся затруднений учитель напоминает им правила записи таких множителей в столбик и снесения нулей в произведение.

Умножение многозначного числа на трехзначное. Знакомство учащихся с этим алгоритмом также происходит с опорой на определение умножения. Что значит, например, умножить 352 на 246? Это значит, что нужно найти сумму 246 слагаемых, каждое из которых 352. Эту сумму легче вычислить так: найти сумму 200 слагаемых (352. 200), сорока слагаемых (352. 40), шести слагаемых (352. 6), полученные результаты сложить, т. е. 352. 246= =352. 200+352 40+352 6.

Учащиеся убеждаются, что значения каждого произведения они умеют вычислять в столбик, так же можно найти и сумму многозначных неполных произведений. Как и при изучении умножения на дву

Одновременно учащиеся упражняются в устном счете, в част:

ности в умножении многозначных чисел на однозначные, двузначные и трехзначные. для устного счета используются простые случаи умножения: 500 .600, 200 .30, 101 .40, 123. 3, 223.30, 323 .200.

При успешном изучении темы можно рассмотреть частные приемы устного умножения: 299 .4, 399. 50, 302 .31, 405. 11 и др. Умножение таких чисел основано на определении умножения. Так, произведение 299 . 4 можно заменить произведением 300 4, которое вычисляется устно. Первый множитель был увеличен на единицу. Поскольку 300 . 4 можно представить как сумму четырех слагаемых, каждое из которых увеличено на единицу, то, чтобы получить исходное произведение, нужно из 1 200 вычесть 4.

Умножение 302 на 31 можно мысленно представить как сумму, состоящую из 31 слагаемого. Удобно 302 . 30 = 9 060, т. е. найти сумму 30 слагаемых. Если к 9 060 прибавить тридцать первое слагаемое — .302, получим исходное произведение.

Деление. Определим, из каких операций состоит алгоритм. письменного деления (в дальнейшем будем называть его «деление углом»). Рассмотрим хорошо известный процесс деления углом на конкретном примере — 616 236:267 (самый сложный случай деления в начальных классах — деление многозначного числа на трехзначное).

Сначала выделяем неполное делимое 616. Подбираем цифру частного. Возможно, придется опробовать несколько цифр, прежде чем установим, что

это цифра 2. Умножаем делитель на 2, получаем

Вычитаем это произведение из неполного делимого. Разность равна 82. дополняем ее следую

Щей цифрой делимого, получаем неполное делимое 822. Подбираем следующую цифру частного — 3. Умножаем делитель на З и полученное произведение вычитаем из 822. дополняем разность следующей

цифрой делимого, получаем 213. Это неполное делимое не делится на 267, поэтому в частном записываем нуль. Сносим еще одну цифру делимого... и т. д. Отметим, что операция определения первого неполного делимого отличается от операции получения последующих неполных делимых.

Алгоритм можно представить в следующем виде:

1) определение первого неполного делимого;

2) определение цифры частного;

3) умножение делителя на подобранное число;

4) вычитание произведения из неполного делимого;

5) если цифра частного подобрана верно, то выполняется следующая операция алгоритма, если нет, повторно выполняются операции 3—5;

6) определяется неполное делимое. Если оно существует, выполняется третья и следующие за ней операции алгоритма. Если неполного делимого нет, деление окончено.

Приведенный алгоритм получен в результате анализа модели деятельности человека, хорошо знакомого с делением углом. Поэтому, возможно, здесь не отражены в явном виде операции, которые выполняются неосознанно. Поскольку этот алгоритм усваивается младшими школьниками, он нуждается в уточнении. Уточнять и дополнять этот алгоритм будем по мере усложнения случаев деления многозначных чисел. Заметим, что не все выделенные операции требуют специального изучения. Так, операция З изучена в теме «Умножение многозначного числа), операция 4 — в теме «Сложение и вычитание в пределах тысячи.

Изучение темы «деление многозначных чисел» естественно начать со случаев, когда делитель — однозначное число.

деление многозначного числа на однозначное (устное). Обучение делению многозначных чисел на однозначные начинается с самых простых случаев, когда каждое разрядное число делимого делится на делитель нацело: 248:2, 468:2, 639:3, 408:4 и т. д. Чтобы вычислить такое частное, не требуется алгоритма деления углом. Устно, начиная со старшего разряда, делятся разряд- ные числа, а получаемые промежуточные результаты записываются в соответствующие разряды частного.

Например, чтобы разделить 9 603 на 3, 9 тысяч делят на 3, получается З тысячи; б сотен делят на 3, получается 2 сотни; О десятков делят на 3, получается О десятков, З единицы делят на 3, получается единица. Таким образом, в частном З тысячи, 2 сотни, О десятков и одна единица. Значит, частное равно 3201.

Методика обучения этому приему следующая. Учащимся хорошо известен прием деления двузначных чисел на однозначные. Частные 36:3, 48:4, 63:3 вычисляются последовательным делением разрядных единиц. Этот прием учитель иллюстрирует на позиционном абаке, например, для частного 69:3 (рис. 49). Выполняется запись: 63:

:3=60:3+3:3. Затем наглядно можно представить прием деления в более сложном случае — 693 069:3. Этот процесс комментируется и описывается: 693069:3=600000:3+90000:3+ 3000.3+60:

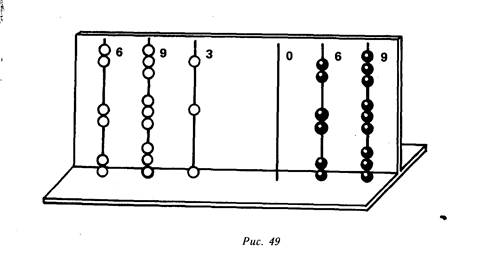
:3+9:З2ООООО+ЗОООО+1 000+20+3231 023. Правильность выполнения операции проверяется умножением. Подобные примеры учащиеся в состоянии выполнить без абака и промежуточных записей.

Поскольку рассмотренный прием устного деления многозначного числа на однозначное легко проиллюстрировать, нет необходимости в каких-либо математических обоснованиях (например, «доказательстве > правила деления суммы, состоящей из З и более слагаемых, на число). Излишним было бы и введение здесь специальной терминологии: «неполное делимое», «подбор цифры частного» и т. д., используемой в дальнейшем.

деление многозначного числа на однозначное (письменное). При изучении операции определения первого неполного делимого использует общий прием деления двузначного числа на однозначное. Чтобы вспомнить его, учащимся предлагается найти следующие частные: 81:3, 76:4, 65:5, 84:7, 91:7. Комментируя операцию деления, ученики воспроизводят содержание приема деления двузначного числа на однозначное: «Представим делимое суммой удобных слагаемых: одно из них самое большое число десятков, которое делится на делитель».

Затем рассматриваются более сложные частные. делимые в них — трехзначные числа, позволяющие использовать этот же прием деления: 920:2, 510:3, 840:3 и т. д. для первого частного такого вида преобразования можно выполнить письменно. Эта работа сопровождается, например, такими комментариями:

920:2 =

= (800 + 120):2 = Представим делимое суммой удобных слагаемых, одно из КО

ТОРЫХ — наибольшее число сотен, делящееся на делитель.

=800:2+120:2= делим оба слагаемых на делитель.

= 400 + 60 = 460 Складываем полученные частные. Правильность деления проверяется умножением. :3+9:З2ООООО+ЗОООО+1 000+20+3231 023. Правильность выполнения операции проверяется умножением. Подобные примеры учащиеся в состоянии выполнить без абака и промежуточных записей.

деление многозначного числа на однозначное (письменное). При изучении операции определения первого неполного делимого использует общий прием деления двузначного числа на однозначное. Чтобы вспомнить его, учащимся предагается найти следующие частные: 81:3, 76:4, 65:5, 84:7, 91:7. Комментируя операцию деления, ученики воспроизводят содержание приема деления двузначного числа на однозначное: «Представим делимое суммой удобных слагаемых: одно из них самое большое число десятков, которое делится на делитель».

920:2 =

= (800 + 120):2 = Представим делимое суммой удобных слагаемых, одно из КО

ТОРЫХ — наибольшее число сотен, делящееся на делитель.

=800:2+120:2= делим оба слагаемых на делитель.

= 400 + 60 = 460 Складываем полученные частные.

Правильность деления проверяется умножением.

В дальнейшем подобные примеры решаются устно.

После этого учитель приступает к объяснению деления трехзначных чисел.

Рис. дальнейшем подобные примеры решаются устно.

После этого учитель приступает к объяснению деления трехзначных

Приведем вариант пояснений к вычислению первого частного (цифра в скобках указывает порядковый номер операции алгоритма).

(1). Первое неполное делимое — 22.

(2). На 4 можно разделить 20, значит, первая цифра частного 5.

(3). Второе неполное делимое — 22 — 20 = 2, т. е. 2 десятка тысяч, или 20 тысяч, и еще б тысяч — 26.

(2). Из 26 на 4 можно разделить 24, значит, следующая цифра частного — 6.

(3). Найдем следующее неполное делимое — 26 — 24 = 2, осталось разделить 2 тысячи, или 20 сотен, и еще 8 сотен 28.

(2). 28 делится на 4, следующая цифра частного 7.

(3). Следующее неполное делимое — О десятков.

(2). 0 разделим на 4 и запишем в разряд десятков частного 0.

(3). Следующее неполное делимое — О единиц.

(2). 0 разделим на 4 и запишем в разряд единиц частного 0.

Ответ: 56 700.

После вычисления учащиеся могут догадаться», что нули делимого можно просто сносить в частное. В таком случае им предлагается, не выполняя деления, ответить, сколько нулей будет во втором частном (226 800:5). Вычислив это частное, ученики видят, что «догадка > неверна. Учитель объясняет, что для того чтобы не допускать ошибок при делении — не забывать записывать нули в частном и не записывать в частном лишние нули,— нужно заранее определять, сколько цифр имеет частное. Раскрывается содержание этой операции.

Например, для того чтобы узнать, сколько цифр в значении частного 226 800:5, определяется смысл первого неполного делимого. Число 22 означает в делимом десятки тысяч. При делении десятков тысяч в частном получаются десятки тысяч. Такие числа записываются с помощью пяти цифр. Значит, в частном будет пятизначное число. Можно посоветовать учащимся помечать места для цифр частного точками еще до начала деления.

На конкретных примерах ученики убеждаются в том, что определение количества цифр в частном полезно при любом делимом, а не только когда оно оканчивается нулями. Можно рассмотреть следующие частные: 7 371:7, 4 856:8, 45 063:9 и т. д. (Значения этих частных выражаются числом с одним или несколькими нулями в середине.) 4856 8 Пусть, например, 4 856 делится на 8. Первое неполное

56 Г607 делимое — 48, Оно означает количество сотен в делимом, значит, в частном будут получены сотни. Так как количество сотен записывается с помощью трех цифр, то значение частного будет трехзначным.

48:8=6, первая цифра частного—б.

Следующее неполное делимое — 5 десятков. Число 5 на 8 не делится, значит, в частном в разряде десятков нужно записать О (иначе

частном получится двузначное число), и т. д.

В дальнейшем при делении углом после выделения первого неполного делимого всегда выполняется операция определения количества цифр в частном.

Итак, в результате изучения письменного деления многозначного числа на однозначное учащиеся должны усвоить следующий алгоритм деления.

1. Определяется первое неполное делимое. В делимом, начиная со старшего разряда, выбирается такое наименьшее число, которое делится на делитель.

2. Определяется количество цифр в частном. Выясняется, какими разрядными единицами выражено первое неполное делимое. В частном получаются соответствующие разрядные единицы. В нем столько цифр, сколько необходимо для записи числа с данным количеством разрядов.

3. Определяется цифра частного. В неполном делимом выбирается наибольшее число, которое делится на делитель. Выполняется табличное деление.

4. Определяется неполное делимое. Вычисляется, сколько единиц осталось после деления предыдущего неполного делимого. К ним прибавляются единицы следующего разряда.

После операции 4 снова выполняется операция 3, и так до тех пор, пока можно будет образовывать неполные делимые.

Остановимся еще на нескольких методических особенностях изучения темы «Деление многозначного числа на однозначное».

Основой обучения математике в начальных классах являются текстовые задачи. Поэтому и при изучении алгоритма письменного деления учащимся часто приходится встречаться с частными, в которых компоненты представлены именованными и составными именованными числами. Наиболее часто деление в таких случаях выполняется так: сначала компоненты приводятся к одному наименованию, затем выполняется деление над отвлеченными числами: частное представляется в виде именованного или составного именованного числа.

Пусть, например, необходимо найти частное 24 р. 21 к.: З к:

Частное 807 именуется исходя из условия задачи.

Учащимся можно было бы предложить найти значение этого частного без предварительного перевода единиц. В таком случае операции алгоритма деления выполняются в несколько необычной ситуации, что, безусловно, полезно.

При изложении методики обучения делению в концентре <Сотня> отмечалось, что в житейских ситуациях деление с остатком приходится выполнять гораздо чаще, чем без остатка, Поэтому в систему упражнений по отработке приема деления целесообразно включать случаи деления с остатком. Это же требование распространяется и на систему упражнений по совершенствованию навыков деления углом.

Умение выполнять деление с остатком полезно еще в одном отношении. Известно, что при делении на двузначные и трехзначные числа особое значение имеет оценка промежуточных остатков. Если при делении неполного делимого остаток больше делителя, то соответствующая цифра частного подобрана неверно. Так, если при делении числа 345 678 на 7 получился остаток 18, учащихся легко убедить, что деление выполнено неверно: в частном должно получиться пятизначное число. Школьникам напоминается, что остатки при делении на число меньше делителя. Поэтому ошибку, допущенную при делении, можно обнаружить исходя из полученного остатка: 18 больше делителя, значит, 18 не может быть остатком:

Упражнение учащихся в делении с остатком целесообразно и для обобщения приема деления на 10 и 100. Этот прием будет использоваться в дальнейшем, при делении на двузначные и трехзначные числа.

Ученики знают, так разделить числа 80, 150, 1 300, 1 230 на