Вопросы и задания для самостоятельной работы 5 страница
Приведем фрагмент такого объяснения.
Уч ител ь: Сложи 356 и 227 на абаке. Прокомментируй выполняемые действия.
Ученик: К б прибавить 7—получим 13. 13 косточек составляют десяток и три единицы. На спице единиц оставляем З косточки, а снятые 10 косточек заменяем 1 косточкой, которую нанизываем на спицу десятка, и т. д.
Затем на абаке выполняется обратное действие: из 583 вычитается, например, 277. Из З вычесть 7 нельзя. Выход — в использовании правила замены 10 единиц десятком в обратном порядке. Теперь десяток заменяется 10 единицами. На спице единиц становится 13 косточек, зато на спице десятков — на 1 косточку меньше (рис. 43). Вначале промежуточное преобразование уменьшаемого можно записать. В дальнейшем оно выполняется в уме. Чтобы не забыть, что в старшем разряде была занята единица, над этим разрядом ставят точку

Затем изучается случай, когда в уменьшаемом занимается единица из разряда сотен. Решая первые примеры, учащиеся подробно комментируют выполняемые операции: «836—354. От б отнять 4, получится 2, 2 записываю в разряд единиц. От З отнять 5 нельзя. Занимаю от 8 одну сотню. Ставлю над 8 точку это значит, что осталось 7 сотен. Сотню дроблю на 10 десятков. От 13 десятков отнять 5, получится 8. Записываю 8 в разряд десятков. От 7 сотен отнять 3, получится 4 сотни. Записываю 4 в разряд сотен. Ответ:
В дальнейшем ученики лишь изредка, в случае затруднений, комментируют применение алгоритма, да и то в краткой форме:
От б отнять 4, получу 2. От З отнять 5 нельзя, занимаю сотню. От 13 отнять 5—8. От 7 отнять 3—4>.
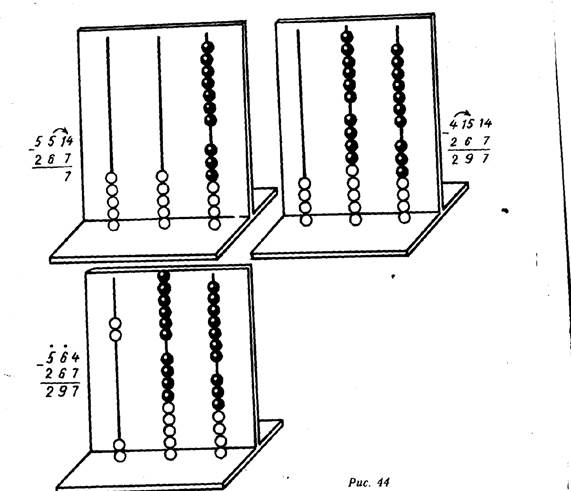
Подробно рассматривается случай, когда в двух разрядах уменьшаемого меньше единиц, чем в соответствующих разрядах вычитаемого: 564—267, 682—393, 407—149 и т. д.
Операции алгоритма иллюстрируются на демонстрационном абаке, на доске выполняются соответствующие математические записи (рис. 44). Используя опыт, приобретенный при изучении предыдущих случаев вычитания в столбик, учащиеся могут самостоятельно пояснить сущность и последовательность операций алгоритма. Содержание этих пояснений может, например, быть таким:
От 4 отнять 7 нельзя. Займем один десяток и раздробим его на 10 единиц. Всего стало 14 единиц. От 14 отнять 7, получится 7. Вычитаем десятки. От 5 отнять б нельзя. Займем одну сотню и раздробим ее на 10 десятков. Всего стало 15 десятков. От 15 отнять б, получим 9. От 4 сотен отнять 2 сотни, получим 2 сотни. Ответ: 297>.
Затем прием отрабатывается без выполнения промежуточных
записей. Если возникают затруднения, от учащихся можно потребовать прокомментировать выполняемые вычисления с помощью абака.
Учителю необходимо подробно остановиться еще на одном случае вычитания, когда недостающие в уменьшаемом единицы нельзя
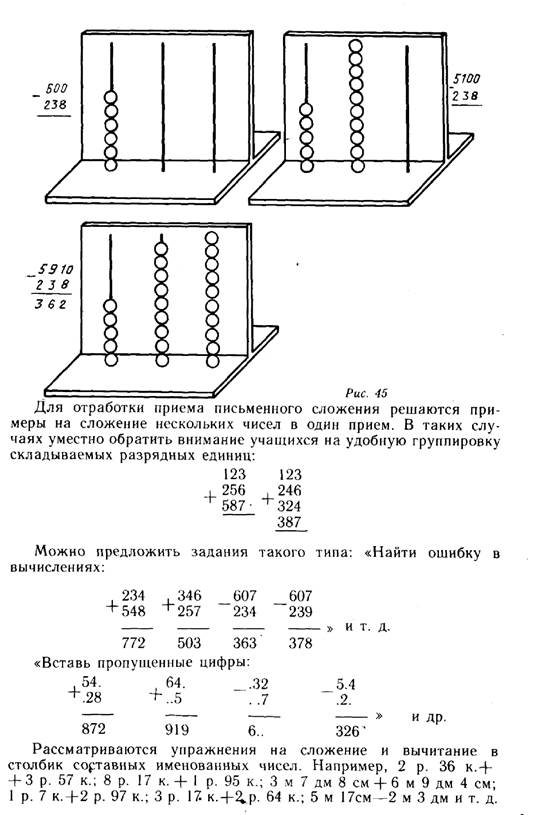
занять из соседнего разряда: 307—189, 600—231 и т. д. Под
руководством учителя учащиеся ВЫПОЛНЯЮТ операции на демонстрационном абаке (и индивидуальных абаках), математически записывают промежуточные действия и дают соответствующие пояснения (рис. 45). После выяснения особенностей этого приема следует особо оговорить оформление записи в столбик, когда промежуточные действия выполняются в уме. учащимся может быть предложен, например, такой вариант записи:
.9
По мере усвоения школьниками новых случаев упражнения на письменное сложение и вычитание разнообразятся. Так, ученикам предлагается выполнять проверку вычисленного результата с по- мощью обратного действия. Вычисляются значения выражений, содержащих несколько действий сложения и вычитания.
Операции над именованными числами выполняются после перевода обоих компонентов в более мелкие единицы. Однако нужно практиковать сложение и вычитание в столбик и без перевода. Это позволит учащимся наглядно представить понятие «разрядные единицы». Так, в данном случае единицы разряда единиц — это сантиметры, единицы разряда десятков дециметры, единицы разряда сотен метры:
м 7 дм 8 см
б м 9 дм 4 см
10 м 7 дм 2см
(Учащиеся незаметно для себя получили число больше тысячи. Это, конечно, полезно, если иметь в виду изучение в дальнейшем операций над многозначными числами.)
Одновременно с совершенствованием навыков письменного сложения и вычитания ученики должны закреплять вычислительные навыки, приобретенные при изучении предыдущих концентров. Это относится к приемам устного сложения и вычитания. Выше было показано, как организовать такую работу при изучении трехзначных чисел. Учащихся полезно побуждать к использованию правил прибавления числа к сумме и суммы к числу, вычитания числа из суммы и суммы из числа, облегчающих вычисления. Например:
(385+ 37) +63,885— (135+ 257), 126+253+344+ 207 и т. д. Такие упражнения могут выполняться устно.
7. МНОГОЗНАЧНЫЕ ЧИСЛА
Общие положения. Изучая материал концентров «десяток», “Сотня», «Тысяча», учащиеся ознакомились с цифрами десятичной системы счисления, разрядами единиц, десятков, сотен. Сейчас же им предстоит усвоить понятие классов чисел. Это понятие позволяет перейти к нумерации сколь угодно больших натуральных чисел. Поэтому в ко те«Мнщiыыаiкла» заканчивается изучение н ме а ни целых не т и ате предыдущих концентрах учащиеся запоминали таблицу сложения (вычитания), умножения (деления), овладевает устного выполнения эти операций, приемами письменного сложения и вычитания. В концентре Многозначные числа» эти знания и умения обобщаются для компонентов,, имеющих более трех цифр. Здесь же ученики овладевают алгоритмами письменного умножения и деления самыми сложными в конце математики начальной
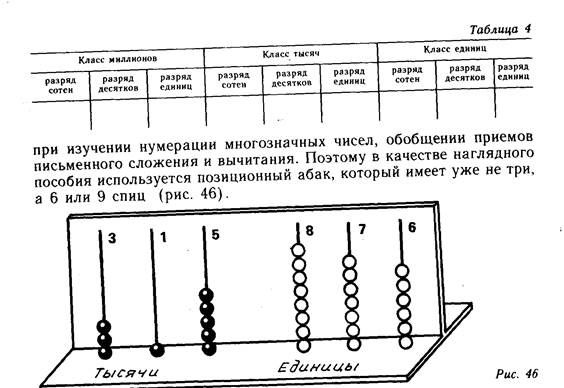
Нумерация и сравнение. При изучении нумерации многозначных чисел удобно использовать нумерационную таблицу, которая заполняется карточками с цифрами (табл. 4). Отметим, что в соответствии с программой 1986 г. нумерация изучается в пределах миллиона.
Возможно, что некоторые учащиеся встретятся с трудностями
Изучение нумерации многозначных чисел следует предварить
краткой, но яркой беседой о значении больших чисел. Материал для
такой беседы учитель может почерпнуть из справочников по промышленному и сельскохозяйственному развитию нашей страны, стран СЭВ, газетных и журнальных статей и т. д. Нужно показать учащимся, что без использования таких больших чисел, как миллион, сотни тысяч, невозможно выразить количество той или иной прОдуКi-1ии, выпускаемой нашими заводами, производимой в колхозах и совхоза х.
Переходя к изучению нумерации, необходимо вспомнить некоторые свойства позиционной системы счисления:
1) значение цифры в числе определяется ее местом в этом числе;
2) названия чисел, обозначаемых Одной, двумя и тремя цифрами, образуются по определенным правил ам;
3) прибавление к 9 единицам еще одной единицы данного разряда дает единицу следующего, более старшего разряда.
Для этого учащимся предлагаются например, такие упражнения (для устного счета).
1. Что означает цифра 3(5, 7) в числах 537; 735; 375? Сколько единиц каждого разряда в числах 573; 872, 670 и т. д.?
Сколько сотен, десятков, единиц в числах 674; 609; 70 и т. д.?
Какое число содержит б сотен; 8 десятков; 54 десятка; 2 сотни, б десятков и 4 единицы; 2 сотни и 8 единиц и т. д.?
return false">ссылка скрытаВ виде суммы каких разрядных слагаемых можно представить числа 823; 321; 149, 303 и т. д.?
2.длина отрезка 15 мм. Как по-другому можно выразить его длину? Как можно выразить длину отрезка в 206 см; 29 дм; 400 см; 400 дм и т. д.?
Как называется число, в котором 10 десятков; 10 сотен; 60 десятков и т. д.?
3. К 9 единицам прибавили единицу; к 8 десяткам прибавили 2 десятка; к 4 сотням прибавили б сотен и Т 1 Как наТяют При изучении нумерации многозначных чисел можно выделить два Сначала учащиеся учатся называть и записывать многотичные числа, не имеющие единиц в разрядах класса единиц, т. е. числа, оканчивающиеся тремя нулями. Вспомним, как начиналось знакомство учащихся с нумерацией чисел в пределах 100, 1000. Рассматривались соответственно понятия «десяток», «сотня», Десяток и сотня использовались затем как счетные единицы.
Первые числа класса тысяч образуются в результате счета тысячами: одна тысяча, две тысячи десять тысяч. Одновременно заполняется косточками спица тысяч абака. При получении 10 тысяч, согласно правилу работы с абаком, десять косточек на спице
тысяч заменяются одной косточкой на спице более старшего разряда — десятков тысяч.
Далее счет продолжается уже десятками тысяч: десять тысяч, двадцать тысяч сто тысяч. На соответствующую спицу абака последовательно нанизываются косточки. Когда их оказывается десять, они заменяются одной косточкой, которая нанизывается на спицу более старшего разряда —- сотен тысяч.
Затем учащиеся считают сотнями тысяч. Одновременно заполняется соответствующая спица абака. Как только на ней появляется 10 косточек, все они заменяются одной косточкой на следующей спице. Число, которое эта косточка обозначает, называется миллионом.
Таким образом, ученики знакомятся с названиями новых разрядов единиц тысяч, десятков и сотен тысяч и учатся заполнять соответствующие спицы абака.
Далее учащиеся учатся называть числа вида 11 тысяч, 24 тысячи, 347 тысяч и т. д. Для этого используются следующие упражнения. На спицы единиц, десятков и. сотен тысяч абака нанизаны соответственно 5, 3 и 7 косточек. Спрашивается, какое число изображено на абаке. Учащиеся рассуждают: в этом числе 7 сотен тысяч, З десятка тысяч и 5 тысяч. Учитель объявляет, что такое число называется семьсот тридцать пять тысяч.
Одновременно учащиеся работают над упражнениями другого рода: называется число, обозначающее некоторое количество тысяч, нужно отложить соответствующее количество косточек на спицах абака.
В процессе такой работы школьники должны увидеть сходство в образовании названий чисел первого и второго класса: для единиц тысяч не существует специальных названий, они называются так же, как единицы первого класса, но с прибавлением слова «тысяча»; нет специальных названий и для десятков тысяч: для них используются названия десятков первого класса с прибавлением слова «тысяча» и т. д.
Для закрепления этих знаний может быть составлена, например, следующая таблица:

Вместе с тем важно показать различие между одноименными разрядами классов единиц и тысяч. Для этого на абаке откладываются, например, числа: 120 тысяч и 120, 50 тысяч и 50, 178 тысяч и 178. Обсуждается сходство и различие в изображении этих чисел. Сходство состоит в том, что на спицах соответствующих разрядов класса единиц и тысяч отложены одинаковые количества косточек. Однако 8 косточек для числа 178 означает количество единиц в разряде единиц, а для числа 178 тысяч количество тысяч в разряде единиц тысяч.
Далее учащиеся записывают многозначные числа, оканчивающиеся тремя нулями. В изображении числа 5 тысяч на абаке в младших разрядах отсутствуют косточки. Это означает, что в этих разрядах О единиц. Обозначение этого числа цифрами выполняется в нумерационной таблице. В связи с.использованием этой таблицы вводится понятие класс», еще раз обсуждается сходство и различие в значении разрядов разных классов.
После заполнения абака и таблицы учащиеся записывают данное число в тетрадях. Для удобства записи многозначного числа между группами цифр разных классов оставляется промежуток (например, клетка тетради).
Аналогично приходят к записи чисел вида 700 тысяч, 107 тысяч, 420 тысяч, 567 тысяч и т. д. Основным средством наглядности при этом является нумерационная таблица.
г Одновременно с изучением нумерации можно рассмотреть приемы устного сложения и вычитания многозначных чисел. Эти приемы основаны на знании учащимися разрядного состава многозначных чисел и применимы лишь в случаях следующего вида: 200000+
+ 300 000, 100 000 + 50 000+7 000, 600 000—400 000, 350 000—
—50 000, 342 000—42 000 и т. д. Вычисления при необходимости легко иллюстрируются с помощью абака и нумерационной таблицы. Устное вычисление значений таких выражений способствует усвоению нумерации и подготавливает учащихся к выполнению письменного сложения и вычитания многозначных чисел.
Умножение и деление вида 5000. 2, 80 000:4, 17000. 3,
150 000:5 не требует специального приема и целиком опирается на
знание учащимися названий соответствующих многозначных чисел
и таблицы умножения и деления, приемов устного умножения и деления.
Вместе с тем эпизодическое решение таких примеров облегчает усвоение нумерации, изучение последующих тем, связанных с умножением многозначных чисел.
С нумерацией остальных многозначных чисел учащихся можно ознакомить в процессе прибавления к многозначным числам, оканчивающимся тремя нулями, чисёл первого класса. На абаке откладывается многозначное число уже известного учащимся вида, например 315 000. На спицы разрядов первого класса нанизываются косточки, соответствующие числу, например 876 (см. рис. 46). Учитель спра4iiивае, как записать число, получившееся в результате сложения 315000 и 876. Ответ очевиден. Подобны
числа демонстрируются на нумерационной таблице. Учащиеся учатся называть подобные числа: сначала называется число единиц второго класса, а затем первого класса. Таким образом, число 315 876 читается так: триста пятнадцать тысяч восемьсот семьдесят шесть.
Предлагаются и обратные упражнения: по названию числа выполнить его запись (возможно, с предварительным изображением его на абаке).
В связи с введением понятия класса в систему упражнений по отработке навыков устной и письменной нумерации целесообразно включать упражнения, требующие использования этого понятия. Это могут быть, например, такие Задания: «Запишите (изобразите на своем абаке) число, в котором: 200 единиц первого класса и 60 единиц второго класса; 107 единиц класса единиц и б единиц класса тысяч; по две единицы в разряде десятков второго класса и в разряде сотен первого класса; 320 единиц класса тысяч и 2 единицы класса единиц» и т. д.
Наряду с такими упражнениями предлагаются и обратные:
«Назови, к какому классу и разряду относится каждая цифра числа 356 789, 50 283 и т. д.».
Изучая нумерацию, учащиеся продолжают упражняться в устных вычислениях (сложении и вычитании) на множестве многозначных чисел: 350 000+102, 200 018+600 100, 85007—80007, 150 120—50 100 и т. д.
Для расширенного множества чисел устанавливается справедливость отношения порядка. Учащиеся считают в прямом и обратном порядке, начиная с определенного числа; определяют числа, следующие непосредственно до и после данного числа. Например, им предлагается продолжить счет с 998 до 1005, с 7 589 до 7 600; присчитывать по единице к числам 99 989, 999 997; отсчитывать по одному от чисел 600000, 100000, 10000, 7000; назвать число, которое на 2 меньше, чем 40 000, и т. д.
Школьники должны научиться сравнивать многозначные числа. С помощью позиционной таблицы легко показать, что начинать сравнивать два многозначных числа нужно с единиц второго класса. То число больше, у которого больше единиц второго класса. Если их число одинаково, то сравнивается число единиц первого класса.
Увеличение и уменьшение числавi0, IОО и IООО раз. Расширяя знания учащихся о десятичной системе счисления, можно ознакомить их с простым способом увеличения или уменьшения числа в 10, 100 и 1 000 раз, кратного сравнения чисел особого вида. Это необходимо для прочного усвоения ими позиционного принципа нумерации. Изложим методику изучения этого материала.
Учащимся предлагают рассмотреть ряд чисел и рассказать об их особенностях. Пусть этот ряд имеет вид: 3, 30, 300, 3 000, 30 000, 300 000. В числе обнаруженных особенностей могут быть такие: в каждом числе встречается цифра 3; все числа записаны с помощью одной цифры З или цифры З и нулей; цифра З в каждом числе обозначает разные разрядные единицы: единицы, десятки, сотни и т. д.
Предлагается последовательно сравнить эти числа парами.
Зи 30: ЗОн 10 раз больше, чем З, так как 30:3= 10 (это учащимся известно из темы «Увеличение и уменьшение числа в несколько раз»);
ЗО и ЗОО: эти числа можно представить в виде З десятка и ЗО десятков; это позволит, как и в предыдущем случае, установить, что ЗО десятков в 10 раз больше, чем З десятка, а значит, ЗОО в 10 раз больше, чем ЗО.
Аналогично устанавливается соотношение между парами ЗОО и
3 000, 3 000 и 30 000, 30 000 и 300 000.
далее сравниваются числа З и 300. Случай 300:3 рассматривался
уже в концентре «Тысяча» — 300:3 = 100. А это,
как известно, означает, что 300 в 100. раз больше, чем З. Такие же
соотношения устанавливаются и для чисел ЗО и 3 000, 300 и 30 000,
3 000 и 300 000 (для этого они приводятся к виду З дес. и 300 дес.,
З сот. и 300 сот. и т. д.).
Вывод о том, что 3 000 в 1 000 раз больше, чем 3, делается по индукции. Этот вывод распространяется и на другие пары чисел.
Затем следует обобщение: число, которое в 10 (100, 1 000) раз больше другого, имеет на один (два, три) нуль справа больше. На основании этого вывода делается заключение, что если у числа на один
(два, три) нуль справа меньше, чем у другого числа, то оно в 10 (100 или 1 000) раз меньше другого числа.
Выполняются упражнения на закрепление: «Увеличь число 5 в 10, 100, 1 000 раз; число 80 — в 10, 100, 1 000 раз» и т. д.; «Уменьши
число 300 в 10, 100 раз; число 70000 в 10, 100, 1 000 раз» и т. д. Эти правила без каких-либо пояснений можно использовать для
сравнения чисел 118 и 1180, 27 и 27000 и т. д.
Состав многозначных чисел. С целью подготовки учащихся к изучению алгоритмов письменного умножения и деления полезно научить их определять, сколько полных десятков, сотен,
тысяч содержится в данном многозначном числе.
Ученики обладают некоторым опытом выполнения заданий такого рода: они умеют определять, сколько десятков в трехзначном чис- ле. Это и используется в работе с многозначными числами.
Школьникам предлагается определить, сколько десятков в числе 3 576. Это число представляетсй в виде суммы разрядных слагаемых.
7 Последовательно выясняется, сколько десятков в каждом из
60 этих слагаемых: 7, 50, 300. (Например, учащиеся рассуждают так; в 1000—10 сотен или 100 десятков, значит, в 3000----З00 десятков.) В числе 3 576—357 десятков. Аналогично устанавливается, что в этом числе 35 сотен. Если рассмотреть столь же
подробно еще несколько чисел, то нетрудно заметить закономерность в определении состава числа.
И ме н о в а н н ы е ч ис л а. Большую помощь при изучении и усвоении нумерации многозначных чисел оказывают упражнения с составными именованными числами, выраженными в десятичных мерах. Эти числа дают возможность наглядно представить понятия разряда тысяч, десятков и сотен тысяч. Такие упражнения должны использоваться на всех этапах изучения нумерации. Например, когда учащиеся учатся определять состав многозначного числа, целесообразно выполнить такие упражнения: «Сколько дециметров в 3 576 см? Сколько километров составляют 3 576 м? Сколько килограммов в 12 070 г? Сколько рублей составляют 67 000 к?» и т. д. Основные положения методики обучения нумерации в пределах миллиона могут быть использованы и для знакомства учащихся с числами класса миллионов.
Сложение и вычитание (письменные вычисления). При изучении многозначных чисел учащиеся устно складывают и вычитают числа особого вида, используя знание разрядного состава чисел, т. е. многозначных чисел, которые можно представить в виде двузначных и трехзначных именованных чисел (38 000 + 27 000 — 38 тыс. + 27 тыс., 620 000 — 370 000 — 62 дес. тыс.— 37 дес. тыс, и т. д.). Перед тем как обратиться к приемам письменного сложения и вычитания, ученикам целесообразно поупражняться в решении таких примеров. Алгоритмы письменного сложения и вычитания одинаковы и когда компоненты являются трехзначными числами, и когда они — многозначные числа. Правда, если уменьшаемое и вычитаемое — трехзначные числа, то приходится образовывать или дробить разрядные единицы не более двух раз. Если же компоненты — многозначные числа, то эти операции могут использоваться большее число раз. Поэтому задача учителя состоит в том, чтобы показать учащимся, что известные алгоритмы письменного сложения и вычитания применимы к числам нового вида. Это можно сделать по-разному.
Например, учитель предлагает учащимся систему последователь но усложняющихся сумм и разностей:

Объяснить учащимся, как вычисляются эти примеры, легко, поскольку в каждом случае компоненты можно представить как трехзначные именованные числа, например 756 тыс. + 243 тыс.
Затем ученики складывают и вычитают числа, которые не оканчиваются нулями, но без перехода через десяток и без дробления разрядных единиц.
Перед тем как приступить к изучению более сложных случаев (с образованием новых разрядных единиц и дроблением разрядных единиц на более мелкие), полезно упражнение учащихся в многократном выполнении этих операций.
Например, рассматривается случай прибавления единицы к числу 99 999. Учащиеся знают, что за этим числом следует число 100 000. Однако на абаке или нумерационной таблице подробно рассматривается механизм образования суммы: к 9 единицам прибавить один, получим десяток; в разряд единиц записываем 0, а получившийся десяток прибавляем к 9 десяткам; получаем 10 десятков, или 100; в разряд десятков записываем О и т. д.
Так же подробно можно проследить процесс вычитания единицы из числа 100 000. При этом в записи используются обычные обозначения заема и распределения разрядных единиц (точки и девятки):



При вычислении суммы или разности более высокого уровня сложности от учащихся следует требовать подробных пояснений к выполняемым промежуточным операциям. Например, вычисление разности одного из самых сложных видов — 600 007 — 532 468 учащихся сопровождают следующими объяснениями: «От 7 отнять 8 нельзя. Занять единицы можно только в разряде сотен тысяч. Возьмем одну сотню тысяч (поставим над б точку) и раздробим ее на 10 десятков тысяч. Возьмем десяток тысяч (над разрядом единиц тысяч запишем 9) и раздробим ее на 10 сотен...» и т. д. Соответствующая запись имеет вид:

В дальнейшем время от времени от учащихся требуются краткие комментарии к выполняемым операциям.
Приемы письменного выполнения действий с многозначными числами в основном не отличаются от приемов выполнения этих действий над трехзначными числами. Однако учитель должен иметь в виду, что обилие промежуточных операций может на первых порах вызвать у учеников затруднения. Поэтому при необходимости эти приемы следует проиллюстрировать на абаке.
Сложение и вычитание именованных чисел. Важную роль в теме «Сложение и вычитание многозначных чисел» играют составные именованные числа. Здесь можно использовать опыт работы с такими числами, приобретенный учащимися в концентре <Тысяча». Отметим только, что в дальнейшем особую роль могут играть упражнения с составными именованными числами, выраженными в единицах времени. Они позволят проверить уровень понимания учащимися сути приемов письменного сложения и вычитания. В самом деле, эти приемы будут использоваться в принципиально новых условиях (компоненты выражены в недесятичной системе счисления):

Умножение. На практике письменное умножение и деление изучаются во взаимосвязи. В самом деле, изучение алгоритма письменного умножения на однозначное число открывает возможности для изучения приема письменного деления на однозначный делитель. То же можно сказать и об умножении и делении на двузначные и трехзначные числа. Здесь для удобства методика письменного умножения будет рассматриваться отдельно. Прежде чем обратиться непосредственно к методике обучения учащихся умножению в столбик, выполним дидактический анализ соответствующего алгоритма.
Начнем с конечного результата изучения умножения: учащиеся должны уметь умножать многозначные числа на трехзначные. На конкретном примере вспомним, в чем состоит это умение.

Вначале оба множителя правильно записываются друг под другом. Затем число, стоящее в разряде единиц второго множителя, умножается на многозначный множитель,
начиная с наименьшего разряда. Полученный результат правильно записывается под чертой, отделяющей множители от произведения.
На многозначный множитель умножаются единицы разряда десятков второго множителя. Результат правильно записывается под первым неполным произведением. Наконец, на многозначное число умножаются единицы разряда сотен второго множителя, а результат правильно записывается под вторым неполным произведением. Полученные неполные произведения складываются. Сумма и есть значение произведения 4 345 и 276.
Пока оставим вопрос о том, что значит правильно выполнять записи при умножении в столбик. Очевидно, что расположение записей сказывается на правильности получаемого результата. Выделим только те операции алгоритма, которые связаны с выполнением арифметических действий:
1) многозначное число умножается на однозначное;
2) многозначное число умножается на круглые десятки;
3) многозначное число умножается на круглые сотни;
4) три многозначных числа складываются.
Операция 4 известна учащимся из темы «Сложение и вычитание многозначных чисел», поэтому предметом специального изучения должны стать операции 1—3. Остановимся подробнее на их содерж а нии.
Умножение многозначного числа на однозначное имеет много общего с приемом умножения двузначного числа на однозначное:
многозначный множитель представляется в виде суммы разрядных слагаемых, и эта сумма по специальному правилу умножается на однозначный множитель (543 4 = (500 + 40 + 3). 4). Вместе с тем между этими приемами есть и различие. Так, при умножении многозначных чисел сумма разрядных слагаемых может иметь 3, 4, 5 и даже б слагаемых; на однозначное число умножаются круглые сотни, тысячи, десятки и сотни тысяч; полученные многозначные неполные произведения нелегко сложить в уме.
Итак, для усвоения операции 1 учащиеся должны научиться умножать на число сумму, состоящую из 3,4, 5 и б слагаемых, и умножать на однозначное число многозначные разрядные числа.
Чтобы научить учащихся выполнять операцию 2, нужно либо придумать наглядную иллюстрацию умножения числа на круглые десятки, либо свести этот случай к ранее изученным с помощью специального приема. Второй путь проще. В самом деле, при изучении нумерации многозначных чисел было показано, как увеличить (уменьшить) число в 10, 100 и 1 000 раз. Круглые десятки (сотни) можно представить в виде произведения однозначного числа на 10. Таким образом, выражение 543. 30 можно представить в виде 543 . (3. 10). Для того чтобы учащиеся могли выполнить такое ум ножение, им нужно показать, что умножить число на произведение можно разными способами (в частности, 543 3. 10). Для умножения 543 на З используется операция 1.
Аналогично можно обучить учащихся выполнению операции 3. Итак, разработана стратегия обучения учащихся алгоритму умножения в столбик. Она состоит в последовательном изучении следующих тем.
1. Обобщение правила умножения суммы на число для случаев, когда сумма имеет более двух слагаемых.
2. Умножение разрядных чисел второго класса на однозначное число.
3. Умножение многозначного числа на однозначное.
4. Правило умножения числа на произведение.
5. Умножение многозначного числа на круглые десятки и сотни.
6. Умножение многозначного числа на двузначное.
7. Умножение многозначного числа на трехзначное.
Рассмотрим методику изучения этих тем.
Правило умножения суммы на число. Учащимся предлагается следующая задача: «Для уроков труда было куплено З набора. В каждый набор входила линейка ценой 25 к., угольник за 20 к., циркуль ценой 22 к. и набор фломастеров за З р. Сколько стоили купленные наборы?»
По задаче составляется выражение: (25 + 20 + 22 + 300). 3. Обсуждаются способы вычисления этого произведения: «Если сначала найти стоимость одного комплекта, то получится трехзначное число 367, которое умножить на З трудно. Ответ можно найти и по-другому:
«Узнаем, сколько стоят в отдельности линейки, циркули, угольники и фломастеры. Полученные стоимости сложим. Значит, нужно найти значение выражения: 25 3 + 20 3 + 22 3 + 300. 3». Каждое из произведений учащиеся в состоянии вычислить устно, сумма 900 + + 67 также находится устно. При решении такой задачи у учащихся не должно возникнуть вопроса о правомерности умножения суммы четырех слагаемых на число почленно. Рассматриваемая в задаче ситуация проста и естественна. При необходимости можно рассмотреть аналогичную задачу, в которой на число умножается сумма, состоящая из З или 5 слагаемых. В заключение можно сформулировать правило умножения числа на сумму, однако требовать от учеников его запоминания не следует.