Локальная интерполяция

 

Однако, интерполяция при большом числе узлов приводит к необходимости работать с многочленами высокой степени (например, 50-й или даже 100-й), что неприемлемо как с точки зрения вычислений, так и из-за склонности таких многочленов к осцилляции (колебаниям) между узлами сетки. Поэтому на практике часто используют интерполяцию кусочными многочленами (или локальную интерполяцию).

При этом между различными узлами выбираются различные многочлены невысокой степени.

Линейная интерполяция – интерполяция алгебраическим двучленом f(x)=ax+b функции f, заданной в двух точках x₀ и x₁ отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

Интерполяция сплайнами – это быстрый, эффективный и устойчивый способ интерполяции функций. Наравне с рациональной интерполяцией, сплайн-интерполяция является одной из альтернатив полиномиальной интерполяции. Обычно применяют интерполяцию сплайнами, представляющими собой параболы 2-го и 3-го порядка

В основе сплайн-интерполяции лежит следующий принцип. Интервал интерполяции разбивается на небольшие отрезки, на каждом из которых функция задается полиномом третьей степени. Коэффициенты полинома подбираются таким образом, чтобы выполнялись определенные условия (какие именно, зависит от способа интерполяции). Общие для всех типов сплайнов третьего порядка требования – непрерывность функции и, разумеется, прохождение через предписанные ей точки. Дополнительными требованиями могут быть линейность функции между узлами, непрерывность высших производных и т.д.

Основными достоинствами сплайн-интерполяции являются её устойчивость и малая трудоемкость. Системы линейных уравнений, которые требуется решать для построения сплайнов, очень хорошо обусловлены, что позволяет получать коэффициенты полиномов с высокой точностью. В результате даже про очень больших N (числе экспериментальных точек) вычислительная схема не теряет устойчивость.

Сплайны в машиностроительном черчении и математике применяются .уже давно, так как сплайн – это не что иное, как гибкая линейка, которую деформируют так, чтобы по ней можно было провести кривую через заданные точки (х_i, y_j). Будучи деформирована таким образом, линейка приобретает форму, при которой запасенная в ней упругая энергия минимальна. Используя теорию изгиба бруса при малых деформациях, можно строго показать, что сплайн – это группа сопряженных кубических многочленов, в местах сопряжения которых первая и вторая производные непрерывны. Такие функции называют кубическими сплайнами. Чтобы построить кубический сплайн, необходимо задать коэффициенты, которые единственным образом определяют кубический многочлен в промежутке между данными точками. Например, в случае, представленном на //, необходимо задать все кубические функции q₁(x), q₂(x), . . ., q_n(x). В наиболее общем случае эти многочлены имеют вид

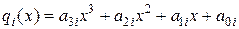, i=1,2, , n,

где a_ji – постоянные удовлетворяющие условиям на границах сплайнов.

Первые 2n условий требуют, чтобы сплайны соприкасались в заданных точках. Эти условия имеют вид

i=1,2, , n

i=1,2, , n-1

Следующие 2m-2 условий требуют, чтобы в местах соприкосновения сплайнов были равны первые и вторые производные:

, i=1,2, , n-1

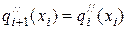, i=1,2, , n-1

Чтобы система алгебраических уравнений имела решение, необходимо, чтобы число уравнений точно равнялось числу неизвестных. На данном этапе мы имеем 4m неизвестных и 4m-2 уравнений. Следовательно, мы должны найти еще два уравнения. Обычно используют уравнения

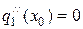и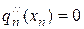

Полученный таким способом сплайн называют «естественным кубическим сплайном». Найдя коэффициенты сплайна, можно использовать эту кусочно-гладкую полиномиальную функцию для представления данных при интерполяции, подгонке кривой или поверхности.

Следовательно, определение коэффициентов сводится к решению 4m уравнений с 4m неизвестными. Число определяемых коэффициентов равно числу заданных точек. Поэтому решение оказывается не более сложным, чем в случае аппроксимации n+1 точек многочленом n-ой степени. Часто оказывается, что кубический сплайн аппроксимирует функцию лучше, чем многочлен степени n. Следует отметить, что существуют и другие сплайны, получающиеся при других условиях на концах или использовании многочленов более высоких степеней.