Базовые алгоритмы

Для реализации циклических вычислительных процессов часто используются следующие базовые алгоритмы:

• табулирование функций;

• организация счетчика;

• накопление суммы или произведения;

• поиск минимального или максимального члена последо­вательности.

Ниже приводятся примеры программирования задач на осно­ве базовых алгоритмов.

Задача 1. Алгоритм организации счетчика

Дана последовательность:

cos 1, cos 3, cos 5, ..., cos 99.

Определить количество положительных членов последова­тельности.

Решение

Представим последовательность в общем виде:

а = cos(2n -1), где п = .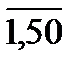

Для организации счетчика в памяти компьютера выделяется ячейка, содержимое которой должно увеличиваться на 1 каждый раз, когда встречается положительный член последовательности. В программе ячейке (счетчику) соответствует переменная целого типа, например переменная L. Работа счетчика реализуется с по­мощью оператора присваивания L=L+1. В начальный момент содержимое ячейки должно быть равно нулю. С этой целью пред­варительно осуществляется очистка ячейки оператором присваи­вания L=0.

 

#include "stdafx.h"

#include<math.h>

int main()

{

float a;

int n,L; // описание переменных

L=0; // очистка счетчика

for(n=1;n<=50;n++) //запуск цикла

{

a = cos(2*n – 1.0); // тело цикла

if(a>0) L = L + 1; // тело цикла

}

printf("L=%d", L); // вывод значения счетчика

return 0;

}

 

Задача 2. Алгоритм накопления суммы

Дана последовательность:

sin 2x, sin 4x, sin 6x, ..., sin l6x

x - заданное вещественное число.

Вычислить сумму членов последовательности, которые по модулю больше 0.3.

Решение

Общий член последовательности имеет вид:

а = sin(2nx), где n = .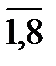

Для вычисления суммы в памяти компьютера выделяется ячейка S, к содержимому которой прибавляется член последовательности а каждый раз, когда выполняется условие 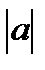> 0.3. Накопление суммы реализуется оператором присваивания S=S+a;. В начальный момент ячейка для суммирования должна быть очищена оператором S=0;.

#include "stdafx.h"

#include<math.h>

int main()

{

float a, x, S; //описание переменных задачи

int n;

printf("Введите значение х= ");

scanf("%f",&x);

S=0;//очистка суммы

for(n=1;n<=8;n++)// запуск цикла

{

a=sin(2*n*x);

if ( abs(a)>0.3) S = S + a;/* добавление числа а в сумму, если |a|>0.3 */

}

printf("S=%6.2f",S); // вывод значения суммы на экран

return 0;

}

 

Задача 3. Алгоритм накопления произведения

Дана последовательность:

cos 0.1, cos 0.2, cos 0.3, ..., cos 10.

Вычислить значение: Р 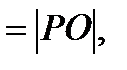где РО - произведение отри­цательных членов последовательности.

 

Решение

Общий член последовательности имеет вид:

y = cos x, где 0.1 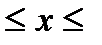10; Δх = 0.1.

Для реализации алгоритма накопления произведения выделяется ячейка памяти РО, в которой осуществляется последова­тельное перемножение отрицательных членов последовательно­сти с помощью оператора присваивания РО=РО*у; . В началь­ный момент в ячейку должна быть занесена единица оператором РО=1;.

#include "stdafx.h"

#include<math.h>

int main()

{

float х, у, Р, РО;

РО = 1;// установка нач. значения произведения

for (x=0.1; x<=10; x=x+0.1)//запуск цикла

{

у = cos(x);

if ( y<0) РО = РО*у;

}

Р = fabs(PO);

printf("P=%6.2f",P); //вывод на экран значения P

return 0;

}

 

Задача 4. Алгоритм поиска минимального члена после­довательности

Дана последовательность:

a_k=e^ktg(2k + l); к= .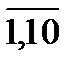

Найти минимальный член последовательности.

Решение

Для реализации алгоритма выделяется ячейка памяти min, в которую сначала заносится первый член последовательности. Затем, начиная со второго, производится сравнение очередного вычисленного члена последовательности с содержимым ячейки min. Если текущий член последовательности меньше содержимого ячейки min, то oн переписывается в эту ячейку. В противном случае содержимое ячейки min сохраняет прежнее значение. При завершении сравнения всех членов последовательности в ячейке min остается минимальное значение.

Замечание 1. Алгоритм поиска максимального члена последовательности отличается от поиска минимального члена лишь тем, что в ячейке (ей можно дать, например, имя max) запоминается больший из сравниваемых членов последовательности.

Замечание 2. В начальный момент в ячейку min можно занести не первый член последовательности, а достаточно большое число, которое превышало бы область определения сравниваемых чисел (например, min=+1E6;). Тогда при сравнении с содержимым ячейки min первый член последовательности обязательно окажется меньше и перепишется в ячейку min. При поиске максимального члена последовательности в ячейку max в начальный момент заносится, наоборот, достаточно малое число, которое должно быть меньше всех сравниваемых членов последовательности (например, mах= -1Е6;). В этом случае первый из сравниваемых членов последовательности окажется больше содержимого ячейки max и запишется в эту ячейку.

Программа поиска min:

#include "stdafx.h"

#include<math.h>

int main()

{

float a, min;

int k;

min = +1E6; // нач. значение переменной min

for( k=l; k<=10;k++)

{

a = exp(1.0*k)*tan(2*k + 1.0);

if (a<min) min = a; // условие для поиска min

}

printf("min=%6.2f", min);

return 0;

}

Задача 5. Табулирование функции (или кратные циклы)

Тело цикла может содержать любой оператор, в том числе и другой оператор цикла. Структура цикла, содержащая вло­женный цикл, называется кратным циклом. Число вложений может быть произвольным. Если цикл содержит один вложенный цикл, то он называется двойным, если содержит два вложенных цикла, то является тройным и т.д. Цикл, ко­торый содержит вложенный цикл, называется внешним. Вло­женный цикл называется внутренним.

Переменная внутреннего цикла всегда меняется быстрее, чем внешнего. Это означает, что для каждого значения внешней пе­ременной цикла меняются все значения внутренней переменной.

Внешний и внутренний циклы могут использовать любой вид операторов цикла (while, do-while, for).

Пример.Алгоритм табулирования функции с двумя пе­ременными

Вычислить значение функции:

z(x, у) = sin x + cos y

при всех х, изменяющихся на интервале [-1, 1] с шагом Δх = 0.2, и у, изменяющихся на интервале [0, 1] с шагом Δу = 0.1.

Данный алгоритм реализуется с использованием двойного цикла, в котором х примем за внешнюю переменную цикла, у - за внутреннюю переменную цикла.

#include "stdafx.h"

#include<math.h>

int main()

{

float х, у, z; // описание переменных

printf("x y z(x,y)\n"); // вывод заголовка

x= -1; // начальное значение параметра внешнего цикла

while (х<=1) // запуск внешнего цикла, если х≤ 1

{

for( y=0; y<=1; y=y+0.1) //запуск внутреннего цикла

{

z=sin(x) + cos(y); // вычисление функции

printf("%6.1f %6.1f z=%6.1f",x, y, z); // вывод

}

x=x + 0.2; // изменение параметра х на шаг

}

return 0;

}

 

В результате выполнения программы вид таблицы на экране будет следующим:

x	y	z(x,y)
-1.0	0.0	z=…
-1.0	0.1	z=…
…	…	…
-1.0	1.0	z=…
-0.8	0.0	z=…
-0.8	1.0	z=…

Задача 6. Вычисление сумм последовательностей

Последовательности с заданным числом элементов

Пример 1.Найти сумму первых 20 элементов последовательности

S=1/2 – 2/4 + 3/8 – 4/16+…

Чтобы решить эту задачу, надо определить закономерность в изменении элементов. В данном случае можно заметить:

· Каждый элемент представляет собой дробь.

· Числитель дроби при переходе к следующему элементу возрастает на единицу.

· Знаменатель дроби с каждым шагов увеличивается в 2 раза.

· Знаки перед дробями чередуются (плюс, минус и т.д.).

Любой элемент последовательности можно представить в виде

S=z*c/d

У переменной z меняется знак (эту операцию можно записать в виде z=-z), значение переменной c увеличивается на единицу (c++), а переменная d умножается на 2 (d=d*2).

Алгоритм решения задачи можно записать в виде следующих шагов:

· Записать в переменную S значение 0. В этой ячейке будет накапливаться сумма;

· Записать в переменные z, c и d начальные значения (для первого элемента): z=1, c=1,d=2;

· Сделать 20 раз следующие две операции:

v добавить к сумме значение очередного элемента;

v изменить значения переменных z, c и d для вычисления следующего элемента.

 

 

#include "stdafx.h"

int main()

Начальные значения

{

float S, z, c, d;

int i;

S = 0; z = 1; c = 1; d = 2;

добавить элемент к сумме

for ( i = 1; i <= 20; i ++ )

{

S = S + z*c/d;

изменить переменные

z = - z;

c++;

d = d * 2;

}

printf("Сумма S = %f", S);

return 0;

}

Суммы с ограничивающим условием

Рассмотрим более сложную задачу, когда количество элементов заранее неизвестно.

Пример 2.Найти сумму всех элементов последовательности

S=1/2 – 2/4 + 3/8 – 4/16+…

которые по модулю меньше, чем 0.001.

Эта задача имеет решение только тогда, когда элементы последовательности убывают по модулю и стремятся к нулю. Поскольку мы не знаем, сколько элементов войдет в сумму, надо использовать цикл while (или do - while). Один из вариантов решения показан ниже.

 

#include<math.h>

#include "stdafx.h"

начальные значения

int main()

{

Запустить цикл, если а ≥0.001

float S, z, c, d, a;

S = 0; z = 1; c = 1; d = 2;

a = 1;

while ( a >= 0.001 )

добавить элемент к сумме

{

a =fabs( c / d);

изменить переменные

S = S + z*a;

z = - z;

c ++;

d = d * 2;

}

printf("Сумма S = %f", S);

return 0;

}

 

Цикл закончится тогда, когда переменная a (она обозначает модуль очередного элемента последовательности) станет меньше 0.001. Чтобы программа вошла в цикл на первом шаге, в эту переменную надо записать любое значение, большее, чем 0.001.

Очевидно, что если переменная a не будет уменьшаться, то условие в заголовке цикла всегда будет истинно и программа «зациклится».