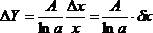Оценка погрешностей косвенных измерений

Чтобы понять основной принцип оценки погрешностей косвенных измерений, следует проанализировать источник этих погрешностей.

Пусть физическая величина Y есть функция непосредственно измеряемой величины х, Y = f(x).

Величина х имеет погрешность Dх. Именно эта погрешность Dх – неточность в определении аргумента x является источником погрешности физической величины Y, являющейся функцией f(x).

Приращение Dх аргумента х определяет собой приращение функции .

Погрешность аргумента Dх косвенно определяемой физической величины Y определяет собой погрешность , где Dх – погрешность физической величины, найденной в прямых измерениях.

Если физическая величина является функцией нескольких непосредственно измеряемых величин , то, проводя аналогичные рассуждения для каждого аргумента xi, получим:

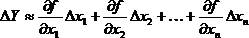
Очевидно, что погрешность, рассчитанная по этой формуле, является максимальной и соответствует ситуации, когда все аргументы изучаемой функции имеют одновременно максимальное отклонение от своих средних значений. На практике такие ситуации маловероятны и реализуются крайне редко, поэтому следует рассчитывать погрешность результата косвенных измерений .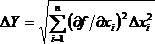

В реальных измерениях относительная точность различных величин хi может сильно отличаться. При этом, если для одной из величин xm выполняется неравенство 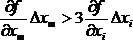, где i = 1,…, m – 1, m + 1, …, n, то можно считать, что погрешность косвенно определенной величины D_Y определяется погрешностью D_xm: .

Итак, при вычислении погрешности косвенно определяемой физической величины 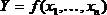надо прежде всего выявить наименее точно определенную в прямых измерениях величину 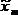и, если 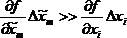, считать , пренебрегая погрешностями остальных х_ii¹m.

Рассмотрим наиболее распространенные случаи взаимосвязи физических величин.

1. Степенная зависимость 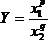, где p, q - любые числа.

В данном случае проще сначала вычислить относительную погрешность .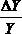

2. Прологарифмируем 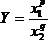, получим .

3. Продифференцируем это равенство: .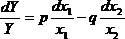

4. Перейдем от бесконечно малых приращений – дифференциалов к конечным приращениям Dх1, Dх2: .

5. Учтем, что Dх1 и Dх2 – величины алгебраические и могут быть как положительными, так и отрицательными. Нашей же целью является выявление максимально возможной погрешности, поэтому нас будет интересовать наихудшая ситуация, которая реализуется при D_х1 > 0, а D_х2 < 0. Вследствие этого при вычислении погрешности δY все минусы заменяются на плюсы, и мы имеем:

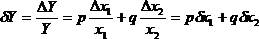6. Это выражение дает завышенную погрешность. Более точная формула полученная из теории ошибок [3, 4, 5] имеет вид: .

7. Следует заметить, что чем больше по модулю показатель степени, тем большую погрешность вносит данная переменная в погрешность результата. В данном случае следует также сравнить между собой и найти среди них максимальное значение 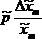. Если для всех остальных i¹m, то 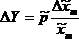, и абсолютная погрешность .

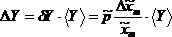8. Логарифмическая зависимость .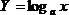

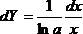, переходя от дифференциалов к конечным приращениям, имеем: .

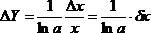В этом случае абсолютная погрешность D_Y пропорциональна относительной погрешности непосредственно измеряемой величины x. Если Dx= const, то с ростом х D_Y будет уменьшаться (вот почему графики логарифмических зависимостей 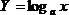, как правило отличаются неравновеликими погрешностями DY).

Итак, для логарифмических функций вида Y = A logax проще сразу вычислять абсолютную погрешность, которая пропорциональна относительной погрешности переменной x :