Системы счисления.

Система счисления (СС)– совокупность приёмов и правил для изображения чисел с помощью символов, имеющих определённые количественные значения. В любой системе счисления выделяют некоторые числа, которые называют узловыми; другие числа – алгоритмические, получаются в результате выполнения каких-либо операций над узловыми. Например, в римской системе счисления узловыми являются числа I(1), V(5), X(10), L(50), C(100), D(500), M(1000). Алгоритмическими числами являются, например, числа II, III, IV, VI, VII, VIII, IX, LX(60) , CXXI(121). Если в римской СС меньшее узловое число стоит слева от другого узлового числа, то оно вычитается, а если справа – то прибавляется к соседнему. Например, XII = 10+2; XIX= X + IX = 10+9; XL = 50 - 10 = 40 и т.д. Существуют алфавитные СС, в которых для записи чисел используются буквы. Например, в церковно-славянском языке для записи чисел используются буквы: А(1), В(2), Г(3), Д(4), Е(5), S(6), I (10), К(20). Тогда, например, IД = 14, КЕ = 25.

Системы счисления делятся на позиционные и непозиционные. В непозиционных системах счисления количественное значение каждой цифры не зависит от её позиции в записи числа. Непозиционные СС возникли раньше позиционных систем. Римская СС является непозиционной: например, в записи чисел XV и VII значение символа V (5) не зависит от его позиции в записи чисел.

Если значение числового символа зависит от его расположения в записи числа, то такая СС называется позиционной. Её изобретение, приписываемое шумерам и вавилонянам, имело неоценимые последствия в истории человеческой цивилизации. Дальнейшим развитием позиционной системы занимались индусы. Позиционные системы более удобны для вычислений, чем непозиционные. В настоящее время используются в основном позиционные системы счисления.

К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась благодаря итальянским купцам, которые в свою очередь заимствовали её у мусульман. «Позиционность» десятичной системы поясним на примере. В записи числа 525.351 цифра 5 встречается три раза, и её значение зависит от позиции в записи. Первая позиция слева - это количество сотен (500), третья слева - это количество единиц (5), а вторая после десятичной точки - это количество сотых долей (5/100) или (5*10^-2). Любая позиционная СС характеризуется своим основанием – количеством знаков, используемых для изображения чисел.

Для нас привычной является десятичная система счисления с основанием 10. В ней для записи чисел используются десять различных цифр: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Основание позиционной СС не обязательно равно 10, а может быть любым натуральным числом большим 1. Например, если СС имеет основание 3, то используются три цифры {0,1, 2}, а числа могут записываться в виде 211₃, 102.21₃ – нижний индекс указывает на основание СС, в которой сделана запись числа. Далее будем обозначать 2-ую, 8-ую и 16-ую СС как Bin, Oct и Hex соответственно. Десятичную систему счисления обозначим как Dec.

Приведём общее правило для изображения чисел в позиционной системе счисления. Пусть задано основание системы счисления – натуральное число B >1. Задан алфавит (цифры) системы счисления, содержащий В символов. Пусть M ={A1, A2, …, AB} - алфавит системы счисления; а R_k – знаки алфавита M, k = -n, -n +1, …. 0, 1, 2, … m, где m, n - неотрицательные целые числа. Здесь индекс k указывает на позицию в записи числа, в которой стоит знак R_k .

Позиционной записью числа Х в системе счисления с основанием В называется его представление в виде:

Х = R_m R_m-1 R_m-2… R₁ R₀ · R _-1R_-2 … R_-_n(9.1)

В формуле (9.1) символ «·» - разделитель целой и дробной части числа X; обычно это точка « . » или запятая « , ». Номер позиции цифры в записи числа определяется относительно разделителя: влево или вправо. Отсчёт влево идёт с нуля. В формуле (9.1) R₄означает, что эта цифра находится на 5-ой позиции, если считать от разделителя влево (5, а не 4, так как отсчёт идет с нуля); R_-3 означает, что эта цифра стоит на третьей позиции, если считать от разделителя вправо.

Запись (9.1) означает, что число X равно:

X= R_m*B^m + R_m-1*B^m-1 + R_m-2*B^m-2 +… R₁*B¹ +R₀* B⁰+R _–1*B^-1 +R_-2*B^-2 +… R _–n * B^-n,

где B⁰=1; B^m = B*B*…..B, т.е. В умножаем на себя m - раз; B^-n = 1/Bⁿ.

Более компактная запись формулы (9.1) :

. (9.2)

Например, для «обычной» десятичной системы счисления с основанием В=10 и М={0,1,2,3,4,5,6,7,8,9}, запись (9.1) для X= 3269.721 означает, что Х=3*10³ + 2*10² + 6*10¹ + 9*10⁰ + 7*10^-1 + 2*10^-2 + 1*10^-3.

Основание позиционной СС – это количество единиц младшего разряда, переходящее в единицу старшего соседнего разряда. Используя это правило, выпишем первые 16 натуральных чисел в двоичной системе счисления (Bin) , используя «таблицу сложения» 1+0 = 1; 1+1 = 10:

0+1 = 1	100+1 =101	1000+1=1001	1100+1=1101
1+1 = 10	101 +1 =110	1001+1=1010	1101+1=1110
10+1 = 11	110 +1 = 111	1010+1=1011	1110+1=1111
11+1 = 100	111+1 =1000	1011+1=1100	1111+1= 10000

В 8-ой СС (Oct) используются первые восемь цифр десятичной системы {0, 1, 2, 3, 4, 5, 6, 7}. Выполняются соотношения

7+1=10		13+1=14
10+1=11		14+1=15
11+1=12		15+1=16
12+1=13		16+1=17
		17+1=20

В Hex используются десять цифр 0, 1, … 9, а недостающие цифры изображают с помощью букв A, B, C, D, E, F: A= 9+1, B=A+1, C=B+1, D=C+1, E=D+1, F=E+1, F+1=10₁₆.

В сводной таблице 1 представлены натуральные числа от 1 до 16 в 2- ой , 8-ой и 16-ой системах счисления. Обратите внимание на то, что в таблице для записи двоичного представления чисел всегда используются 4 бита, хотя для записи чисел от 1 до 7 достаточно 1, 2 или 3 бит. Такое 4-х битовое представление нам понадобится в дальнейшем при переводе чисел из Bin в Hex, и наоборот.

Таблица 1.

Dec	Bin	Oct	Hex










			A
			B
			C
			D
			E
			F

Пример 1. Приведём пример позиционной записи (1) для чисел в Bin. Рассмотрим двоичное число:

11100101.101

Это дробное число; для его перевода в Dec надо использовать формулу (9.2):

2⁷ + 2⁶ + 2⁵+ 2² + 2⁰ + 1/2 + 1/2³ =

128 + 64 + 32 + 4 + 1 + 0.5 +0.125 = 229. 625.

Таким образом, формула (2) даёт способ перевода чисел из Bin в Dec.

Пример 2. Перевести из Bin в Dec число 101.011. Запишем данное число в виде (9.2):

101.011 = 1*2²+ 0*2¹ + 1*2⁰ +0*2^-1 + 1*2^-2 + 1*2^-3=4+0+1+1/2 +1/4=4.75

Алгоритм перевод чисел из Dec в Bin поясним на примерах.

Пример 2. Перевести из Dec в Bin число 42.73

Отдельно переведем целую и дробную части числа.

a) Для перевода целой части (= 42) проводим ряд последовательных делений десятичного числа 42 на 2. При каждом таком делении находим частное (r) и остаток (q). На каждом шаге полученное частное вновь делим на 2 и т.д. Процесс останавливается, когда при очередном делении частное будет равно 0.

42 : 2 = 21 (0) r = 21, q = 0

21 : 2 = 10 (1) r = 10, q = 1

10 : 2 = 5 (0) r = 5, q = 0

5 : 2 = 2 (1) r = 2, q = 1

2 : 2 = 1 (0) r = 1, q = 0

1 : 2 = 0 (1) r = 0, q = 1 (Stop)

Полученные остатки q выписываем, начиная с самого последнего и до первого. Это и будет двоичный код числа 42: 42₁₀ =101010₂ .

b) Для перевода дробной части 0.73 заданного десятичного числа в Bin проводим ряд последовательных умножений на 2. В полученном произведении на каждом шаге отделяем целую часть (r) от дробной (q). Дробную часть вновь умножаем на 2 и т.д. Процесс заканчивается, если на очередном шаге дробная часть будет равна нулю. Здесь возможны случаи, при которых очередная дробная часть q уже встречалась на предыдущих шагах процесса, то есть мы получим периодическую двоичную дробь. Если такой момент не наступает, мы имеем дело с бесконечной двоичной дробью. Выписываем полученные целые части r в порядке их появления от первой до последней - это и будет искомая двоичная дробь.

0. 73 * 2 = 1. (46 ) r =1, q= 0.46

0. 46 * 2 = 0. (92 ) r =0, q= 0.92

0. 92 * 2 = 1. (84 ) r =1, q= 0.84

0. 84 * 2 = 1. (68 ) r =1, q= 0.68

0. 68 * 2 = 1. (36 ) r =1, q= 0.36

и т.д. Мы прервали перевод дроби 0.73 и получили её приближенное представление в виде дроби системы Bin: 0. 73 » 0.10111…

Окончательно получаем: 42.73 » 101010.10111…

Пример 2.

Записать в Bin десятичное число 0.15 (в виде двоичной дроби).

0.15 * 2 = 0. (3) r = 0, q = 0.3

0.3 * 2 = 0. (6) r = 0, q = 0.6

0.6 * 2 = 1. (2) r = 1, q = 0.2

0.2 * 2 = 0. (4) r = 0, q = 0.4

0.4 * 2 = 0. (8) r = 0, q = 0.8

0.8 * 2 = 1. (6) r = 1, q = 0.6

0.6 * 2 = 1. (2) r = 1, q = 0.2 – повторение: см. строку 3.

Получили представление числа 0.15 в виде двоичной периодической дроби:

0.15 = 0.00100110011001…= 0.00(1001).

Пример 3. Если знаменатель дроби является степенью двойки, то можно использовать следующий приём для перевода дроби из Dec в Bin. Покажем, как можно записать в двоичной системе дроби 3/4, 5/8, 13/16:

3 = 11₂, 4 = 100₂ ® 3/4 = (11/100)₂ = 0.11;

5 = 101₂, 8 =1000₂ ® 5/8 = (101/1000)₂ = 0.101;

13 = 1101₂, 16 = 10000₂ ® 13/16 = (1101/10000)₂ = 0.1101

Техника перевода чисел из Hex в Dec такая же, как и в случае перевода из Bin в Dec.

Пример 4. Задано дробное число 3FA.B5 в Hex. Записать это число в Dec. Используем формулу (9.2):

3FA.B5 = 3*16² +F*16¹ +A*16⁰ + B*16^-1 + 5*16^-2

= 3*256 + 15*16 +10 + 11/16 +5/256

=768+240+10+(11*16+5)/256=1018 +181/256 »1018.70703125…

Пример 5. Перевести десятичное число 332 в Hex.

Как и при переводе из Dec в Bin делим заданное целое на 16 и при каждом таком делении находим частное (r) и остаток (q). Полученное частное вновь делим на 2 и т.д. Если остаток 10£ q £ 15, то заменяем его на соответствующие буквенные изображения цифр Hex, см таблицу 1. Затем выписываем остатки по порядку «снизу – вверх»:

332 : 16 = 20 (12), 12 это С₁₆

20 : 16 = 1 (4)

1 : 16 = 0 (1)(Stop)

332₁₀ = 14С₁₆ .

Дробные числа из Dec переводятся в Hex, как и в случае перевода из Dec в Bin. Например, переведём дробь 0.13 в Hex:

0.13*16 = (2). 08

0.08*16 = (1). 28

0.28*16 = (4). 48

0.48*16 = (7). 68

0.68*16 = (A). 88, A₁₆=10

0.88*16 = (E). 08, E = 14, остаток 08 уже встречался, см. 2 строку.

Т.е. при переводе числа 0.13 в Hex мы получили периодическую дробь: 0.13 = 0.2147AE147AE… = 0.2(147AE)₁₆ .

При переводе дробей, знаменатель которых является степенью 16, можно использовать более простой способ. Например, переведём дробь 11/16 в Hex: 11=B₁₆, 16=10₁₆ ; тогда (11/16) = (B/10)₁₆ = 0.B ; переведём дробь 167/256 в Hex: 167 = A7₁₆; 256 = 100₁₆ ; значит (167/256) = (A7/100) = 0.A7.

Для перевода чисел из Bin в Hex применяется следующий приём: двоичную запись числа надо разбить на группы цифр по 4 (на тетрады), начиная от разделителя влево и вправо (если число дробное). Самую левую и самую правую тетрады дополняем, если надо, нулями. Каждую двоичную тетраду нужно заменить на соответствующую цифру в Hex, используя таблицу 1. Пример:

111011001.110111 = 1 1101 1001 . 1101 11 =

0001 1101 1001 . 1101 1100 = 1D9. DC .

Перевод из Hex в Bin осуществляется ещё проще: каждую цифру числа, записанного в Hex, нужно заменить на соответствующую тетраду из таблицы 1. Например, A7C.2F = 1010 0111 1100. 0010 1111;

Значение систем Bin и Hex для информатики определяется тем, что все данные и программы представлены в компьютере в двоичной системе. Для большей «читабельности» двоичных кодов их выводят на экран в Hex; адреса памяти записываются в Hex; дампы памяти представляют в Hex.

Для записи чисел в компьютере используются два основных способа: с фиксированной запятой и с плавающей точкой.

Систему представления чисел с фиксированной запятой обозначают как P(b, t, f), где b – основание системы счисления, t – количество разрядов для записи числа, f - количество разрядов для записи дробной части.

Рассмотрим пример системы с фиксированной запятой Р(10, 4, 1); здесь b=10, t=4, f=1. Т.е. это Dec, общее количество разрядов для записи числа равно 4, под дробную часть отводится 1 знак. Минимальное число, которое можно записать в этой системе, равно -999.9, максимальное число равно +999.9, всего положительных чисел с нулём 10000, всего отрицательных чисел 9 999. Любое число из [ -1000; 1000] представимо в системе Р(10, 4, 1) с ошибкой £ 0.05

Пример. Пусть задано число x=865.54. Его представление в P(10, 4, 1) обозначим как p(x) = 865.5. Ошибка равна | x - p(x)| = 0.04. Относительная ошибка представления этого числа Е = | x - p(x)| /x = 0.04 / 865.54 = 0.000046213, что составляет » 0.004%.

Если х = 0.86554, то р(х) = 0.9 (произвели округление при записи числа в системе P(10, 4, 1) ), относительная ошибка Е = 0.03446/0.86554 = 0.039813…, что составляет »3.98%.

Вывод: система P(b, t, f) образует равномерную сетку для представления вещественных чисел, но относительная ошибка при записи вещественных чисел в этой системе не является равномерной.

Система P(b, t, f) используется в современных ЭВМ только для записи целых чисел в двоичной системе(со знаком и без знака), то есть при b = 2, f = 0. Для записи целых чисел в современных компьютерах может отводиться, например, 8, 16 или 32 бита, т.е. t=8, 16, 32. Выделенные для записи чисел биты нумеруются справа налево, начиная с нуля. Если целое число со знаком, то старший бит хранит знак числа: 0 соответствует знаку плюс, 1 соответствует знаку минус.

Пример. Целые числа со знаком в системе Р(2, 8, 0). Для их записи отводится 8 бит. Старший (седьмой) бит содержит знак числа: 0 или 1. Вот как будет записано число +75 = 2⁶+2³ +2¹+2⁰ в 8-битовом коде:

0100 1011.

Степени двойки в записи числа +75 указывают на то, что бит с соответствующим номером содержит 1.

7 бит (знак)	6 бит	5 бит	4 бит	3 бит	2 бит	1 бит	0 бит

Для записи отрицательных целых чисел используется дополнительный код. Правило для записи отрицательного числа (-N) в дополнительном коде:

1) записать двоичный код соответствующего положительного целого N и дополнить его слева до нужного числа битов нулями (до 8, или до 16, или до 32 битов).

2) инвертировать полученный код (операция инверсии двоичного кода заключается в замене всех 0 на 1 и всех 1 на 0);

3) прибавить к младшему разряду инвертированного кода 1. Полученный код и будет дополнительным кодом отрицательного числа (-N).

Пример 1. Записать дополнительный 8 битовый код числа -95. Решение: запишем 95 в двоичном коде: 95 = 64+16+8 +4+2+1 = 101 1111. Дополним этот код слева нулём (чтобы получилось 8 бит): 0101 1111. Инвертируем полученный код: 1010 0000. Прибавим 1 к младшему разряду данного кода: 1010 0001. Это и будет дополнительный двоичный код отрицательного числа -95. Для проверки сложим полученные коды:

+ 95 : 0 1 0 1 1 1 1 1

-95 : 1 0 1 0 0 0 0 1

сумма : (1) 0 0 0 0 0 0 0 0

Сумма единиц в 8-ом бите перешла в 9-ый бит, который отсутствует в записи числа – он теряется (говорят, что произошел перенос из знакового бита), и сумма становится равной 0.

Максимальное положительное 8-ми битовое число 0111 1111 = +127. Восьми битовое число 1000 0001 = -127. Минимальное отрицательное 8-ми битовое равно 1000 0000 = -128. Т.е. диапазон однобайтовых целых чисел со знаком от -128 до +127. Всего с помощью 8-ми бит можно представить 256 чисел, т.е. 2⁸.

Для перевода отрицательных чисел из дополнительного кода поступаем также: инвертируем код отрицательного числа, прибавляем 1 к младшему разряду и получаем двоичный код соответствующего положительного числа.

Пример. Какое целое число со знаком записано в 8-ми битовом коде 1010 0011? Решение: Старший бит равен 1, значит это отрицательное число. Инвертируем данный код: 0101 1100; Прибавляем 1 к младшему разряду: 0101 1101. Переводим это число в Dec: 2⁶+2⁴+2³+2²+2⁰ = 64+16+8+4+1 = 93. Т.е. заданный дополнительный код соответствует числу -93.

В языке программирования Turbo Pascal используются, например, такие целые типы данных:

Тип данных	Размер памяти	Количество чисел	Диапазон
Byte	1 байт	2⁸ = 256	0 ..255
ShortInt	1 байт	2⁸= 256	-128 .. 127
Word	2 байта	2¹⁶ = 65 536	0 .. 65 535
Integer	2 байта	2¹⁶ = 65 536	-32 768 .. 32 767

Пояснения к таблице. Типы ShortInt и Integer используются для записи целых со знаком, т.е. старший бит хранит знак числа; типы Byte и Word используются для записи целых без знака (неотрицательных); 1 байт = 8 бит; используя n бит можно записать 2ⁿ различных чисел (доказывается по индукции). Покажем, что максимальное число, которое можно представить, используя n бит равно (2ⁿ– 1). Действительно, если имеется n бит для записи числа, то максимальное число получится в случае, когда все разряды (биты) равны 1:

Если к этому числу прибавить 1, получим число:

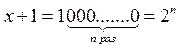т.е. x = 2ⁿ -1.

Для правильной интерпретации содержимого памяти нужно знать, какой тип данных в ней храниться, т.к. по «внешнему виду» отличить один тип от другого нельзя. Пусть, например, 1 байт памяти содержит следующие данные: 1001 1101. Если это число типа Byte, то оно равно 2⁷+2⁴+2³+2²+2⁰= 128+16+8+4+1=157. Если это целое число со знаком типа ShortInt, то для его определения надо инвертировать код: 0110 0010, затем прибавить 1: получим 0110 0011, т.е. 2⁶+2⁵+2¹+2⁰= 64+32+2+1 = 99, значит, данный байт содержит число - 99.

Система представления чисел с плавающей точкой F(b, t, L, U). Такая система используется для записи вещественных чисел в современных ЭВМ. Здесь b – основание системы (для ЭВМ b равно 2), t - количество разрядов мантиссы, L , U – пределы изменений значений показателей порядка чисел в этой системе. Пример числа, записанного в виде числа с плавающей точкой: 0.31562781*10⁵; здесь 0.31562781 – мантисса числа, 5 – его порядок. Это число в «обычной», позиционной записи выглядит как 31562.781. Такой способ представления чисел позволяет компактно записывать числа из широкого диапазона значений, например:

0.4671*10^-15, или 0.8965*10¹².

Числа системы F(b, t, L, U) имеют вид: x = ± M*b^k, где M – мантисса числа x, b – основание системы счисления, k – порядок числа x. Развёрнутая запись числа x:

(9.3)

или, более компактно:

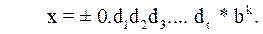(9.4)

Здесь d₁, d₂, d₃, …. d_t- цифры системы счисления; они составляют мантиссу числа; t – разрядность мантиссы (количество знаков в мантиссе).

Должны выполняться следующие условия:

1) 1 £ d₁ < b (первая цифра мантиссы не должна равняться нулю);

2) 0 £ di < b , i =2,3,…t ;

3) L £ k £ U.

Если мантисса удовлетворяет первому условию, то говорят, что число представлено в нормализованном виде (с нормализованной мантиссой).

Запись нуля в системе F(b, t, L, U): 0.000…0* b^L .

Утверждение 1. Система F(b, t, L, U) содержит

2*(b-1)_*b^t^-1 _*(U-L+1) +1 различных чисел.

Утверждение 2. Числа системы F(b, t, L, U) образуют неравномерную сетку, но относительная плотность этой сетки равномерна (всюду одинакова).

Пример 1. Система F(10, 4, -2, 3). Здесь b=10, t=4, L= -2, U=3. Число x=865.54 в этой системе записывается в виде F(x) = 0.8655*10³ , а число y=0.86554 имеет вид F(y) = 0.8655*10⁰. В обоих случаях относительная ошибка » 0.005%. Действительно,

| F(x) – x| /x =0.04/865.54 =4/86554;

| F(y) –y | /y = 0.00004/0.86554 = 4/86554.

В отличие от системы с фиксированной точкой, здесь относительная ошибка представления чисел одинакова для всех чисел из заданного диапазона.

Пример 2. Системы F(2, 3, -1, 2). Здесь b=2 (двоичная система), t=3, L= -1, U=2. Выпишем все положительные числа этой системы. Сначала заполним столбец числами порядка 2⁰; числа из соседних столбцов получаются умножением (делением) на 2.

числа порядка 2^-1	числа порядка 2⁰	числа порядка 2¹	числа порядка 2²
0.100 ~ 4/16 = ¼	0.100 ~ 4/8 =1/2	0.100 ~ 4/4 =1	0.100 ~ 4/2 = 2
0.101 ~ 5/16	0.101 ~ 5/8	0.101 ~ 5/4	0.101 ~ 5/2 = 2.5
0.110 ~ 6/16	0.110 ~ 6/8	0.110 ~ 6/4	0.110 ~ 6/2 = 3
0.111 ~ 7/16	0.111 ~ 7/8	0.111 ~ 7/4	0.111 ~ 7/2 = 3.5

Систему счисления с плавающей точкой F(b, t, L, U)можно описать с помощью чисел e, s, l:

1) e (машинное e) – это минимальное положительное число, которое будучи сложенным с 1, даёт результат ¹ 1. Вычислим его. Т.к. ближайшее справа к 1 число это 0.1000 ..1*b, значит e равно разности между этим числом и 1, т.е. e = 0.10…1*b – 0.1*b = b^1-t , для приведённого выше примера e = ¼.

2) s - минимальное положительное число системыF(b, t, L, U).Оно равно расстоянию между нулём и ближайшим к нему числом системы F(b, t, L, U). Это число представимо в виде: (минимальная мантисса) * b^L : s = 0.1*b^L = b^L^-1,для приведённого выше примера s = ¼ ;

3) l – максимальное число системы F(b, t, L, U). Это число представимо в виде: l = (максимальная мантисса) * b^U, т.е.l = 0.11…1*b^U = b^U*(1 – 0.00…1) = b^U*(1-b^-^t).Для приведённого выше примера l= 3.5.

Система чисел с плавающей точкой используется для представления дробных чисел в памяти ЭВМ. В самом общем виде структура представления вещественных чисел в ЭВМ имеет следующий вид:

Знак мантиссы

Знак порядка

Порядок числа

Мантисса

Для хранения знака мантиссы и знака порядка числа отводится по 1 биту; количество бит для хранения порядка и мантиссы зависит от выбранного типа представления данных. Например, если для хранения дробного числа отведено 32 бита, то их назначение может быть распределено следующим образом (в первой строке стоят номера битов, старший бит под номером 31 - знак числа, мантисса хранится в битах с номерами от 0 до 22, порядок числа в битах с номерами от 23 до 30):

			…..				…..
Знак числа	Порядок числа	Мантисса

Так как в нормализованной мантиссе двоичного числа в первой позиции всегда стоит единица, то хранят мантиссу, начиная со второго знака. Например, число 0.1101*2⁵ хранится как 1.101*2⁴ , при этом единица целой части числа не хранится. Корректировка происходит при преобразовании числа или в ходе вычислений. При этом порядок дробного двоичного числа при хранении занимает 1 байт и изменяется в диапазоне от -127 до +128, а не от -128 до +127, как было бы в случае нормализованного представления чисел. Например, если надо записать число 0.11*2^-127 , то представляем его как 1.1*2^-128 ; число 0.11011*2⁺¹²⁸ =1.1011*2⁺¹²⁷ . Далее, чтобы порядок числа всегда был положительным к нему прибавляют 127, т.е. если порядок числа -10, то хранится +117. Порядок 100 хранится как 227. Такой способ записи порядка называют смещённым.

Примеры. 1. Как будет представлено в памяти компьютера число - 0.0625, если для его размещения выделено 32 бита памяти?

Решение: 0.0625 = 1/16 = 0.0001₂, т.е. -0.0625 = -0.1*2^-3 = -1.0*2^-4 ;

смещенный порядок равен (-4+127) = 123, или в Bin 123 = 1111011₂ ; мантисса = 0 ( все 23 бита). Старший бит равен 1, т.к. число отрицательное. Окончательно получаем:

1 0111 1011 000 0000 0000 0000 0000 0000.

2. Запишите число 25 как число с плавающей запятой, используя 32 бита. Решение: 25 = 11001₂ = 1.1001*2⁴ . Смещённый порядок равен 4+127 = 131 или 10000011_{2 .} Мантисса = 1001, окончательно получаем:

0 1000 0011 100 1000 0000 0000 0000 0000.

В языке TurboPascal существуют следующие типы данных для хранения вещественных чисел:

Тип данных	Размер памяти	Разрядн. мантиссы (бит)	Порядок величин
Real	6 байт		10³⁸
Single	4 байт		10³⁸
Double	8 байт		10³⁰⁸
Extended	10 байт		10⁴⁹³²

Очевидно, что множество вещественных чисел R значительно отличается от множества рациональных чисел, с которыми мы имеем дело в ЭВМ. Для чисел, представленных в ЭВМ можно указать наибольшее по модулю число А, такое что все остальные числа будут меньше, чем А. Кроме того, не выполняется свойство «всюду плотности» множества вещественных чисел, суть которого состоит в том, что для любых x, y (x < y) из множества R, можно указать значение z, такое, что x < z < y. Должна быть разработана теория «машинных» действительных чисел. Неточный перевод действительных чисел в двоичную систему и конечность разрядов, выделяемых для хранения чисел, служат источниками систематических ошибок при реализации многочисленных вычислительных методов на ЭВМ.