Система и совокупность неравенств с одной переменной

Поскольку неравенство, содержащее подмножество , есть предикат, то можно говорить о конъюнкции и дизъюнкции неравенств.

Определение. Пусть – неравенство, определенное на множестве ; – неравенство, определенное на множестве и т.д. – неравенство, определенное на множестве .

Конъюнкцию предикатов ; ; …; называют системой данных неравенств и записывают:

Аналогично определяют систему неравенств со знаками , , .

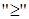Область определения системы неравенств с одной переменной есть множество .

Значения переменной, при которой каждое неравенство системы обращается в верное числовое неравенство, называют решением системы неравенств.

Решить систему неравенств - следовательно, найти все решения этой системы или установить, что их нет.

Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему.

Две системы неравенств называют равносильными, если всякое решение одной из них является решением другой, и наоборот. Если обе системы неравенств не имеют решений, то их тоже считают равносильными.

Пример. Решим систему неравенств:

Решение. Данная система неравенств равносильна системе:

Таким образом, множество решений системы есть интервал , который является пересечением интервалов и .

Пример. Решим систему неравенств

Решение. Решим первое неравенство: , , . Неравенство выполняется при .

Решим второе неравенство: , , . Неравенство выполняется при .

Решим третье неравенство: , , . Неравенство выполняется при .

Все три данных неравенства верны при .

Ответ. .

Пример. Решим неравенство: .

Решение. Имеем или . Дробь отрицательна только в тех случаях, когда ее числитель и знаменатель имеют разные знаки. Поэтому полученное неравенство равносильно совокупности двух следующих систем неравенств: и Это означает, что решение исходного неравенства состоит из решений каждой из этих систем.

Решим первую систему неравенств, получим Очевидно, что решений нет (неравенства противоречивы). Решим вторую систему неравенств, получим то есть .

Говорят, что даны неравенств, если требуется найти значения , которые удовлетворяют, хотя бы одному из данных неравенств. Совокупность неравенств обозначают: или

Совокупность неравенств есть дизъюнкция неравенств или .

Аналогично определяют системы и совокупности неравенств со знаками , .

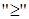Область определения совокупности (дизъюнкции) неравенств есть множество .

Решением совокупности неравенств с одной переменной называют всякое значение , которое обращает в истинное числовое неравенство хотя бы одно из неравенств совокупности.

Пример. Решим совокупность неравенств:

Решение. Данная совокупность неравенств равносильна следующей:

откуда находим, что решением заданной совокупности служит интервал .