Сумматоры

Сумматор представляет собой комбинационное цифровое устройство (КЦУ), предназначенное в основном для суммирования двоичных чисел. Кроме того, с помощью сумматора могут выполняться вычитание, умножение, деление, преобразование чисел в дополнительный код и некоторые другие операции. Обычно сумматор состоит только из логических элементов, а результат операции направляется затем для записи в регистр.

Классификация сумматоров может быть проведена по трем основным признакам:

числу входов (полусумматоры, одноразрядные и многоразрядные сумматоры). Многоразрядные сумматоры, в свою очередь, подразделяются на последовательные и параллельные; последние по способу организации межразрядных переносов подразделяются на сумматоры с последовательным и параллельным переносом и с групповой структурой;

способу тактирования (синхронные и асинхронные сумматоры);

системе счисления (двоичные, двоично-десятичные и др.).

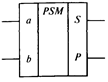
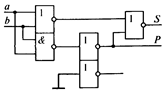
Полусумматорами (рис. 4.8, 4.9) называют КЦУ с двумя входами (а, b)и двумя выходами, на одном из которых вырабатывается сигнал суммы (выход S),а на другом – сигнал переноса (выход Р).Табл. 4.5 является таблицей истинности полусумматора.


Рис. 4.8. Условное обозначение полусумматора	Рис. 4.9. Схема полусумматора на логических элементах

Таблица 4.5

Таблица истинности полусумматора

а	b	S	P

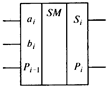
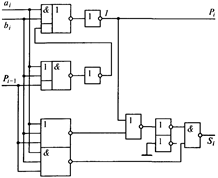
Одноразрядным сумматором (рис. 4.10, 4.11) называют КЦУ с тремя входами и двумя выходами. Кроме двух входов для чисел он имеет третий вход, на который подается сигнал переноса из предыдущего разряда. Одноразрядный сумматор является основным элементом многоразрядных сумматоров. Он выполняет арифметическое сложение одноразрядных двоичных чисел a_i и b_i и перенос P_i_-₁ из предыдущего разряда с образованием на выходе суммы S_i и переноса P_i в старший разряд (табл. 4.6).

Аналогичным способом могут быть построены логические схемы вычитателей. Как сумматоры, так и вычитатели предназначены для выполнения основных арифметических операций – сложения и вычитания. Имея на входе дополнительные средства для изменения знака второго аргумента, сумматор может прибавлять к первому слагаемому второе с измененным знаком,
т.е. вычитать, а вычитатель – вычитать из уменьшаемого вычитаемое с измененным знаком, т.е. прибавлять. Таким образом, в арифметико-логических устройствах (АЛУ) в большинстве случаев используется только один из двух рассматриваемых узлов, традиционно – именно сумматор, хотя по всем показателям вычитатель подобен сумматору.


Рис. 4.10. Условное обозначение одноразрядного сумматора	Рис. 4.11. Схема одноразрядного сумматора на логических элементах

Таблица 4.6

Таблица истинности одноразрядного сумматора

а_i	b_i	P_i-₁	S_i	P_i

Операции сложения и вычитания бывают последовательными и параллельными. В данном случае под последовательностью понимается поочередное, разряд за разрядом, сложение (или вычитание) на одноразрядной схеме с задержкой переносов (или займов) для использования их как третьих аргументов в следующем такте, т. е. в разряде.

При параллельных сложениях (или вычитаниях) используются столько одноразрядных сумматоров (или вычитателей), сколько разрядов в исходных числах (точнее – сколько разрядов в самом большом из них числе). Эти одноразрядные сумматоры взаимодействуют между собой по цепям переносов (или займов). Очевидно, что полный параллелизм при этом не достигается, так как переносы и займы распространяются с некоторой, хотя и небольшой, задержкой от младших разрядов к старшим. Имеется в виду схемное распространение займа в отличие от логического, направленного в противоположную сторону. Проблема сокращения времени распространения переносов (или займов) по разрядам – одна из главных при проектировании АЛУ.

Отметим некоторые особенности логики работы сумматоров и вычитателей:

сумма равна 1, если единичные значения принимает нечетное число аргументов;

выходной перенос равен 1, если единичные значения принимают больше двух аргументов;

разность равна 1, если при отсутствии входного займа из 1 вычитается 0 или из 0 вычитается 1; она также равна 1, если аргументы равны при наличии входного займа;

выходной заем равен 1, если из 0 вычитается 1, а также если аргументы равны при наличии входного займа.

В структуре АЛУ часто присутствует накопительный блок, состоящий из комбинационного сумматора (или вычитателя) и регистра результата. Подобный блок необходим при реализации последовательного алгоритма вычислений, когда вновь поступающий аргумент прибавляется к ранее накопленному результату или из него вычитается, а новый результат вычислений заменяет исходный.

Функцию накопительного блока, сочетающего функции сумматора (или вычитателя) и регистра, может выполнять набор Т-триггеров, работающих в режиме инверсии состояния, т.е. сложения по модулю 2. Такой сумматор на основе T-триггеров называют накопительным.Он уже является не комбинационным устройством, а конечным автоматом, поскольку обладает памятью.

Операции сложения (или вычитания) с учетом переноса (или займа) выполняются всегда над тремя аргументами, поэтому накопительный сумматор (или вычитатель) должен содержать управляющие коммутационные схемы, чтобы разнести сложение (или вычитание) на два такта. В этом состоит главный его недостаток. В остальном накопительный сумматор (или вычита-
тель) – самый простой и экономичный. Помимо несложных коммутационных схем он содержит дополнительно только цепи переноса (или займа).

Булевы функции, описывающие работу одноразрядного двоичного сумматора (по табл. 4.6), можно записать в следующем виде:

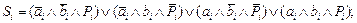
Используя различные варианты преобразования этих функций, можно реализовать большое число структур одноразрядных двоичных сумматоров (например по схеме, показанной
на рис. 4.12).

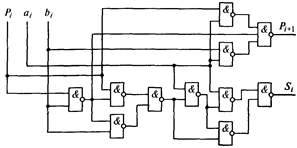
Рис. 4.12. Схема одноразрядного двоичного сумматора

Для обработки многоразрядных чисел объединяется соответствующее число одноразрядных сумматоров. При этом отдельные разряды обрабатываемых чисел А и В подаются на входы a_i и b_i. На вход P_i подается перенос из предыдущего, более младшего разряда. Формируемый в данном разряде перенос P_i₊₁ передается в следующий, более старший разряд. Такая организация процесса формирования переноса, называемая последовательным переносом, снижает быстродействие многоразрядного сумматора, так как получение результата в старшем разряде сумматора обеспечивается только после завершения распространения переноса по всем разрядам. Поэтому иногда организуется параллельный перенос.