Малая теорема Ферма, кольца вычетов.
№1 Кольца и поля вычетов
Преступим, в начале, к построению кольца вычетов  . И так пусть
. И так пусть  - множество целых чисел, тогда обозначим символом
- множество целых чисел, тогда обозначим символом  фактор множество множества
фактор множество множества  по отношению сравнимости по модулю
по отношению сравнимости по модулю 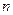 .(то есть
.(то есть  это множество классов эквивалентности таких, что два элемента
это множество классов эквивалентности таких, что два элемента 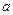 и
и 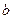
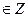 принадлежат данному классу тогда и только тогда когда
принадлежат данному классу тогда и только тогда когда  - целое число, или
- целое число, или 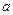 и
и 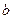 дают одинаковый остаток при делении на
дают одинаковый остаток при делении на 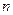 ). Обозначим за
). Обозначим за  класс эквивалентности содержащей число
класс эквивалентности содержащей число 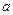 . Тогда множество
. Тогда множество  .Очевидно
.Очевидно  ,
,  . Докажем, что отношение сравнимости по модулю
. Докажем, что отношение сравнимости по модулю 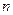 согласовано с операциями сложения и умножения.
согласовано с операциями сложения и умножения.
Очевидно: Если 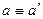 и
и 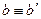 , то
, то 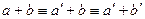 и
и  это означает, что можно в множестве
это означает, что можно в множестве  определить операции
определить операции 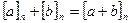 и
и  . Докажем что
. Докажем что  коммутативное ассоциативное кольцо с единицей.
коммутативное ассоциативное кольцо с единицей.
Действительно: 1) 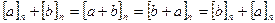 коммутативность.
коммутативность.
2) 
 ассоциативность.
ассоциативность.
3)  особая роль нуля.
особая роль нуля.
4)  докажем что
докажем что 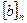 существует: Пусть
существует: Пусть 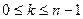 и
и  , тогда
, тогда 
 и
и 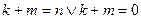 , так как для
, так как для 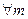 определённого выше
определённого выше 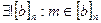 , то утверждение очевидно.
, то утверждение очевидно.
5) 
6) 
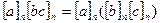
7) 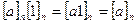
8) 

Докажем, что  есть поле, тогда и только тогда, когда
есть поле, тогда и только тогда, когда  простое число.
простое число.
Необходимость: Поведём от противного, пусть  , тогда
, тогда 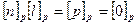 , если
, если  - поле все элементы обратимы, а значит
- поле все элементы обратимы, а значит 


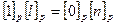

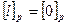 что противоречат условию.
что противоречат условию.
Достаточность: Пусть  простое число и
простое число и  докажем что
докажем что 

Умножим 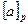 на все элементы кольца получим
на все элементы кольца получим 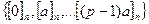 причём все они различны действительно если б
причём все они различны действительно если б 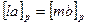 , то
, то 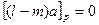 чего не может быть так как
чего не может быть так как  простое число, но значит среди
простое число, но значит среди 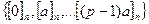 обязательно найдётся такое
обязательно найдётся такое 

Важно отметить, что в поле  имеет место, следующее равенство:
имеет место, следующее равенство: 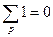
Число  называют характеристикой поля
называют характеристикой поля  , обозначают
, обозначают  .
.
Очевидно, что в поле  для
для 
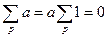 .
.
№2 Малая теорема Ферма
Лемма: В поле  для
для 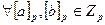 , справедливо соотношение
, справедливо соотношение 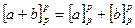 .
.
Доказательство: Очевидно,  , рассмотрим подробнее выражение
, рассмотрим подробнее выражение 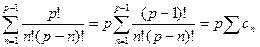 где
где 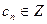 , тогда учитывая, что
, тогда учитывая, что  и
и  получим
получим 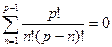 , откуда и следует утверждение леммы.
, откуда и следует утверждение леммы.
Теорема(Ферма): В поле  для
для  справедливо равенство:
справедливо равенство: 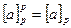 (
(  )
)
Доказательство: Из леммы очевидна следующая цепочка равенств:
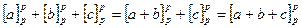 , и так далее имеем:
, и так далее имеем:  , положим
, положим 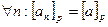 и
и  , получим:
, получим:  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.