Методы оптимальных решений
В задаче определения условного экстремума уравнения 
,х2, ……….х𝑛)= 0,1=1,2…., m,m<n называют: уравнение связи
Выбор наилучшего решения множества вариантов производства, распределения или потребления, осуществляется с помощью оптимизационных моделей
Венгерский метод применяется при решении задач целочисленного программирования
В транспортной задаче цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, остальные – в заполненных, называется циклом пересчета
Вследствие повышения цен на яблоки кривая спроса на груши сдвигается вправо
В транспортной задаче, где m – число поставщиков, n – число потребителей, количество переменных, подлежащих нахождению равно: m * n
В теории графов для любого дерева с m вершинами и n ребрами выполняется соответствие: m = n – 1
В транспортной задаче открытого типа имеется 3 поставщика и 5 потребителей некоторого однородного груза. Чтобы план перевозок не был вырожденным, число занятых клеток в таблице поставок должно быть равно: 8
В теории графов, связный без циклов называется: деревом
В задачах линейного программирования (при использовании геометрических построений) линия уровня 
: в направлении противоположном направлению вектора 
В модели Солоу устойчивый рост объема выпуска расчете на одного занятого объясняется: технологическим прогрессом
В задачах линейного программирования вектор переменных Х, удовлетворяющий системе ограничений задачи, называют: допустимым.
В модели межотраслевого баланса основой информационного обеспечения является: технологическая матрица.
В статистических межотраслевых моделях не используются: межотраслевые потоки капитальных вложений
В схеме межотраслевого баланса количество квадрантов равно: 4
Вектор Х=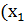 
,х2, ………. 
)являющийся решением системы
и содержащий лишь неотрицательные компоненты, называется: допустимым
Вектор Х= 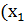,х2, ………. )являющийся решением системы
называется допустимым, если для любых j=1,2, ……n выполняется: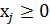 
В многоканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведением интенсивность потока заявок p=λ/m удовлетворяет условие : p/n<1
В модели межотраслевого баланса матрица А является матрицей коэффициентов прямых материальных затрат
Величины конечной продукции в модели межотраслевого баланса Леонтьева находится по формуле: Y=(Е – А) Х
В модели международной торговли (линейной модели торговли) АХ – Х = 0, матрица А – это: структурная матрица торговли
Вектор Х= 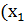,х2, ………. )являющийся решением системы
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
и удовлетворяющую условие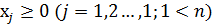 
при котором линейная функция F= 
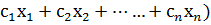принимает максимальное или минимальное значение, называется: оптимальным решением
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность потока заявок составляет 5 вызовов в минуту, а среднее время обслуживания одной заявки 10 секунд, среднее время пребывания заявки в системе равно: одна минута
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность потока заявок составляет 5 вызовов в минуту, а среднее время обслуживания одной заявки 10 секунд. Среднее число заявок в очереди равно 4
В одноканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведенная интенсивность потока заявок p=λ/m: p<1
Величины валовой продукции в модели межотраслевого баланса Леонтьева находятся по формуле: Х=(Е-А) 
Для полуплоскости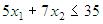 
точка А(3; 7) является внешней точкой.
Модель, соответствующая задаче нахождения переменных 
, удовлетворяющих системе неравенств (уравнений) 
( 
) где 
( 
),обращающих в максимум (или минимум) функцию 
, называется: задачей целочисленного программирования.
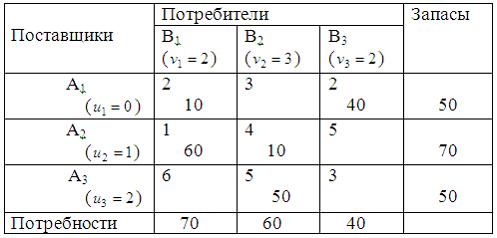
Для улучшения опорного плана транспортной задачи цикл пересчета следует построить для клетки: (3; 3).
Дана задача линейного программирования
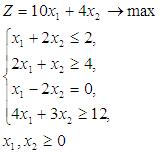
Ограничения на искомые переменные двойственной задачи имеют вид:
Модели, которые используют такие наглядные элементы, как упругие шары, потоки жидкости, траектории движения тел, относятся к: образным.
Моделирование, в котором изучаются модели, предназначенные для воспроизведения динамики процессов, происходящих в изучаемом объекте, причем общность процессов основывается на сходстве их физической природы, называется физическим.
Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется: канонической.
При решении задачи целочисленного программирования методом Гомори при необходимости вводится дополнительное ограничение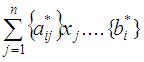 
. Вместо многоточия следует поставить знак 
Методом целочисленного программирования требуется решать задачу о назначении
Выбор наилучшего решения из множества вариантов производства, распределения или потребления, осуществляется с помощью: оптимизационных моделей
Параллельными ребрами в графе называются ребра имеющие одинаковые концевые вершины
Если в транспортной задаче объем потребностей превышает объем запасов, в рассмотрение вводят: один фиктивный пункт производства.
Методом рекуррентных соотношений решается задача динамического программирования
Задача линейного программирования при условии максимизации целевой функции имеет оптимальное решение, если допустимое множество решений не пусто и ограничено сверху
Сетевой график задачи СПУ (сетевого планирования и управления) имеет четыре полных пути. Их длины: 
, 
, 
, 
.
Наибольшим полным резервом времени обладает второй путь.
Сетевой график задачи СПУ (сетевого планирования и управления) имеет четыре полных пути. Их длины: , , , .
Длина критического пути равна 41.
Уравнение Беллмана (рекуррентное соотношение) для задачи загрузки рюкзака имеет вид: 
При анализе случайных процессов с дискретными состояниями удобно пользоваться графом состояний.
Рентабельной является продукция, для которой дополнительная двойственная переменная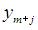 
в оптимальном плане задачи: 
Поиск разрешающего элемента в симплекс-таблице при решении задачи линейного программирования симплексным методом начинается с…
выбора разрешающего столбца.
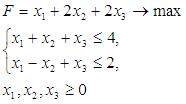
Оптимальным в данной задаче линейного программирования является вектор X = (0; 4; 0)
Вероятность отказа в обслуживании заявок в многоканальной СМО равна 0,2. Приведенная интенсивность потока требований ( 
) – 5. Среднее число занятых каналов равно 4.
Дана задача линейного программирования
Двойственной по отношению к данной является задача
Случайный процесс называется Марковским, если это: процесс без последствий.
return false">ссылка скрыта· Граф, ребрами которого являются всевозможные пары для двух различных вершин, называют полным.
· Граф может быть задан: матрицей, списком, рисунком.
· Граф, в котором движение по дугам возможно в любом направлении, называют неорентированным.
· Граф, в котором любая пара вершин связана, называют связным.
· Вторая теорема двойственности: для того чтобы x y были оптимальными для пары двойственных задач
и 
Должны выполняться соотношения:
В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит непроверенной. Среднее число деталей поступающих в ОТК в течении часа равна 24, среднее время, которое затрачивает один контролер на обслуживание одной детали, равно 5 мин.
Вероятность простоя каналов обслуживания 
:
0,1579
В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает один контролер на обслуживание одной детали, равна 5 мин.
Вероятность отказа в обслуживании 
: 0,21
В теории графов для любого дерева с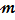 
вершинами и 
ребрами выполняется соотношение:
В теории графов связный граф без циклов называется: деревом
В задаче определения условного экстремума уравнения 
называют: уравнения связи
В транспортной задаче, где 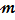- число поставщиков, - число потребителей, количество переменных подлежащих нахождению равно: 
В транспортной задаче цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, остальные – в заполненных называется: циклом пересчета
Вследствие повышения цен на яблоки кривая спроса на груши…
сдвигается вправо
Венгерский метод применяется при решении задач
целочисленного программирования
Выбор наилучшего решения из множества вариантов производства, распределения или потребления, осуществляется с помощью:
оптимизационных моделей
В задачах линейного программирования (при использовании геометрических построений) линия уровня 
достигает низшего уровня, передвигаясь:
в направлении, противоположном направлению вектора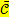 
=( 
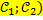
В модели Солоу устойчивый рост объема выпуска в расчете на одного занятого объясняется:
технологическим процессом
В задачах линейного программировния вектор переменных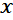 
, удовлетворяющий системе ограничений задачи, называют: допустимым
Вектор 
, являющийся решением системы
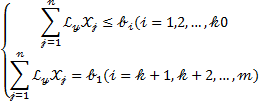
Называется допустимым, если для любых 
выполняется: 
В транспортной задаче открытого типа имеется 3 поставщика и 5 потребителей некоторого однородного груза. Чтобы план перевозок не был вырожденным, число занятых клеток в таблице поставок должно быть равно: 8
Вектор 
являющийся решением системе
и удовлетворяющие условию 
, при котором линейная функция
принимает максимальное или минимальное значение, называется:
оптимальным решением
Вектор 
, являющийся решением системы:
И содержащий лишь неотрицательные компоненты, называются: допустимым
Величины конечной продукции в модели межотраслевого баланса Леонтьева находятся по формуле:
В статистических межотраслевых моделях не используются:
межотраслевые потоки капитальных вложений
В схеме межотраслевого баланса основой информационного обеспечения является:
технологическая матрица
В схеме межотраслевого баланса количество квандрантов равно: 4
В модели межотраслевого баланса матрица А является матрицей:
коэффициентов прямых материальных затрат
В модели международной торговли (линейной модели торговли) 
матрица А – это:
структурная матрица торговли
Величины валовой продукции в модели межотраслевого баланса Леонтьева находятся по формуле:
Вектор Х=(1;2;0)является оптимальным в задаче линейного программирования
+ 
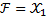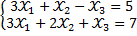
Оптимальным в двойственной задаче является вектор:
В многоканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведенная интенсивность потока заявок 
удовлетворяет условию:
В двухканальной системе массового обслуживания интенсивность потока заявок составляет 5 вызова в минуту, а время обслуживания 0,4 минуты. Вероятность простоя каналов обслуживания равна: 0,2
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность потока заявок составляет 5 вызовов в минуту, а среднее время обслуживания одной заявки 10 секунд. Среднее время пребывания заявки в системе равно: одна минута
В одноканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведенная интенсивность потока заявок
Вектор Х= (3;0,2) является оптимальным в задаче:
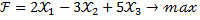
Оптимальным вектором двойственной задачи является:
В многоканальной СМО с неограниченной длиной очереди вероятность того, что в системе нет заявок 
вычисляется по формуле: 
100 т некоторого продукта могут быть произведены при следующих комбинациях факторов производства:
| Единицы первого фактора (труд) | 10 | 6 | 3 | 1 |
| Единицы второго фактора (капитал) | 2 | 7 | 13 | 16 |
Цена единицы первого фактора составляет 100ДМ, второго – 60 ДМ. Наиболее предпочтительной является комбинация: (10;2)
50 т некоторого продукта могут быть произведены при следующих комбинациях факторов производства:
| Единицы первого фактора (труд) | 10 | 6 | 3 | 1 |
| Единицы второго фактора (капитал) | 2 | 7 | 13 | 16 |
Цена единицы первого фактора составляет 120 ДМ, второго – 50 ДМ. Наиболее предпочтительной является комбинация: (1;16)
Алгоритм решения задачи линейного программирования:
1 – находим область допустимых решений системы ограничения задачи
2 – строим вектор – график целевой функции
3 – проводим линию уровня
4 – находим точку экстремума
5 – находим экстремальное значение целевой функции
Абсолютная пропускная способность СМО вычисляется по формуле:
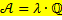
Базисное распределение поставок (опорный план) оптимального тогда и только тогда, когда оценки всех свободных клеток, определяемые по формуле: 
неположительны
Более одного цикла содержит граф:
Уравнение бюджетной линии имеет вид 
Наклон бюджетной линии
-2
Увеличение реального дохода в экономике или рост реального выпуска в расчете на душу населения – это: экономический рост
0 7 
Уравнение линии бюджетного ограничения, изображенной на рисунке имеет вид:
Уравнение, где достигается наибольшее возможное значение переменной,
переводимой в основные, называется: разрешающее
Увеличение реального дохода в экономике или рост реального выпуска в расчете на душу населения – это экономический рост.
Уравнения Беллмана используются при решении: задач динамического программирования
Условию продуктивности для модели Леонтьева удовлетворяет матрица: 
Уравнение Беллмана (рекуррентное соотношение) для задачи распределения средств между предприятиями имеет вид: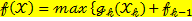 
( 
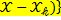
Уравнение модели межотраслевого баланса имеет вид: 
Уравнение модели международной торговли (линейной модели торговли) имеет вид: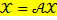 
Уравнение Беллмана (рекуррентное соотношение) для задачи загрузки рюкзака имеет вид:
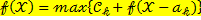
Методом рекуррентных соотношений решается: задача динамического программирования
Методы оптимизации, в которых процесс принятия решений является многошаговым, относится к:
динамическому программированию
Метод решения транспортных задач в матричной постановке называется методом: потенциалов
Матрицу межотраслевых материальных связей в модели межотраслевого баланса составляет квадрат № 1
Модификация симплексного метода применительно к транспортной задаче называется: распределительный метод
Матрица коэффициентов системы ограничений двойственной задачи по отношению к матрице коэффициентов прямой задачи А находится следующим образом: 
Методом множителей Лагранжа решаются задачи: нелинейного программирования
Множество планов основной задачи линейного программирования является: выпуклым
Модели, которые воспроизводят закономерности во времени и устанавливают функциональную зависимость между неизвестными значениями переменных и временем называются: динамическими
Модели, в которых все величины определяются на отрезках времени в целом или на конец рассматриваемого периода, называется: статическими
Метод решения транспортных задач в матричной постановке называется методом: потенциалов
Моделирование, в котором изучаются модели, предназначенные для воспроизведения динамики процессов, происходящих в изучаемом объекте, причем общность процессов основывается на сходстве их физической природы, называется: физическим
Модели, требующие соответствия наличия ресурсов и их использования, называется: балансовыми
Моделирование, использующее материальные модели, имеющие другую физическую природу, но описывающиеся теми же математическими соотношениями, что и изучаемое явление или объект, называется: аналоговым
Модель, соответствующая задаче нахождения переменных 
удовлетворяющие системе неравенств (уравнений) 
, 
где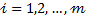 
и обращающих в максимум (или минимум) целевую функцию 
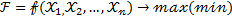называется: оптимизационной
Модель, в которой характеристики объекта моделирования описываются с помощью математических выражений, называется: формализованной
Модели, отображающие лишь поведение объекта, называют: функциональными
Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой неравенств, называется: стандартной
Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется: кононической
При стабильной цене на автомобильные шины цена на автомобили увеличивается, при этом: уменьшается количество покупаемых шин
При неизменной цене на маргарин растет цена на сливочное масло, при этом: спрос на маргарин увеличивается
При моделировании экономических процессов методами сетевого планирования и управления пользуются понятиями резервов времени событий. К какому виду резерва относится резерв, соответствующий случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие – начинаются в ранние сроки: свободный резерв времени
При моделировании экономических процессов методами сетевого планирования и управления пользуются понятиями резервов времени событий. К какому виду резерва относится резерв, показывающий, на сколько можно увеличить время выполнения конкретной работы, не изменив при этом раннего срока ее конечного события: полный резерв времени
В задачах динамического программирования (о рюкзаке) при заполнении таблицы
| 
| 
| … | 
|
| 
| 
| … | 
|
| 
| 
| … | 
|
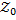
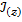
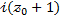
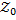- означает
(минимальный вес)
В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает один контролер на обслуживание одной детали, равна 5 мин. Доля заявок, обслуженных систем 
0,79
В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает один контролер на обслуживание одной детали, равна 5 мин. Абсолютная пропускная способность (А): 18,96
В задачах динамического программирования (о рюкзаке) при заполнении таблицы
|
|
|
| … | 
|
|
|
|
| … | 
|
|
|
|
| … | 
|
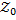
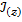
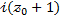
?- означает
(грузоподъемность)
В оптимизационной задаче критерий эффективности количественного выражения в виде: целевой функции
В процессе динамического программирования раньше всех планируется: последний шаг
В задаче динамического программирования уравнение вида 
называется : уравнением состояний
В задаче динамического программирования уравнения вида
Уравнение Беллмана
В задачах динамического программирования шаговое управление должно выбираться: с учетом последствий в будущем.
В качестве шага при решении задачи динамического программирования нельзя рассматривать: стоимость оборудования.
В задаче о загрузке рюкзака при заполнении таблицы
|
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
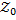
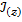
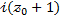
?- означает
(грузоподъемность)
В задаче о загрузке рюкзака при заполнении таблицы
|
|
|
| … |
|
|
|
|
| … | 
|
|
|
|
| … |
|
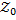
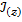
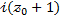
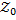- означает
( минимальный вес)
означает (грузоподъемность)
Задача определения такого допустимого управления Х, переводящего систему 
из состояния 
в состояние 
, при котором целевая функция
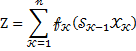
Принимает наибольшее (наименьшее) значение – это
задача динамического программирования
Задача о загрузке рюкзака является задачей динамического программирования.
Задачи о назначениях решаются: венгерским методом.
Зависимость издержек производства от объема выпускаемой продукции выражается формулой
Средние издержки при объеме продукции 
ден.ед. равны 24
Зависимость между себестоимостью продукции и объемом ее производства выражается формулой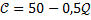 
, эластичность себестоимости при выпуске продукции 
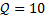равна -0,11
За определенный период времени потребитель покупает 10 кг свинины по цене 250 рублей за кг, а по цене 220 рублей он покупает 11 кг свинины. Эластичность спроса удовлетворяет условию:
Задача линейного программирования, в которой все переменные неотрицательны и система ограничений состоит из одних уравнений, называется: Кононической. Общей.
Задача линейного программирования имеет множество оптимальных решений, если целевая функция принимает максимальное (минимальное) значение:
в любой точке одной из сторон многоугольника решений.
Задача, решаемая симплексным методом, должна быть записана в форме: канонической.
Задачи с логистическими переменными относятся к задачам:
целочисленного программирования.
Задача линейного программирования, в которой все переменные неотрицательны, а система ограничений состоит лишь из одних неравенств, называется: стандартной.
Задача линейного программирования имеет единственное оптимальное решение, если целевая функция принимает максимальное (минимальное) значение в одной из:
угловых точек многогранника решений.
Задача линейного программирования может достигать максимального значения:
в одной или во множестве точек.
Дана последняя симплексная таблица решения задачи линейного программирования
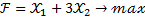
| Базис | 
| 
| 
| 
| 
|
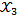
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Чему будет равно значение 
оптимального плана задачи, если ресурс первого вида увеличить на 1 условную единицу? 15/13
Дана последняя симплексная таблица решения задачи линейного программирования
|
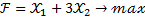
| Базис |
|
|
|
|
|
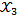
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Чему будет равно значение 
оптимального плана задачи, если ресурс первого вида увеличить на одну условную единицу? 40/13
Дана последняя симплексная таблица решения задачи линейного программирования
|
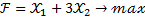
| Базис |
|
|
|
|
|
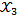
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Оптимальный план двойственной задачи:
(12/13; 5/13; 0; 0)
Дана последняя симплексная таблица решения задачи линейного программирования
|
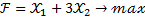
| Базис |
|
|
|
|
|
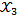
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Значение оптимального плана задачи при увеличении 
на одну условную единицу будет равно
20/13
Дана последняя симплексная таблица решения задачи линейного программирования
|
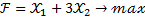
| Базис |
|
|
|
|
|
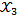
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Значение оптимального плана задачи при увеличении на одну условную единицу будет равно 36/13
Дана последняя симплексная таблица решения задачи линейного программирования
|
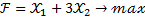
| Базис |
|
|
|
|
|
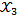
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Максимальное значение целевой функции задачи при увеличении на одну условную единицу будет равно 128/13
Дана последняя симплексная таблица решения задачи линейного программирования
|
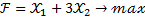
| Базис |
|
|
|
|
|
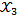
| 1 |
| 35/13 | 0 | 1 | 5/13 | 1/13 |
| 2 |
| 18/13 | 1 | 0 | -3/13 | 2/13 |
| 3 | 123/13 | 0 | 0 | 12/13 | 5/13 |
Максимальное значение целевой функции задачи при увеличении 
на одну условную единицу будет равно 135/13
| Поставщики | потребители | запасы | ||
| 
| 
| ||
| 2 | 3 10 | 2 40 | 50 |
| 2 70 | 4 | 5 | 70 |
| 6 | 5 50 | 7 | 50 |
| Потребности | 70 | 60 | 40 |
Для транспортной задачи не соответствует действительности утверждение о том, что:
опорный план является единственным
опорный план является невыраженным
| Поставщики | потребители | запасы | ||
|
|
|
| ||
|
| 2 | 3 10 | 2 40 | 50 |
|
| 2 70 | 4 | 5 | 70 |
|
| 6 | 5 50 | 7 | 50 |
| Потребности | 70 | 60 | 40 |
Дана транспортная задача опорный план задачи является:
выраженным допустимым
| Поставщики | потребители | Мощность поставщиков | ||
|
|
|
| ||
|
| 2 15 | 3 | 2 35 | 50 |
|
| 2 55 | 4 15 | 5 | 70 |
|
| 6 | 5 45 | 7 5 | 50 |
| Спрос потребителей | 70 | 60 | 40 |
Предложенный план транспортной задачи является: не является опорным.
Дана матрица смежности для некоторого графа. Количество ребер графа равно: 9
| 
| 
| 
| 
| |
|
| 0 | 0 | 2 | 1 | 0 |
|
| 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 1 |
|
| 1 | 0 | 1 | 1 | 0 |
|
| 0 | 1 | 1 | 0 | 0 |
Дана матрица смежности для некоторых графа. Количество параллельных ребер равно: 2