ГРАФИЧЕСКИЕ МЕТОДЫ ПОИСКА ОПТИМАЛЬНОГО РЕШЕНИЯ ЛИНЕЙНЫХ МОДЕЛЕЙ

ЦЕЛЬ РАБОТЫ: развить навыки анализа экономико-математических моделей на основе графических методов поиска их оптимальных решений.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ. Возможны различные подходы к анализу линейных оптимизационных моделей. Однако наиболее наглядным и простым способом является геометрическая интерпретация линейной модели и всех ее элементов.

Для построения графического аналога линейной оптимизационной модели необходимо выбрать систему координат. Наиболее удобной для этой цели является прямоугольная декартовая система координат, где каждой управляющей переменной x_j, j = 1, n соответствует своя ось. В наиболее простом случае – это плоскость с двумя координатными осями. Важно помнить, что все свойства модели, характерные для 2–х и 3–х мерных моделей, полностью сохраняют свои свойства и для n–х пространств и моделей.

Для того чтобы лучше понять методику анализа линейной оптимизационной модели на основе геометрической интерпретации, рассмотрим простейшую модель, включающую в себя функцию двух переменных:

z₀ = p₁x₁ + p₂x₂ → max;

y_r = – a_r₁ – a_r₂x₂ + a_r ≥ 0, r = 1, k;

y_l = a_l₁x₁ + a_l₂x₂ – a_l ≥ 0, l = k + 1, m;

x₁ ≥ 0, x₂ ≥ 0.

При построении осей для 2-мерной модели, как правило, по горизонтали откладывают объем услуг1-го вида. По вертикальной оси - объем услуг2-го вида. Таким образом, каждая точка на плоскости является программой оказания обоих видов услуг, а координаты этой точки определяют конкретный объем оказания услуг 1-го и 2-го вида.

Геометрический смысл целевой функции z₀= p₁x₁ + p₂x₂ – прямая, которая проходит перпендикулярно к нормальному вектору p с координатами p = (p₁, p₂). Этим вектором фиксируется направление прямой (p₁x₁ + p₂x₂) относительно координатных осей. При z₀ = 0 эта прямая проходит через начало координат. Экономический смысл этой прямой заключается в том, что прямая z₀= 0 определяет множество возможных вариантов программ, суммарная прибыль для которых равна нулю. Направляющий вектор

p = (p₁, p₂) показывает, где лежат точки (программы) с положительным значением прибыли z₀ > 0. В противоположном направлении расположены точки (программы) с отрицательным значением суммарной прибыли z₀ < 0 (убытки).

Все остальные прямые, соответствующие уравнениям y_r и y_l, строятся по двум точкам. Для этого попеременно приравнивается нулю x₁ и x_2.

Геометрический смысл переменной y_r – прямая, не проходящая через начало координат, так как a_r ≠ 0. Прямая y_r проходит перпендикулярно вектору A_r = (-a_r₁, -a_r₂) с отрицательными координатами. Экономический смысл этой прямой при y_r = 0 состоит в том, что на ней лежат все программы по оказанию услуг, для которых экономия r-го производственного ресурса равна нулю, т.е. фонды (лимиты) по этому ресурсу израсходованы. Вектор

A_r = (-a_r₁, -a_r₂) показывает, в каком направлении лежат точки (программы) с большей экономией r-го ресурса, ниже - его перерасхода.

Геометрический смысл переменной y_l - прямая, не проходящая через начало координат, так как контрольные цифры программы (плана) отличны от нуля, то есть a_l ≠ 0. На этой прямой лежат все точки (программы), для которых перевыполнение плана по l-му экономическому показателю равно нулю. Другими словами, программа по оказанию услуг выполняется на 100%.

Направляющий вектор A_l = (a_l₁, a_l₂) показывает область, где планы по выполнению услуг перевыполняются y_l > 0, или составляют более 100%. В противоположном направлении лежат планы, для которых задание по l-му экономическому показателю y_l < 0, то есть не выполняется, или составляет менее 100%.

МТОДИКА ПОСТРОЕНИЯ ГРАФИЧЕСКОЙ МОДЕЛИ ЛИНЕЙНОГО ТИПА

1. Приравниваются к нулю каждая из переменных, входящих в модель. Эту процедуру начинают с управляющих переменных: x₁=0, x₂=0 – это две прямые, которые рассматриваются в качестве координатных осей (см. рис.1). Каждая точка плоскости, ограниченная штриховкой, является программой (планом) оказания услуг двух видов (x₁ и x₂).

y₂=0

y₄=0

X₁(x₂=0)

(4)

(1)

(2)

P₁

(3)

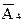
Рисунок 1 - Пример графического поиска и анализа оптимального

решения модели линейного типа

2. Приравнивается к нулю переменная z₀, и строится прямая z₀=0, перпендикулярная вектору p(p₁, p₂), направление которого показывает, в какую сторону следует изменять план.

3. Приравниваются к нулю переменные y₁ и y₂ (y_r₁и y_r₂) характеризующие экономию ресурсов. Строятся прямые y₁=0, y₂=0, перпендикулярные векторам A₁(- a₁₁, - a₁₂) и A₂(- a₂₂, - a₂₂). Направления векторов показывают, как следует изменить программу оказания услуг (или выпуска продукции), чтобы увеличить экономию ресурсов (см. рис.1).

4. Приравниваются к нулю переменные y₃ и y₄(y_l₁и y_l₂), характеризующие перевыполнение программы по экономическим показателям. Строятся прямые y₃=0, y₄=0, перпендикулярные векторам

A₃(- a₃₁, - a₃₂) и A₄(- a₄₁, - a₄₂). Направления векторов указывают, в какой области лежат программы по оказанию услуг, обеспечивающие рост экономических показателей.

5. На заключительном этапе анализа линейной модели отыскивается оптимальное решение. Для этого выделяется общая для всех переменных модели заштрихованная область. В общем случае – это многогранник, все точки которого представляют собой область допустимых решений.