Занятия 37 – 41. Координаты и векторы на плоскости и в пространстве.

Векторы на плоскости.

Определение 1. Вектором называется класс эквивалентности (по отношению равенства) направленных отрезков. Например, можем рассмотреть вектор с концами в точках : .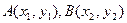

Сложение векторов:

1. правило треугольника;

2. правило параллелограмма;

3. правило ломаной.

Произведение вектора на число:

Свойства сложения и произведения векторов на число:

1.

2.

3.

4.

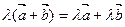
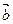Определение 2. Векторы и коллинеарны, если несущие их прямые параллельны или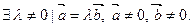

Теорема: Если , 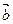не коллинеарны, то любой вектор 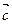может быть разложен по векторам , 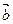единственным образом, т.е. существуют числа .

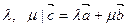Определение 3. Скалярное произведение векторов равно: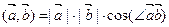

Определение 4. Векторы называются ортогональными, если их скалярное произведение равно нулю.

Свойства скалярного произведения:

1.

2.

3.

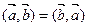
4.

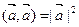
5.

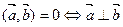
Теорема: Если 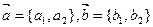, то .

Замечание: 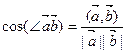, следовательно, если скалярное произведение векторов больше нуля, то угол между векторами – острый, если меньше нуля – тупой.

Уравнение прямой: 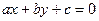или в другом виде:

Ø b = 0; x = - ,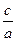

Ø b ≠ 0; y = kx + b, где k – угловой коэффициент или тангенс угла наклона прямой.

1. Две прямые параллельны, если их угловые коэффициенты равны, то есть k₁ = k₂.

2. Две прямые перпендикулярны, если произведение их угловых коэффициентов равно – 1, то есть k₁k₂ = -1.

3. Расстояние от точки М(А, В) до прямой 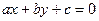равно .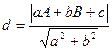

Задачи:

1.Даны векторы 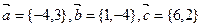. Разложите вектор 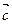по двум другим.

2. Даны векторы 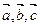. Докажите, что .

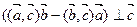3. Дан отрезок АВ и точка М на нем так, что . Выразите радиус-вектор точки М через радиус-векторы точек А и В для произвольного значени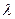я , для 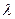, равного 1, 2, ½.

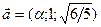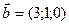4. Угол между векторами и равен 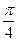. Найдите 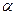. Базис прямоугольный.

5. На плоскости найдите точку, симметричную точке с координатами (2; 4) относительно прямой, заданной уравнением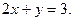

6. Найдите координаты точки, симметричной вершине параболы 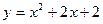относительно прямой 2у – 2х = 1.

Векторы в пространстве. Метод координат в пространстве.

Определение 1. Векторы 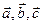называются компланарными, если существует такая плоскость, что все три вектора параллельны этой плоскости.

Утверждение 1. Если вектор 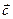можно разложить по векторам 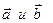, то есть представить в виде 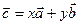, где х, у – некоторые числа, то векторы 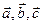компланарны. И наоборот, если векторы 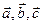- компланарные векторы, причём векторы 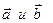не коллинеарны, то вектор 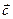можно представить в виде .

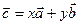Утверждение 2. Любой ненулевой вектор 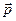можно разложить по трём данным некомпланарным векторам 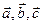, то есть представить в виде 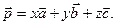Коэффициенты x, y, z определяются единственным образом.

Определение 2. Базис в пространстве – упорядоченная тройка некомпланарных векторов. Базис 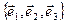называется ортонормированным, если векторы 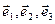попарно ортогональны и .

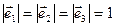Определение 3. Если в пространстве выбрана прямоугольная система координат и на положительных полуосях отложены единичные векторы 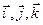, то любой вектор можно разложить по координатным векторам, то есть представить в виде , причём коэффициенты разложения определяются единственным образом. Числа x, y, z называют координатами вектора в данной системе координат и пишут .

Утверждение 3. Ненулевые векторы коллинеарны ( лежат на параллельных прямых ) тогда и только тогда, когда существует число k, не равное нулю такое, что .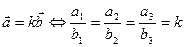

Утверждение 4. Расстояние d между точками 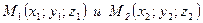равно длине вектора 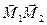, то есть 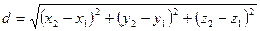. Координаты точки M(x; y; z), делящей отрезок М₁М₂ между точками 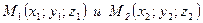в отношении 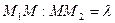, определяются формулами 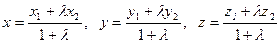. Если М – середина отрезка М₁М₂, то .

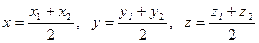Определение 4. Скалярное произведение векторов 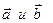, где , есть число 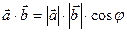, где - угол между векторами .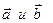

Утверждение 5. Скалярное произведение векторов 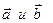может быть выражено через их координаты следующим образом: .

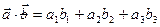1. Свойства скалярного произведения: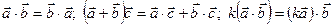

2. Косинус угла между прямыми, параллельными векторам 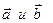может быть вычислен следующим образом: , векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Уравнения прямой в пространстве:

1. Параметрическое задание прямой, проходящей через точку M₀(x₀;y₀;z₀) параллельно вектору 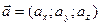, имеет векторный вид 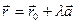, где 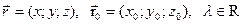, или скалярный – в виде системы из трех соотношений для трех координат произвольной точки прямой: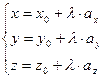

2. Это уравнение можно записать в виде: .

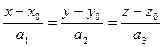3. Уравнение прямой, проходящей через точки 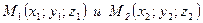, можно записать в виде .

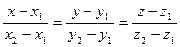Уравнение сферы радиуса R с центром в точке M₀(x₀;y₀;z₀) записывается в виде .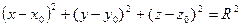

Уравнение плоскости.

Утверждение 6. Если , то в прямоугольной системе координат уравнение вида задаёт плоскость, перпендикулярную вектору 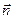, который называется вектором нормали для заданной плоскости.

Угол между плоскостями.

Утверждение 7. Если две плоскости в прямоугольной системе координат заданы уравнениями и , то угол между этими плоскостями равен углу между их нормалями, то есть

Эти плоскости перпендикулярны тогда и только тогда, когда , и параллельны тогда и только тогда, когда

Угол между прямой и плоскостью.

Утверждение 8. Если прямая параллельна вектору , плоскость в прямоугольной системе координат задана уравнением , - угол между прямой и плоскостью, то , где - угол между прямой и вектором нормали.

Расстояние от точки до плоскости.

Утверждение 9. Расстояние от точки М (А, В, С) до плоскости может быть вычислено следующим образом: .

Задачи начального уровня.

1. Составьте уравнение плоскости, проходящей через точки А(0,0,0), В(1,0,1), С(0,1,0).

2. Составьте уравнение плоскости, проходящей через точки А(0,1,5), В(3,0,1), С(-1,1,6).

3. Составьте уравнение плоскости, проходящей через точку А(1,-3,2) параллельно плоскости .

4. Составьте уравнение плоскости, проходящей через точку А(0,1,2) перпендикулярно вектору .

5. Составьте уравнение плоскости, проходящей через точку А(0,1,0) параллельно векторам и .

6. Составьте уравнение плоскости, проходящей через две точки А(1,2,-1) и В(-1,0,1) перпендикулярно плоскости .

7. Составьте уравнение плоскости, проходящей через две точки А(1,2,-1) и В(-1,0,1) параллельно вектору .

8. Найдите угол между плоскостями и

9. Найдите угол между прямой, проходящей через точки А(1,0,-1) и В(1,2,0) и плоскостью .

10. Найдите расстояние от точки А(1,1,1) до плоскости .

Параметрическое задание прямых. Расстояние между скрещивающимися прямыми.

Расстояние между прямыми есть длина общего перпендикуляра к этим двум прямым.

Алгоритм нахождения расстояния – координатно-векторный метод.

Пусть заданы в пространстве две прямые а и b. На них расположены соответственно векторы и точки, на прямой а: , на прямой b: . Используя параметрическую форму задания прямой, выпишем условия принадлежности точек P и Q прямым а и b:

и , где числа p, q – параметры, соответствующие месту расположения точек P, Q на прямых a, b. Если точки Р и Q движутся по прямым, вектор меняет своё положение в зависимости от значений параметров p, q. Условия перпендикулярности данного вектора векторам равносильно тому, что скалярные произведения соответствующих пар векторов равны нулю. При этом мы получаем систему из двух линейных уравнений с двумя неизвестными p, q, так как координаты вектора являются функциями от данных двух параметров.

return false">ссылка скрыта

После нахождения параметров p, q мы можем вычислить расстояние между прямыми как длину вектора при найденных значениях p, q, когда данный вектор является общим перпендикуляром к заданным прямым.

Скрещивающиеся прямые. Построение прямой, пересекающей две данные скрещивающиеся прямые.

1. Пусть нам требуется провести в пространстве прямую через заданную точку А, пересекающую две скрещивающиеся прямые а и с. Построим плоскость через точку А и одну из прямых, например, прямую а. Эта плоскость пересечёт вторую прямую с в некоторой точке С. Если мы проведём сейчас прямую через точки А и С в построенной плоскости, то эта прямая пересечёт прямую а в некоторой точке В, искомая прямая будет прямой ВС, которая проходит через точку А и пересекает обе прямые а и с.

2. Пусть нам требуется провести в пространстве прямую через заданную точку А, пересекающую две скрещивающиеся прямые а и с. Построим плоскость через точку А и одну из прямых, например, прямую а. Построим вторую плоскость через точку А и вторую прямую с. Обе эти плоскости пересекутся по прямой е, которая проходит через точку А и пересекает обе заданные прямые а и с. Это и будет искомая прямая.

Векторный метод работы с условиями коллинеарности и компланарности.

Мы можем работать с векторами без введения прямоугольной системы координат в случае наличия условий коллинеарности или компланарности некоторых данных векторов. Например, в случае работы с произвольными треугольными пирамидами, мы имеем три некомпланарных вектора, направленных вдоль рёбер тетраэдра из одной вершины: 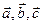. Расположение точки на некоторой прямой, ребре или другом известном направлении, может быть задано одним параметром. Разложение любого вектора, связанного с одной точкой, по базису некомпланарных векторов 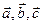будет зависеть также от одного этого параметра. Координаты вектора, связанного с двумя свободными точками, в разложении по базису 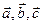будут зависеть таким образом, от двух параметров. Наличие условия коллинеарности вводит третий параметр – коэффициент пропорциональности координат. Наличие условия компланарности позволяет разложить один из четырёх векторов по трём другим, вводя три параметра разложения. Найти три неизвестных параметра в обоих из этих двух случаев мы можем, используя условие единственности разложения любого вектора по базису некомпланарных векторов.

 

Задачи для самостоятельной классной и домашней работы.

1. Дан куб ABCDA’B’C’D’. Точки М и К – середины ребер CC’ и A’D’ соответственно. Найдите угол между плоскостями ABCD и ВМК.

2. Дан куб ABCDA’B’C’D’. Точки М и К – середины ребер CC’ и A’D’ соответственно. Найдите угол между прямой МК и плоскостью ABCD.

3. Дан единичный куб ABCDA’B’C’D’. Точка Е расположена на ребре CC’ так, что CE = 2 C’E. Найдите расстояние от вершины А куба до плоскости B’D’E.

4. Дан куб ABCDA’B’C’D’. Через вершину А и середины ребер CC’ и A’D’ проведена плоскость. Найдите величину двугранного угла, образованного этой плоскостью и плоскостью основания.

5. В треугольной пирамиде SABC ребро SA перпендикулярно плоскости треугольника АВС, . Через середину ребра АС проведена плоскость, перпендикулярная ребру SB. Найдите расстояние от вершины А до этой плоскости.

6. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра АВ = 5, AD = 10, АА₁ = 2 . Найдите длину перпендикулярной проекции отрезка А₁В₁ на плоскость BМD, где М – середина ребра В₁С₁.

7. В единичном кубе ABCDA₁B₁C₁D₁ с основанием ABCD точка М – середина ребра СС₁. Найдите площадь ортогональной проекции грани ВВ₁СС₁ на плоскость ВD₁M.

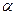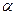8. В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 3, ВС = 2. Боковые ребра пирамиды имеют одинаковую длину, а ее высота равна 3. Плоскость параллельна SB и AC, плоскость параллельна прямым SC и BD. Определите величину угла между плоскостями и .

9. В основании треугольной пирамиды SABC лежит правильный треугольник АВС со стороной 2. Ребро SA перпендикулярно плоскости основания и . Точка К – середина ребра ВС. Плоскость 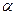параллельна прямым АВ и SC. Определите величину двугранного угла между прямой АК и плоскостью .

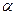10. В треугольной пирамиде SABC рёбра АВ, AC и AS взаимно перпендикулярны и АВ = 1, АС = 2, AS = 4. Точки К и L – середины рёбер BS и АС. Найдите угол между прямой KL и плоскостью BSC.

11. Прямоугольник ABCD cо сторонами АВ = 6, ВС = 9 является основанием прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ , боковые рёбра которого равны 3. На диагонали А₁С параллелепипеда выбрана точка Р так, что угол между векторами равен . Найдите отношение А₁Р:РС.

12. Дан куб с основанием ABCD и боковыми рёбрами АА’, ВВ’, СС’, DD’. Длина ребра куба равна 1. Точки М и N – середины рёбер CD и CC’ соответственно. Найдите расстояние между прямыми AN и BM.

13. В основании прямой треугольной призмы лежит правильный треугольник АВС со стороной 1, её боковые рёбра равны 2. Точки К и L – середины рёбер АВ и CC’ соответственно. Найдите расстояние между прямыми KL и A’C.

14. Пусть АВСА₁В₁С₁ – правильная призма с основанием АВС, боковыми рёбрами АА₁, ВВ₁, СС₁, причём все рёбра призмы равны 2. Пусть точка М – середина ребра СС₁. Найдите минимальный возможный радиус сферы, касающейся прямых А₁С и ВМ.

15. Дан параллелепипед ABCDA’B’C’D’, АС и DC’- диагонали его граней. Докажите, что существует пара точек таких, что и найти отношение .

16. В параллелепипеде через середину ребра ВС проведена прямая, пересекающая прямые AC’ и DD’ соответственно в точках N и Р. Найдите отношение .

17. Даны точки М и N – середины ребер АВ и DC тетраэдра ABCD, точка Р принадлежит ребру AD так, что . В каком отношении плоскость MNP делит ребро ВС?

18. Дана четырехугольная пирамида PABCD с вершиной Р, в основании – параллелограмм ABCD. На ребрах РА и РС взяты точки К и М соответственно так, что . Найдите отношение, в котором до так, что . Найдите отношение, в котором делится ребро РВ плоскостью DKM.

19. Точки М и N – соответственно середины рёбер АС и SB правильного тетраэдра SABC. Рёбра тетраэдра равны 1. На прямых AS и CN выбраны точки Р и Q так, что прямая PQ параллельна прямой ВМ. Найдите длину отрезка PQ.

20. Дан куб ABCDA’B’C’D’ с основанием ABCD и боковыми рёбрами AA’, BB’, CC’, DD’. Точка N – середина ребра АВ; точка М – середина ребра BB’, точка О – точка пересечения диагоналей грани BCC’B’. Через точку О проведена прямая, пересекающая прямые АМ и CN в точках Р и Q соответственно. Найдите длину отрезка PQ, если длина ребра куба равна 1.

21. Ребро куба ABCDA’B’C’D’ равно 2а. Отрезок PQ, концы которого лежат на прямых BC’ и AB’, пересекается с прямой CD’ в точке О и делится этой точкой пополам. Найдите длину отрезка PQ.