Пример синтеза генератора кодов

 

Требуется синтезировать генератор двоичных кодов, заданных числовой последовательностью: 4-1-2-6-7-5-0-3.

Дополнительная переменная Y равна единице, если формируемые числа равны 5, 6 или 7.

Длина формируемой последовательности - восемь тактов, диапазон изменения чисел от 0 до 7, значит, для обеспечения требуемого числа внутренних состояний (всех кодовых комбинаций) потребуются три триггера, и основные сигналы можно получить с выходов этих триггеров без комбинационной схемы, формируя комбинационно только дополнительный сигнал Y. Поставив в соответствие формируемым числам коды внутренних состояний КА Q3Q2Q1, получим граф переходов (см. рис.5.1):

 
 

 

 


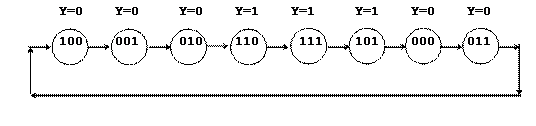Рис.5.1.


 

Временная диаграмма работы синтезируемого генератора приведена на рис.5.2.

 

 

 

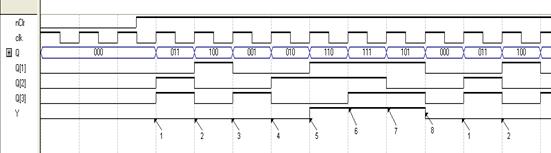
Рис.5.2.

 

На основании графа переходов строим таблицу переходов синтезируемого КА

rt
rt+1

Используя для реализации КА JK-триггеры с функцией возбуждения (см. п.4.2):

  Q(t)®Q(t+1)
Входы 0®0 0®1 1®0 1®1
J H H
K H H

 

построим таблицу возбуждения КА и дополним её таблицей истинности функции Y:

 

Значение кода Q3Q2Q1 J3K3 J2K2 J1K1 Y
0 0 0 0 H 1 H 1 H
0 0 1 0 H 1 H H 1
0 1 0 1 H H 0 0 H
0 1 1 1 H H 1 H 1
1 0 0 H 1 0 H 1 H
1 0 1 H 1 0 H H 1
1 1 0 H 0 H 0 1 H
1 1 1 H 0 H 1 H 0

 

Ориентируясь на использование JKFF-триггера, осуществим минимизацию полученных функций:

 

  Q2Q1     Q2Q1
Q3   Q3
1   H H H H
H H H H  

J3=Q2 K3= 2

  Q2Q1     Q2Q1
Q3   Q3 01
0 H H   H H
H H   H H

J2= 3 K2= Q1

 

  Q2Q1     Q2Q1
Q3 00   Q3 00
H H   H H
1 H H   H H

J1= 2+Q3 K1= 2+ 3

  Q2Q1
Q3
0

 

Y =Q3Q1+Q3Q2

 

 
 


J3=K3=Q2; J2= 3; K2= 1; J1=Q2 3; K1=Q2Q3;

 

 

Y= Q3Q1 × Q3Q2

Запишем логические выражения в базисе Шеффера:

 

Отметим возможность совместной реализации функций K1 и Y.

Используя триггеры и ЛЭ из состава библиотеки примитивов, составим принципиальную схему реализации генератора, приведенную на рис.5.3.

 

 

Рис.5.3.