ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

1. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при среднем квадратическом отклонении 700 ч. При 5-% уровне значимости проверить гипотезу о том, что значение 2900 ч является математическим ожиданием.

 

2. Составлена выборка из 64 покупателей, которые интересовались товаром А. Из них товар А купили 16 человек. Поставщик утверждает, что данный товар должен привлечь треть покупателей, а среднее квадратическое отклонение равно одному человеку. Проверить нулевую гипотезу при 5-% уровне значимости.

 

3. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при выборочном среднем квадратическом отклонении 0,1 мм. При 5-% уровне значимости проверить гипотезу о том, что станок, на котором изготавливают подшипники, не требует подналадки.

 

4. По результатам 10 замеров установлено, что среднее время обслуживания мастером клиента равно 15 мин. Предполагая, что время обслуживания – нормально распределенная случайная величина, с дисперсией 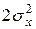=9 при уровне значимости 0,05 установить, можно ли принять в качестве норматива для обслуживания одного клиента 21 мин?

 

5. Из большой партии ананасов одного размера извлечена выборка из 36 штук. Выборочная средняя масса одной штуки при этом оказалось равна 930 г. Используя двусторонний критерий проверить гипотезу о том, что средняя масса одного ананаса составляет 1 кг., если:

А) среднее квадратическое отклонение известно и составляет 200 г.;

Б) среднее квадратическое отклонениенеизвестно, а выборочное составляет 250 г.

 

6. На двух станках производят одну и туже продукцию, контролируемую по наружному диаметру изделия. Из продукции станка А было проверено 16 изделий, а из продукции станка В – 25 изделий. Выборочные оценки математических ожиданий и дисперсий контролируемых размеров составили 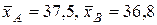, s_A²=1,21, s_B²=1,44. Проверить гипотезу о равенстве дисперсий при α=0.1.

 

7. Точность работы станка проверяется по дисперсии контролируемого размера изделий, которая не должна превышать 0,1. Взята проба из 25 случайно отобранных изделий, причем получено, что выборочная дисперсия контролируемого размера равна 0.2. Требуется при уровне значимости 0,05 проверить, обеспечивает ли станок необходимую точность.

 

8. Средний ежедневный объем продаж за I квартал текущего года для 17 торговцев района А составляет 15 тыс. руб при исправленном среднем квадратическом отклонении 2,5 тыс.руб, а для 10 торговцев района В – 13 тыс.руб при исправленном среднем квадратическом отклонении 3 тыс.руб. Существенно ли различие объемов продаж при 5%-муровне значимости для районов А и В?

 

9. Фирма продает автоматы по розливу напитков. По выборке из n=16 средняя величина дозы, наливаемой в стакан первым автоматом – 182 г.По выборке m=9 средняя величина величина дозы, наливаемой в стакан вторым автоматом – 185 г. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальное распределение с дисперсией 25 г. Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости 0,01?

 

10. Четыре исследователя параллельно определяют процентное содержание углерода в сплаве, причем первый исследователь произвел анализ 25 проб, второй 33, третий – 29, четвертый – 33 проб. Исправленные выборочные средние квадратические отклонения оказались соответственно равными 0,05; 0,07; 0,10; 0,08. Требуется при уровне значимости 0,01 проверить гипотезу об однородности дисперсий в предположении, что процентное содержание углерода в сплаве распределено нормально.

 

11. 4 фасовочных автомата настроены на отвешивание одного и того же веса . На каждом автомате отвесили по 10 проб, а затем эти же пробы взвесили на точных весах и нашли по полученным отклонениям исправленные дисперсии: 0,012; 0,021; 0,025; 0,032. Можно ли при уровне значимости 0,05 считать, что автоматы обеспечивают одинаковую точность взвешивания?

 

12. В течение 64 дней в фирму А обращалось 87 человек в день, а в фирму В – 93 человека в день. Есть ли основание утверждать нга уровне значимости 5%, что фирма В более популярна, чем А , если дисперсия числа клиентов в день для А – 124, для В – 132?

 

13. Аудиторы компании интересуются системой обработки счетов доходов. Они взяли случайную выборку объема 50, в ней оказалось 4 счета с дефектами. Аудиторы предложили модификации обработки счетов. Через определенное время взяли выборку из 60 счетов. В ней оказалось 3 с дефектами. Имеется ли основание утверждать при 5% уровне значимости, что новые процедуры уменьшают ошибку?

 

14. Партия принимается, если вероятность того, что изделие бракованное, не превышает 0,02. Среди случайно отобранных 480 изделий оказалось 12 дефектных. Можно ли при 5% уровне значимости принять партию?

 

15. Партия принимается, если вероятность того, что изделие бракованное, не превышает 0,03. Среди случайно отобранных 400 изделий оказалось 18 дефектных. Можно ли при 5% уровне значимости принять партию?