Тема 3. Эксплуатация скважин штанговыми насосами
Две трети фонда (66%) действующих скважин стран СНГ эксплуатируются штанговыми скважинными насосными установками (ШСНУ). Дебит скважин составляет от нескольких десятков килограммов в сутки до нескольких тонн. Насосы спускают на глубину от нескольких десятков метров до 3000 м. ШСНУ включает в себя следующие элементы:
1) наземное оборудование: станок-качалка, оборудование устья;
2) подземное оборудование: насосно-компрессорные трубы, насосные штанги, штанговый скважинный насос и различные защитные устройства, улучшающие работу устройства в осложненных условиях [9].
Отличительная особенность ШСНУ состоит в том, что в скважине устанавливается плунжерный насос, который приводится в действие поверхностным приводом посредством колонны штанг.
Нагрузки, действующие при работе глубинного насоса в точке подвеса насосных штанг (на полированный шток), состоят из следующих элементов:
1) статических нагрузок от веса насосных штанг и жидкости, а также сил трения плунжера в цилиндре насоса и трения насосных штанг о трубы;
2) динамических нагрузок, вызываемых силами инерции движущихся масс насосных штанг и жидкости, а также вибрацией штанг [5, 7, 9].
Нагрузки на штанги, возникающие от указанных причин, действуют одновременно, и для практических целей необходимо знать их совокупное действие. Но ввиду сложности определения динамических нагрузок расчетным путем наиболее точным и простым способом их учета является непосредственное измерение этих нагрузок при помощи динамографа.
Задача
По динамограмме нормальной работы штангового скважинного насоса (см. рисунок 8) определить максимальную и минимальную нагрузки на полированный шток, амплитуду колебаний нагрузки, максимальное напряжение в верхней штанге и коэффициент подачи насосной установки, если масштаб усилий динамографа составляет 80 Н на одно деление, а масштаб хода равен 1:30.
Максимальное усилие будет возникать в т. М, а минимальное – в т. А
;
.
Амплитуда колебаний нагрузки за один цикл (ход вверх и вниз)
Максимальное напряжение в верхней штанге
, (3.1)
где fш – площадь поперечного сечения штанги.
Рисунок 8 – Динамограмма работы глубинного насоса
Потеря хода плунжера bВ вследствие деформации насосных штанг и труб
λ = (28 - 18)·30 = 300 мм.
Коэффициент подачи насосной установки, учитывающий наполнение насоса и упругие удлинения штанг и труб, равен
m = ВС / Аd = (115-28) / (115-18) = 0,90.
Однако, как бы ни сложны были динамические нагрузки, их необходимо учитывать при проектировании нового оборудования ШСНУ. Для расчета усилий, действующих в колонне штанг, а также в элементах привода имеют значения прежде всего максимальное и минимальное усилия, действующие в течение двойного хода штанг. Указанные усилия были определены А.С. Вирновским, который вывел формулы, позволяющие с достаточной степенью точности описывать нагружение штанг. В настоящее время их используют как эталонные при проверке результатов, получаемых с помощью других формул. Вместе с тем эти формулы достаточно сложны, и многие исследователи предлагали более простые зависимости. Например, А.Н. Адонин на основе большого количества экспериментальных данных предложил свои эмпирические зависимости, которые также нашли применение в инженерных расчетах [6, 7].
Задача
Определить максимальную нагрузку на головку балансира по формулам А.С. Вирновского и А.Н. Адонина и сравнить полученные результаты. Данные для расчета: глубина подвески вставного насоса L, диаметр плунжера насоса Dпл, диаметр насосных труб dт, колонна штанг двухступенчатая – длина штанг верхней ступени dш1 составляет 32%, длина нижней ступени dш2 равна 68%. Длина хода полированного штока S, число качаний в минуту n, плотность жидкости rж = 895 кг/м3.
Максимальная нагрузка на головку балансира может быть определена по различным формулам в зависимости от режима откачки жидкости.
По статической теории расчета учитываются только статические усилия (вес штанг и жидкости) и максимальное значение сил инерции. По исследованиям А.Н. Адонина, граница между статическим и динамическим режимами при откачке жидкости с больших глубин находится в зоне значений параметра m = (w×L)/а = 0,35 ¸ 0,45, где w - угловая скорость вращения кривошипов в радианах; а – скорость распространения звука в металле штанг, м/с. В настоящее время применяются в основном режимы при m < 0,5.
Указанные значения m отграничивают большую область статического режима работы штанговых насосов на глубинах до 1000 – 1200 м, а так же тихоходную работу на больших глубинах. За пределами этой области, т.е. при значительном увеличении глубины и скорости откачки, следует применять динамическую теорию расчета [6, 7].
Максимальную нагрузку по элементарной (статической) теории определяли согласно [6, с.275] по формуле
, (3.2)
, (3.3)
, (3.4)
где Рж – вес столба жидкости над плунжером, высотой равной глубине
установки насоса L (предусматривается наиболее тяжелый случай,
когда динамический уровень находится у приема насоса);
Рш – полный вес насосных штанг;
в – коэффициент потери веса штанг в жидкости;
m – фактор динамичности;
ρш , ρж – соответственно плотность материала штанг и жидкости;
S – длина хода полированного штока;
N – число качаний в мин.
, (3.5)
где Fпл – площадь плунжера;
L – глубина установки насоса.
Максимальную нагрузку на основе динамической теории по формуле А.С.Вирновского с учетом собственных колебаний колонны штанг определяли согласно [6, с.276] по формуле:
, (3.6)
где Рж – вес столба жидкости между плунжером и штангами:
, (3.7)
S – длина хода точки подвеса штанг (ТПШ);
w – угловая скорость вращения кривошипа;
, (3.8) 
ε – отношение площадей просвета,
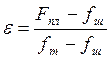, (3.9)
fт – площадь проходного сечения трубы НКТ;
α1иа1 – коэффициенты, зависящие от кинематики станка качалки;
α1 – коэффициент, равный отношению угла поворота кривошипа 
к
углу его поворота, при котором скорость достигает максимума;
а1 – кинематический коэффициент
, (3.10)
r – радиус кривошипа;
S – длина хода ТПШ;
Ψ – коэффициент
, (3.11)
f'т – площадь сечения труб по металлу;
λшт – удлинение штанг от веса столба жидкости
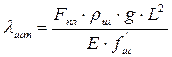, (3.12)
ρш – плотность материала штанг;
Е – модуль упругости материала штанг
Е = 2,1·105 МПа.
f'''ш – средняя площадь поперечного сечения штанг.
Максимальную нагрузку на основе динамической теории А.Н.Адонина определяли согласно [6, с.277] по формуле:
; (3.13)
, (3.14)
где ε – отношение площадей просвета;
т – кинематический коэффициент;
r – радиус кривошипа;
lш – длина шатуна.
Варианты заданий к пятой контрольной задаче по теме «Определение нагрузок штанговой колонны»
| № варианта | L, м | Dпл, мм | d  , мм
| dш1, мм | dш2, мм | Тип станка-качалки | S, м | n | Радиус кривошипа r, мм | Длина шатуна l, мм |
| СК2-0,6-250 | 0,6 | |||||||||
| СК2-0,6-250 | 1,6 | |||||||||
| СК2-0,6-250 | 0,6 | |||||||||
| СК2-0,6-250 | 2,4 | |||||||||
| СК2-0,6-250 | 0,6 | |||||||||
| СК2-0,6-250 | 1,8 | |||||||||
| СК3-1,2-630 | 0,6 | |||||||||
| СК3-1,2-630 | 0,75 | |||||||||
| СК3-1,2-630 | 0,9 | |||||||||
| СК3-1,2-630 | 1,2 | |||||||||
| СК3-1,2-630 | 1,05 | |||||||||
| СК4-2,1-1600 | 0,9 | |||||||||
| СК4-2,1-1600 | 1,2 | |||||||||
| СК4-2,1-1600 | 1,5 | |||||||||
| СК4-2,1-1600 | 1,8 | |||||||||
| СК4-2,1-1600 | 2,1 | |||||||||
| СК4-2,1-1600 | 1,3 | |||||||||
| СК5-3-2500 | 1,3 | |||||||||
| СК5-3-2500 | 1,8 | |||||||||
| СК5-3-2500 | 2,1 | |||||||||
| СК5-3-2500 | 2,5 | |||||||||
| СК5-3-2500 | ||||||||||
| СК5-3-2500 | 2,8 | |||||||||
| СК5-3-2500 | 0,9 | |||||||||
| СК5-3-2500 | 1,6 | |||||||||
| СК6-2,1-2500 | 0,9 | |||||||||
| СК6-2,1-2500 | 1,2 | |||||||||
| СК6-2,1-2500 | 1,5 | |||||||||
| СК6-2,1-2500 | 1,8 | |||||||||
| <1-2500 | 1,8 | |||||||||
| СК6-2,1-2500 | 2,1 | |||||||||
| СК6-2,1-2500 | 1,1 | |||||||||
| СК8-3,5-4000 | 1,8 | |||||||||
| СК8-3,5-4000 | 2,1 | |||||||||
| СК8-3,5-4000 | 2,5 | |||||||||
| СК8-3,5-4000 | 3,0 | |||||||||
| СК8-3,5-4000 | 3,5 | |||||||||
| СК8-3,5-4000 | 2,3 | |||||||||
| СК5-3-2500 | 2,0 | |||||||||
| СК3-1,2-630 | 1,2 | |||||||||
| СК2-0,6-250 | 1,6 |
return false">ссылка скрыта