Алгебраические линии и поверхности
Пусть на плоскости задана некоторая аффинная система координат. Тогда любая точка плоскости задается парой  действительных чисел.
действительных чисел.
Определение 1. Множество точек плоскости, координаты которых в некоторой системе координат удовлетворяют уравнению
 (1)
(1)
называется линией. Если уравнение (1) разрешимо относительно y, то оно переписывается
 . (1’)
. (1’)
Иногда для описания линии используют векторную форму записи:
 . (2)
. (2)
Здесь параметр  ,
,  - радиус-вектор точек на линии, при изменении t концы
- радиус-вектор точек на линии, при изменении t концы  описывают некоторую линию.
описывают некоторую линию.
Если на плоскости рассматривается декартова система координат, то каждый радиус-вектор  может быть представлен
может быть представлен  . Тогда уравнение (2) в координатах принимает вид
. Тогда уравнение (2) в координатах принимает вид
 (3)
(3)
- параметрическое уравнение линии.
Например, 
 - уравнение окружности, а
- уравнение окружности, а
 - уравнение спирали (см. рис.).
- уравнение спирали (см. рис.).

Линию на плоскости иначе можно задать в полярной системе координат уравнением следующего вида:
 ,
,
где 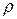 - длина
- длина  ,
,  - полярный угол.
- полярный угол.
Например,  - полярное уравнение линии.
- полярное уравнение линии.
Если перечисленные уравнения рассматривать парами, т.е.
 или
или  или
или  или
или 
Тогда каждая система определяет множество точек, являющихся пересечением двух линий.
Аналогично, множество решений уравнения
 , (5)
, (5)
можно рассматривать как поверхность в трехмерном пространстве, где  - координаты точки в заданной системе координат. Если (5) разрешимо относительно одной из переменных, то оно может быть, например, переписано в виде
- координаты точки в заданной системе координат. Если (5) разрешимо относительно одной из переменных, то оно может быть, например, переписано в виде
 . (5’)
. (5’)
Замечание. Если уравнение поверхности (5) не содержит одной из переменных, то соответствующая поверхность называется цилиндрической.
Прямые линии, из которых она состоит, называются её образующими, а линию, лежащую на поверхности и пересекающую все образующие, называют направляющей.
Пример. Образующие и направляющая для поверхности  (параболический цилиндр) приведены на рисунке.
(параболический цилиндр) приведены на рисунке.

Если рассматривать систему
 , (6)
, (6)
состоящую из двух уравнений поверхностей, то система (6) в общем случае описывает кривую пересечения этих поверхностей.
Пример. Множество всех решений системы

представляет собой окружность радиуса  , расположенную на высоте 1/2 от плоскости Oxy.
, расположенную на высоте 1/2 от плоскости Oxy.
Любую кривую в пространстве можно также описать в виде
 (7)
(7)
- векторное параметрическое уравнение линии.
Если  , то уравнение (7) в координатах принимает вид
, то уравнение (7) в координатах принимает вид
 (8)
(8)
- координатное параметрическое уравнение линии в пространстве.
Определение 2. Алгебраической поверхностью называется множество точек, которые в какой-либо аффинной системе координат удовлетворяют уравнению:
 (9)
(9)
где  . Величина наибольшей из сумм
. Величина наибольшей из сумм  называется порядком алгебраической поверхности.
называется порядком алгебраической поверхности.
Аналогичное определение вводится для алгебраической линии на плоскости.
Теорема 1. Алгебраическая поверхность порядка p в любой аффинной системе координат может быть задана уравнением вида (9) порядка p.
Доказательство. Пусть в некоторой аффинной системе координат поверхность задана уравнением (9). Тогда при переходе в другую аффинную систему координат переменные  преобразуются по формулам:
преобразуются по формулам:
 (10)
(10)
где  - матрица перехода к другому базису, а вектор
- матрица перехода к другому базису, а вектор  - координаты преобразованного начала координат. Очевидно, что после подстановки (10) в (9) порядок уравнений не повышается.
- координаты преобразованного начала координат. Очевидно, что после подстановки (10) в (9) порядок уравнений не повышается.
Если бы после подстановки (10) в (9) порядок полученного уравнения повысился, то в силу обратимости (10) порядок поверхности мог бы возрасти, а это невозможно. Таким образом, при переходе к другой системе координат порядок поверхности не изменяется, ч.т.д.∎