Тензорные поля в криволинейных координатах.

Рассмотрим систему криволинейных координат 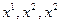. Радиус-вектор 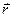точки является функцией её координат: .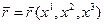

В тензорном анализе за векторы локального базиса в данной точке принимаются векторы, равные частным производным 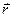по координатам:

.

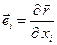При преобразовании координат 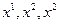преобразуются векторы локального базиса: если 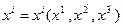, то 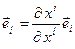, так как .

Векторы 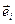направлены по касательным к координатным линиям в сторону возрастания координаты и в общем случае отличны по модулю от 1. В физике за векторы локального базиса принимаются единичные векторы, сонаправленные :

.

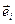Координаты вектора 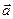относительно базиса 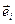обозначаются 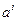, а относительно базиса 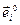обозначаются :

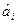Следовательно, 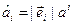; ; 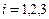не суммировать. Числа 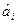называются физическими компонентами вектора .

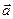Векторы 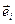являются функциями координат точки: .

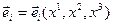Координаты векторных и тензорных полей также представляют собой функции точки.

Координаты метрического тензора выражаются через векторы локального базиса:

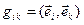
Выражение для дифференциала радиуса вектора имеет вид

.

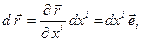Зная метрический тензор, можно найти квадрат дифференциала длины дуги:

.

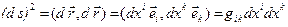Таким образом, .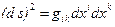

Наоборот, зная выражение для 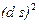, можно найти координаты метрического тензора, как коэффициенты этого выражения.

Если система координат ортогональная, то 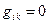при 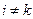, и выражение для 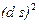имеет вид

.

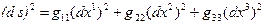Пример. Найти квадрат дифференциала длины дуги и метрический тензор для сферической системы координат .

Решение. .

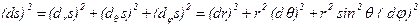
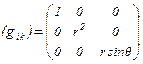
Зависимость между контравариантными и ковариантными координатами вектора выражается формулой 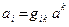; для ортогональной системы координат эта зависимость имеет вид

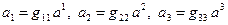или .

Переход к физическим компонентам вектора производится по формулам ,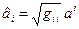
так как .

Полезно найти также элемент объёма в криволинейных координатах:

.

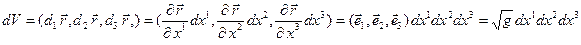Таким образом, 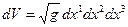, где .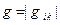

Например, в сферических координатах

.

 

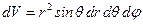Пример. Дано скалярное поле . Найти .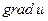

Решение.

. Здесь 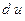– инвариант, 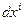– контравариантный вектор (вектор ).

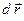Следовательно, по признаку тензора, – ковариантный вектор, т.е. 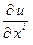– ковариантные координаты вектора. Обозначим его . Тогда . Этот вектор не зависит от системы координат. В частном случае, когда система координат декартова, координаты 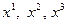переходят в декартовы координаты 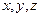, а векторы в орты координатных осей .

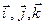Следовательно, .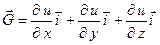

Таким образом, в любой системе координат справедливо следующее выражение для :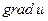

.

Координаты взаимного базиса 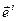выражаются через 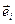по формулам .

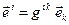Следовательно, .

 

Если базис ортогональный, то 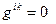при 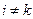, Выражение для градиента принимает вид 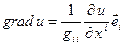. Для того, чтобы перейти к физическим компонентам, нужно подставить формулу выражения 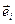через 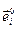. Выражение для 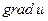примет вид

Например, в сферических координатах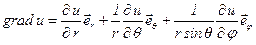

Если система криволинейных координат ортогональная, то используются обозначения

;

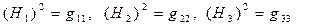называются коэффициентами (параметрами) Ламе.

В этих обозначениях ( для ортогональной системы координат):

Например, для сферических координат 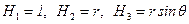.