Th 2. Критерий разложимости функции в степенной ряд
Пусть функция  бесконечно дифференцируема в точке
бесконечно дифференцируема в точке  . Для того, чтобы функция
. Для того, чтобы функция  в промежутке
в промежутке  разлагалась в ряд Тейлора с центром
разлагалась в ряд Тейлора с центром  необходимо и достаточно, чтобы остаточный член в формуле Тейлора (9) во всех точках
необходимо и достаточно, чтобы остаточный член в формуле Тейлора (9) во всех точках  стремился к нулю при
стремился к нулю при  .
.
□
Раз у функции имеются производные всех порядков, то имеет место формула
 .
.
 - остаточный член формулы Тейлора.
- остаточный член формулы Тейлора.
Если  , то
, то  . И наоборот, если ряд сходится, то
. И наоборот, если ряд сходится, то  и
и  .
.
■
Разложение в ряд Маклорена элементарных функций.
1.  . (13)
. (13)
Найдем радиус сходимости этого ряда


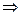 ряд (13) сходится на промежутке
ряд (13) сходится на промежутке  .
.
2. 
 . (14)
. (14)
Ряд (14) сходится на промежутке  .
.
Аналогично можно получить:
3.  ,
,  . (15)
. (15)
4.  ,
,  . (16)
. (16)
5.  ,
,  . (17)
. (17)
6.  , если
, если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то  . (18)
. (18)