Поперечный уклон. Определение и оценка.

Под поперечным уклоном понимается отклонение поверхности элемента дорожной конструкции (земляного полотна, слоев дорожной одежды) от горизонтального уровня, измеряемое в направлении перпендикулярном к оси дороги. Поперечный уклон дороги влияет на устойчивость, управляемость автомобиля и используется в расчетах эксперта при определении критических параметров движения автомобиля на уклоне.

Поперечный уклон (i_поп) измеряют и вычисляют аналогично продольному (см. п. 4.4). На виражах поперечный уклон измеряют на всем протяжении кривой перпендикулярно к осевой линии проезжей части. Принимают i_поп со знаком «+», если плоскость дороги наклонена к центру поворота, и i_поп со знаком «-», если плоскость дороги наклонена от центра поворота.

Нормативные значения поперечного уклона приведены (в промилле) ниже в зависимости от типа покрытия (на горизонтальном участке), а в табл.4.5.1 приложения 6 (на виражах) - в зависимости от значения радиуса кривых в плане:

Асфальто- и цементобетонные ………………………. 15-20

Брусчатая и клинкерная мостовая …………………… 20 - 25

Покрытие из щебня (гравия) и других материалов, обработанных органическими вяжущими веществами ……………… 20 - 25

Щебеночное (гравийное)………………………………. 25 - 30

Мостовая из булыжного и колотого камня …………... 30 - 40

Грунтовое, укрепленное местными материалами …..... 30 - 40

4.6. Радиус кривой дороги в плане.

Кривая в плане - один из основных элементов автомобильной дороги, которая представляет собой криволинейный участок, сооружаемый при изменении направления трассы.

Наименьший (нормативный) радиус кривой дороги в плане - радиус, при котором обеспечивается безопасное движение автомобилей с расчетной скоростью на чистом увлажненном и уширенном покрытии, имеющем нормативный вираж проезжей части.

Величина радиуса закругления дороги по его протяженности, как правило, не одинакова. Средняя часть кривой имеет наименьший, но постоянный радиус закругления и называется круговой кривой. На сопряжении круговой кривой с прямым участком дороги, которое называется переходной кривой, кривизна закругления плавно изменяется. Тем самым обеспечивается плавное нарастание центробежной силы при входе в поворот, которая оказывает существенное влияние на условия и удобства движения ТС в пределах закругления дороги (рис. 4.6.1).

Радиус кривой дороги в плане влияет в основном на устойчивость и управляемость автомобиля и используется в расчетах эксперта при определении критических параметров движения автомобиля на повороте.

 

4.6.1. Определение постоянного радиуса кривой в плане.

Если необходимо замерить величину радиуса кривой в плане на участках с постоянным радиусом или на небольшом участке переходной кривой, то можно воспользоваться одним из описанных ниже способов.

Наиболее простой способ определения радиуса на месте ДТП в пределах обследуемой зоны заключается в измерении длины хорды L (между двумя точками, находящимися на кромке проезжей части) и высоты сегмента f (перпендикуляра, восстанов­ленного из середины хорда L до пересечения с кромкой проезжей части). Измерив с точностью до 0,1м указанные на рис. 4.6.2 величины L и f,можно вычислить фактический радиус R по формуле

R = ,

где f - высота сегмента;

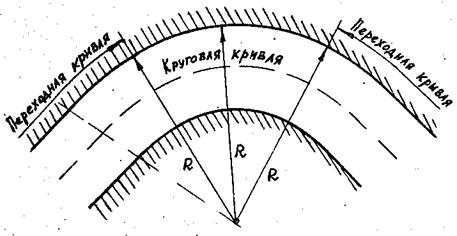Рис. 4.6.1. Общий вид кривой в плане. Рис.4.6.2. Измерение кривой с помощью мерных лент.

L - длина хорды.

Для упрощения в полевых условиях можно воспользоваться заранее приготовленным приспособлением, которое состоит из двух мерных лент различной длины: 20м и 1,5м. К середине 20-метровой ленты (в отметке 10м) крепится полутораметровая лента. Натягивая 20-метровую мерную ленту между двумя точками на кривой, измеряем высоту сегмента по полутораметровой ленте, которая также натягивается. Для удобства в работе можно использовать табл. 4.6.1, которая составлена на основе заранее проведенных расчетов (для ленты длиной L = 20м).

 

Таблица 4.6.1.

Определение радиусаR кривой по высоте f сегмента, м

f	1,01	0,67	0,5	0,4	0,33	0,25	0,2	0,17	0,12	0,1	0,08	0,07	0,06	0,05
R

Примечание. Перед проведением замеров фиксируют по всей длине участка, на котором проводятся измерения, внутреннюю и внешнюю кромки проезжей части. Если замеры необходимо провести по оси кривой, размечают середину проезжей части и проводят осевую.

Для измерения методом Н.А. Володина и Я.И. Середняка, уточненным и доработанным сотрудниками кафедры «Автомобильные дороги» КПП им. С. Лазо, пользуются теодолитом Т-30 (или другим, имеющим цену деления 1) с нивелировкой, трехметровой рейкой, мерной 50-метровой лентой или 100-метровым тросом.

Для определения радиуса круговой кривой инструмент устанавливают в районе предполагаемой середины кривой (например, в точке А, рис. 4.6.3). В продольной точке вдоль кромки проезжей части устанавливают рейку и определяют расстояние АВ. Откладывая в другую сторону от инструмента расстояние АВ вдоль кромки проезжей части, получают точку С. Измеренный угол между направлениями АВ и АС и является внутренним углом закругления.

Рис. 4.6.3. Схема инструментального определения радиуса кривой.

Имея значения угла α и расстояния АВ = АС = d, определяют радиус кривой по формуле

R = .

Для исключения расчетов в полевых условиях составлены специальные таблицы. В одной при известном расстоянии d = 50м, даны значения радиусов кривых от 50 до 100м, в другой - при d = 100м для различных углов α даны значения радиусов кривых в плане от 100 до 1200м.