Определение выигрышей в игре без седловых точек

Средний выигрыш игрока А в том случае, когда оба игрока применяют свои оптимальные смешанные стратегии (функция выигрыша игрока А в смешанных стратегиях) равен

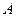где вектор-строка задает вероятности применения различных чистых стратегий первым игроком , - платежная матрица и - вектор-столбец вероятностей применения чистых стратегий вторым игроком:

В тех случаях, когда один из игроков применяет чистую стратегию, а второй – смешанную, нужно “занулить” все вероятности, соответствующие неиспользуемым этим игроком стратегиям. Например, если первый игрок использует чистую стратегию , то для определения выигрыша достаточно заменить вектор на вектор .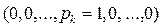

 

Пример 3. Задана платежная матрица

		1/2	5/6
		3/4	1/2

 

Пусть оптимальные смешанные стратегии игроков А и В уже определены:

 

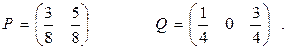
Требуется определить выигрыши игрока А в ситуациях, когда

 

1) игрок В применяет смешанную стратегию;

2) игрок В применяет одну из чистых стратегий ( , , или ).

 

 

Расчет выигрышей проведите, используя операцию произведения матриц (в данной форме результаты заносятся в ячейки D6, D14, D21 и D28). Проанализируйте полученные результаты.