Табличный процессор MS Excel. Условное форматирование
Задача 1. (10 баллов) Штатное расписание
1. На одном листе рабочей книги составить таблицу штатного расписания некой организации в соответствии с приведенным рисунком 1.
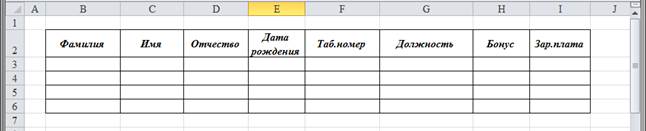
Рис.1
2. На втором листе составить таблицу вычисления заработной платы в соответствии с рисунком 2.
В данной таблице столбец "Итого" заполняется как сумма полей "Оклад", "Доплата 1" и "Доплата 2". Столбец "Бонус" необходим для начисления заработной платы.
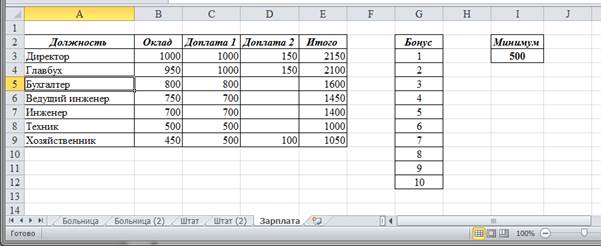
Рис.2
3. Заполнить таблицу рис.1 исходными данными, которых должно быть не менее 20. При этом учесть, что заработная плата начисляется в зависимости от должности (поле "Итого" таблица рис.2 ) и суммы "Бонуса", умноженного на заданный "Минимум" (=ИНДЕКС(Зарплата!$E$3:$E$9;ПОИСКПОЗ(Штат!G3;Зарплата!$A$3:$A$9;0))+Зарплата!$I$3*ПРОСМОТР(Штат!H3;Зарплата!$G$3:$G$12) )
4. Скопировать исходную таблицу (рис.1). Провести фильтрацию данных:
А) Список сотрудников по заданной должности
Б) Список однофамильцев (если нет данных в таблице, то добавить их_
В) Список сотрудников, старше заданного возраста
Г) Список сотрудников, получающих заработную плату в интервале от 3500 руб. до 7200 руб.
5. Скопировать исходную таблицу (рис.1). Провести сортировку данных:
А) Алфавитный порядок по фамилии
Б) Обратный хронологический порядок по возрасту
6. Скопировать исходную таблицу. Провести условное форматирование ячеек по заданному критерию:
А) Выделить синим цветом ячейки, содержащие заработную плату менее 2000 руб., зеленым цветом – более 2000 руб., но мене 6000, красным цветом – более 6000 руб.
Например, таблица может выглядеть так:
Рис.3
Задача 2.. (10 баллов) Задача о рациональном питании
Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно С1, С2, С3, С4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков – не менее b1 единиц; углеводов – не менее b2 единиц; жиров – не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где aij (i=1,2,3,4; j=1,2,3) – какие–то определённые числа; первый индекс указывает номер продукта, второй – номер элемента (белки, углеводы, жиры). |продукт | элементы || |белки |углеводы |жиры ||П1 |A11 |A12 |A13 ||П2 |A21 |A22 |A23 ||П3 |A31 |A32 |A33 ||П4 |A41 |A42 |A43 |Требуется составить такой пищевой рацион (т.е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.МАТЕМАТИЧЕСКАЯ МОДЕЛЬ. Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, - стоимость рациона (обозначим её L): она линейно зависит от элементов решения x1, x2, x3, x4. Целевая функция:
Система ограничений: a11x1+a21x2+a31x3+a41x4=b1 a12x1+a22x2+a32x3+a42x4=b2 a13x1+a23x2+a32x3+a43x4=b3Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4.Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных x1, x2, x3, x4, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
Требуется спроектировать решение задачи в табличном процессоре Excel, на примере конкретных продуктов. Задача 3.. (5 баллов) Выпуск изделий
Предприятие выпускает 3 вида изделий. Для выпуска единицы изделия необходимо сырье в количестве 3 кг для 1-го вида, 8 кг для 2-го вида и 1 кг для 3-го вида. Общий запас сырья составляет 9500 кг. Изделия по видам входят в комплект в количестве 2, 1 и 5 штук соответственно. Определить оптимальное количество выпуска изделий, при котором количество комплектов будет максимальным. Комплекты немедленно отправляются потребителю. Склад вмещает не более 20 штук лишних изделий 2-го вида.
Задача 4. (5 баллов)Цирк
Рассчитайте еженедельную выручку цирка, если известно:
- количество проданных билетов каждый день
- цена взрослого билета - 15 руб.
Постройте диаграмму (график) ежедневной выручки цирка:
А) за неделю
Б) за месяц
В) за квартал. Найдите максимальную и минимальную выручку за квартал.
Для заполнения исходных данных можно воспользоваться функцией СЛЧИС(), которая определяет случайное число в диапазоне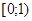 
. Чтобы найти случайное число на отрезке [a,b], надо спроектировать отрезок [0,1) на отрезок [a,b]. Для этого составляется формула:
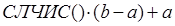
Задача 5.(5 баллов)Зоопарк
Рассчитайте еженедельную выручку зоопарка, если известно:
- количество проданных билетов каждый день
- цена взрослого билета - 15 руб.
- цена детского на 30% дешевле, чем взрослого.
Постройте диаграмму (график) ежедневной выручки зоопарка:
А) за неделю
Б) за месяц
В) за квартал, найдите максимальную и минимальную выручку за квартал.
Для заполнения исходных данных можно воспользоваться функцией СЛЧИС().
Задача 6.(5 баллов)
Подготовьте бланк заказа для магазина, если известно:
- продукты(хлеб, мука, макаронные изделия и т.д., не менее 10 наименований)
- цена каждого продукта
- количество заказанного каждого продукта
Рассчитайте на какую сумму заказано продуктов. Усовершенствуйте бланк заказа, добавив скидку (например 10%), если стоимость купленных продуктов будет более 5000 руб. Постройте диаграмму (гистограмму) стоимости заказанного товара.
Задача 7.(5 баллов)
Цена на хлеб составляет N руб. за булку хлеба. Прогнозируемая инфляция составляет 0,3% в месяц. Вычислите сколько средств (в руб.) тратит семья на покупку хлеба в год, если ежедневно семья покупает 2 булки хлеба. Построить диаграмму (график) зависимости цены хлеба по месяцам.
Задача 8.(5 баллов)
Цена 1 куб. метра леса в январе - N долларов. Прогнозируемая инфляция составляет 17% в год. Рассчитайте стоимость (в руб., при этом курс доллара m -рублей/$ ) 1 куб. метра в конце года (декабрь). Постройте диаграмму (график) цены 1 куб. метра (в руб.) по месяцам.