Раздел 2. Векторная алгебра на плоскости и в пространстве

2.1 Понятие о векторах и скалярах

Векторной величиной или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной или скаляром называется всякая величина, направлением не обладающая. Например, сила, действующая на материальную точку, есть вектор, так как она обладает направлением. Скорость также является вектором. Температура тела – это скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность – также скалярные величины.

Если отвлечься от направления векторной величины, то ее, как и скалярную величину, можно измерить, выбрав соответствующую масштабную единицу. Но число, полученное в результате измерения, характеризует скалярную величину полностью, а векторную – лишь частично.

Векторную величину полностью можно охарактеризовать направленным отрезком, предварительно задав линейный масштаб.

2.2 Вектор в геометрии

Вектором называется направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом (или одной буквой, , , ...). Длина отрезка АВ называется длиной, или модулем вектора и обозначается , .

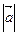Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают . Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) или противоположное.

Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 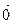или просто 0. По определению нулевой вектор не имеет направления и коллинеарен любому вектору.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через .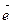

Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается 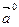. Два ненулевых вектора называются противоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору , обозначается ; вектор противоположен вектору ( ).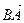

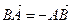Два коллинеарных вектора и называются равными ( ), если они сонаправлены и имеют равные длины.

Замечание. Нельзя смешивать понятия «равенство отрезков» и «равенство векторов». Говоря: «отрезки равны», мы утверждаем, что их можно совместить наложением. Но для этого один из них может быть придется подвергнуть повороту. Два вектора будут равны лишь в том случае, когда их можно совместить, не применяя поворот.

Совместим параллельным переносом начала неколлинеарных векторов и . Начало и концы векторов образуют вершины треугольника. Углом между векторами и называется угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°.

2.3 Векторная алгебра

Над векторами производят действия, называемые сложением, вычитанием и умножением векторов. Эти действия имеют много общих свойств с одноименными алгебраическими действиями. Поэтому учение о действиях над векторами называется векторной алгеброй.

Суммой двух векторов и называется вектор , соединяющий начало вектора с концом вектора , отложенного от конца вектора .

Обозначение: .

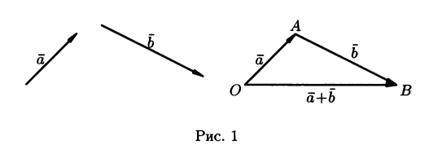
Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рис. 1 и 2 соответственно.

При сложении векторов имеют место неравенства:

1) ,

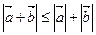2) ,

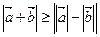выражающие, что сторона треугольника меньше суммы и больше разности двух других сторон (неравенство треугольника). В первой формуле равенство имеет место только для сонаправленных векторов, во второй – только для противоположно направленных векторов.

Сумма противоположных векторов равна нуль-вектору: .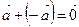

Суммой векторов 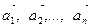называется вектор, получающийся после ряда последовательных сложений: к вектору прибавляется вектор , к полученному вектору прибавляется вектор и так далее.

Из определения вытекает следующее построение (правило многоугольника или правило цепи).

Из произвольного начала О откладываем вектор 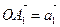, из точки А₁, как из начала, откладываем вектор , из точки А₂ строим вектор и так далее. Вектор 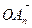есть сумма векторов .

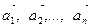Сложение векторов подчиняется коммутативному и ассоциативному свойствам:

1) ,

2) .

Коммутативность и ассоциативность сложения векторов позволяет нам находить сумму векторов в любом удобном порядке.

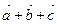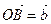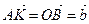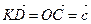Правило параллелепипеда. Если три вектора , и после приведения к общему началу не лежат в одной плоскости, то сумму можно найти следующим построением. Из общего начала О строим векторы , , . На отрезках ОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали равен сумме векторов , и , так как , , и .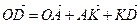

Под разностью векторов и понимается вектор такой, что 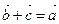. Обозначение: 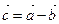. Справедливо равенство .

Произведением вектора на число 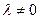называется вектор, который имеет длину 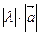, его направление если 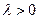и противоположное направление, если .

Обозначение: .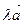

Отметим, что , т. е. каждый вектор равен произведению его модуля на орт.

Два ненулевых вектора и коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т. е. , λ – число (признак коллинеарности векторов).

Три ненулевых вектора , , компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например, (λ₁, λ₂ – числа не равные нулю одновременно) (признак компланарности векторов).

Умножение вектора на число подчиняется тем же законам, что и умножение чисел:

1. (дистрибутивный закон по отношению к числовому множителю).

2. (дистрибутивный закон по отношению к векторному множителю).

3. (ассоциативный закон).

Пример 1: В треугольнике ABC дано: 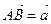, , 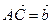точка М – середина стороны ВС. Выразить вектор через векторы и .

Решение:

Через точку М проведем прямые, параллельные сторонам АВ и АС. Получим параллелограмм АВ₁МС₁ (рис. 3), в котором AM является диагональю. Следовательно, . Но 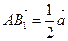, (B₁M и C₁M – средние линии, поэтому AB₁ = B₁B, AC₁ = С₁С). Получаем 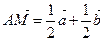, т.е. .

 

Пример 2: Какому условию должны удовлетворять ненулевые векторы и , чтобы имело место соотношение ?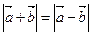

Решение:

Построим на векторах и , отложенных от точки О, параллелограмм OADB (рис. 4). Тогда , 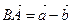. Равенство 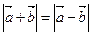означает, что длины диагоналей параллелограмма равны, т.е. 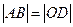. Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторы и перпендикулярны.

2.4 Скалярное произведение векторов

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла φ между ними (см. рис. 5). Обозначение: . Таким образом, .

По определению .

 

Свойства скалярного произведения:

1. (коммутативность);

2. (дистрибутивность);

3. (ассоциативность по отношению к скалярному множителю);

4. (скалярный квадрат вектора а равен квадрату его модуля);

5. (или , или ).

Векторы и , скалярное произведение которых равно нулю, называются ортогональными.

Пример 3 :Векторы и образуют угол . Зная, что и , вычислить .

Решение:

Согласно свойствам скалярного произведения .

Пример 4:Выразить длины медиан произвольного треугольника через длины его сторон.

Решение:

Рассмотрим треугольник АВС. Пусть AD – одна из медиан треугольника (рис. 9). Введем в рассмотрение векторы , 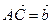и . Тогда . Возведем обе части равенства в квадрат: , то есть . А так как , то . Значит, . В итоге получаем, что и далее .

2.5 Векторное произведение векторов

Три некомпланарных вектора , и , взятые в указанном порядке, образуют правую (левую) тройку, если с конца вектора кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки, (соотв. по часовой стрелке) (см. рис. 11).

Векторным произведением неколлинеарных векторов и называется вектор , определяемый условиями:

1) вектор перпендикулярен векторам и , т.е. , ;

2) длина вектора равна площади параллелограмма, построенного на векторах и как на сторонах, т. е. , ;

3) векторы , и образуют правую тройку.

Векторное произведение обозначается или .

Если векторы и коллинеарны (в частности, один из этих векторов нулевой), то по определению .

Свойства векторного произведения:

1. (антикоммутативность);

2. (ассоциативность по отношению к скалярному множителю);

3. (дистрибутивность);

4. если (или или ).

Для вычисления площади параллелограмма, построенного на векторах и , применяют формулу .

Векторное произведение может быть выражено формулой: , где 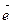– орт направления .

Пример 5:Даны два вектора и , для которых , , . Найти: а) ; б) .

Решение:

а) По формуле находим модуль векторного произведения: . По формуле получаем , где 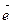– единичный вектор направления .

б) Согласно свойствам векторного произведения получаем:

.

Следовательно, .

2.6 Проекция вектора на ось

Осью называется всякая прямая, на которой выбрано одно из двух направлений (все равно какое). Это направление называется положительным (на рисунке оно обозначается стрелкой); противоположное направление называется отрицательным.

Каждую ось можно задать любым вектором, лежащим на ней и имеющим то же направление. Например, ось на рисунке 133 можно задать вектором или , но не вектором .

Пусть дана ось ОХ (рис. 134) и некоторая точка М (на оси или вне ее). Проведем через М плоскость, перпендикулярную оси. Она пересечет плоскость в некоторой точке М¹. Точка М¹ называется проекцией точки М на ось ОХ. Если точка лежит на оси, то она сама является своей проекцией.

Иными словами, проекция точки М на ось ОХ есть основание перпендикуляра, опущенного из точки М на ось ОХ.

Выражение «проекция вектора на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом).

1. Проекцией геометрической вектора на ось ОХ называется вектор , начало которого есть проекция точки А на ось ОХ, а конец которого, есть проекция точки В на ось ОХ.

Обозначение: или, короче, .

Если ось ОХ задана вектором , то вектор называется также проекцией вектора на направление вектора и обозначается .

Геометрическая проекция вектора на ось ОХ также называется компонентой вектора по оси ОХ.

2. Алгебраической проекцией вектора на ось ОХ (или на направление вектора ) называется длина вектора , взятая со знаком «+» или «–» в зависимости от того, имеет ли вектор то же направление, что и ось ОХ (вектор ) или противоположное.

Обозначение: , .

Замечание. Геометрическая проекция вектора – это вектор, алгебраическая проекция – это число.

Пример 6: Геометрическая проекция вектора (рис. 136) на ось ОХ есть вектор . Его направление противоположно направлению оси, а длина при единице масштаба ОЕ равна 2. Значит, алгебраическая проекция вектора на ось ОХ есть отрицательное число : , .

Если векторы и равны, то их алгебраические проекции по одной и той же оси равны. То же и для геометрических проекций.

Алгебраические проекции одного и того же вектора на две равнонаправленные оси равны. То же и для геометрических проекций. Если оси параллельны, но направлены в противоположные стороны, то алгебраические проекции одного и того же вектора на них не равны. Они отличаются знаком.

Пусть есть вектор, сонаправленный с осью ОХ и имеющий длину 1. Тогда геометрическая проекция (компонента) какого-либо вектора по оси ОХ равна произведению вектора на алгебраическую проекцию вектора по той же оси: .

Пример 7: При обозначениях рисунка 136 вектор . Геометрическая проекция вектора на ось ОХ есть вектор , алгебраическая проекция того же вектора есть число . Таким образом, .

2.7 Основные теоремы о проекциях вектора

Теорема 1. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на эту ось.

Теорема справедлива при обоих смыслах понятия «проекция вектора» и для любого количества слагаемых векторов.

Пример 8: Вектор есть сумма векторов и (рис. 139). Геометрическая проекция вектора на ось ОХ есть вектор . А геометрические проекции векторов и есть соответственно и . При этом . Таким образом, .

Пусть есть единица масштаба. Тогда алгебраическая проекция вектора на ось ОХ равна 4 (длина вектора , взятая со знаком «+»), то есть . Далее (длина вектора , взятая со знаком «–»), а . Имеем: , с другой стороны, . Таким образом, .

Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором: .

Пример 9: Вектор (рис. 140) образует с осью ОХ (на рисунке она задана вектором ) угол 60⁰. Если ОЕ – единица масштаба, то . Тогда .

Действительно, длина вектора (геометрической проекции вектора ) равна 2, а направление совпадает с направлением оси ОХ.

Пример 10: Вектор (рис. 141) образует с осью ОХ угол 120⁰. Длина вектора равна 4. Тогда .

Действительно, длина вектора равна 2, а направление противоположно направлению оси ОХ.

 

 

Вопросы

1. Какая величина называется векторной, а какая скалярной? Приведите примеры.

2. Дайте определение вектора, длины вектора.

3. Какие векторы называются коллинеарными, компланарными? Сонаправленные и противоположно направленнные векторы.

4. Какой вектор называется нулевым, единичным?

5. Дайте определение орта вектора. Какие векторы называют противоположными?

6. Какие векторы называют равными?

7. Что называют углом между векторами?

8. Сумма векторов. Правила треугольника и параллелограмма. Основные неравенства при сложении векторов.

9. Как находится сумма нескольких векторов.

10. Перечислите свойства сложения векторов.

11. Опишите правило параллелепипеда при сложении трех векторов.

12. Что называют разностью двух векторов?

13. Что называют произведением вектора на число?

14. Сформулируйте признаки коллинеарности и компланарности векторов.

15. Перечислите законы умножения вектора на число.

16. Дайте определение скалярного произведения векторов. Перечислите его свойства.

17. Какие векторы называются ортогональными?

18. Что называют правой и левой тройкой векторов?

19. Дайте определение векторного произведения векторов. Перечислите свойства векторного произведения.

20. Как выражается векторное произведение векторов через площадь параллелограмма?

21. Дайте определение оси. Как задать ось вектором? Сформулируйте определение проекции точки на ось.

22. Сформулируйте определение геометрической и алгебраической проекции вектора на ось.

23. Перечислите свойства алгебраической проекции вектора на ось. В чем заключается связь между геометрической и алгебраической проекциями вектора на ось?

24. Сформулируйте основные теоремы о проекциях вектора на ось.