Задачи и упражнения
1.  Покажите, что два графа на рис.2.46 изоморфны.
Покажите, что два графа на рис.2.46 изоморфны.
2. «Три дома и три колодца». Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?
3. Найдите число частичных графов конечного графа с m ребрами.
4. Каково число ребер в полном неориентированном графе с n вершинами?
5. Пусть U – множество положительных целых чисел, на котором задано отношение «a есть делитель b». Постройте граф этого отношения для множества целых чисел от 1 до 20.
6. 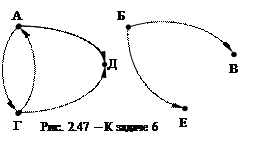 На рис.2.47 задан граф отношения «быть сестрой» на множестве студентов-родственников нашего факультета. Постройте по рис.2.47 граф отношения «быть братом».
На рис.2.47 задан граф отношения «быть сестрой» на множестве студентов-родственников нашего факультета. Постройте по рис.2.47 граф отношения «быть братом».
7. Постройте графы отношений для задач №№ 11 – 17 главы 1.
8. Постройте матрицы смежности и инциденций для правильных многогранников: тетраэдра, куба, октаэдра. Найдите для каждого из них число внутренней устойчивости, число внешней устойчивости, центр, периферийные вершины, радиус, диаметр.
9. Для графа, изображенного на рис.2.48 найдите:
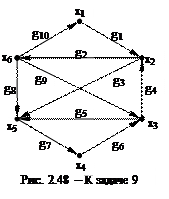 а) матрицу смежности (вершин);
а) матрицу смежности (вершин);
б) матрицу инциденций;
в) наибольшее внутренне устойчивое множество;
г) наименьшее внешне устойчивое множество;
д) матрицу отклонений;
ж) центр и радиус графа.
10. Постройте графы, для которых радиус r равен 2, 3, и такие графы, для которых диаметр d равен 2, 3.
11. Определите, какие из графов трех правильных многогранников имеют эйлеровы циклы. В тех случаях, когда эйлерова цикла нет, определите, сколько требуется цепей, чтобы покрыть все ребра.
12. Какие из графов правильных многогранников имеют гамильтоновы цепи и циклы?