Задачи и упражнения
1. Даны множества X = {1, 2, 3, 4, 5}, Y = {2, 4, 6, 7}, найдите X È Y, X ÇY, X \ Y, Y \ X.
2. Пусть X - множество отличников в группе, Y - множество студентов группы, проживающих в общежитии. Найдите множества: X È Y, X Ç Y, X \ Y, Y \ X.
3. Что представляет собой пересечение множества всех прямоугольников с множеством всех ромбов?
4. Пусть I = {x1, x2, x3} - универсальное множество, а X = {x1, x2}, Y = {x2, x3}, Z = {x3} - его подмножества. Определите перечислением множества: X ´ X, Z ´ Z, X ´ Y, Y ´ X, X ´ Y Ç Y ´ X, X ´ Y È Y ´ X.
5. Проиллюстрируйте графически тождества
X Ç (Y È Z) = (X Ç Y) È (X Ç Z),
X È (Y Ç Z) = (X È Y) Ç (X È Z).
6. Пусть R - множество вещественных чисел, X = {x Î R / 0 £ x £ 1}, Y = {y Î R / 0 £ y £ 2}. Что представляют собой множества X È Y, X Ç Y, X \ Y?
7. Начертите фигуры, изображающие множества A = {(x, y) Î R2 / x2 + y2 £ 1}, B = {(x, y) Î R2 / x2 + (y-1)2 £ 1}, где R2 - вещественная плоскость. Какие фигуры изображают множества A È B, A Ç B, R2 \ A?
8. Пусть X, Y, Z - подмножества множества R2, равные: X = {(x, y) Î R2 / x ³ 0}, Y = {(x, y) Î R2 / y ³ 0}, Z = {(x, y) Î R2 / x + y ³ 1}. Представьте геометрически множества 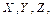




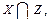
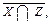


9. Пусть X = {-1, -2, -3, 1, 2, 3, 0} и Y - множество всех натуральных чисел. Каждому числу x Î X ставится в соответствие его квадрат. Выпишите все пары, принадлежащие этому соответствию.
10. Пусть X = {«атом», «стол», «море», «мера»}, Y = {а, м, о, р, е}. Составьте декартово произведение X ´ Y. Отметьте в нем пары, связанные соответствием «в слово x входит буква y».
11. Пусть V - множество положительных целых чисел от 1 до 20, на котором задано отношение R: «число x делится на число y», причем x Î V, y Î V. Выпишите все пары из V, находящиеся в отношении R.
12. Дано множество B = {1, 3, 5, 7, 9}. Элементы этого множества связаны отношением S: «число x на 2 больше числа y». Запишите множество пар, принадлежащих этому отношению.
13. Определите свойства следующих отношений:
а) «прямая x пересекает прямую y» (на множестве прямых);
б) «число x больше числа y на 2» (на множестве натуральных чисел);
в) «число x делится на число y без остатка» (на множестве натуральных чисел);
г) «x - сестра y» (на множестве людей).
14. На множестве X = {x / x Î N, x < 12} задано отношение R: «x и y имеют один и тот же остаток при делении на 5» (x Î X, y Î X). Покажите, что R - отношение эквивалентности. Запишите все классы эквивалентности, на которые разбивается множество данным отношением.
15. Рассмотрите на множестве людей следующие отношения, укажите среди них отношения эквивалентности:
а) «x похож на y»;
б) «x и y живут в одном доме»;
в) «x и y - друзья»;
г) «x живет этажом выше, чем y».
16. Отношение S на множестве X = {1, 2, 3} состоит из пар: (1, 2), (1, 1), (2, 2), (2, 1), (3, 1), (3, 3). Является ли S отношением эквивалентности на множестве X?
17. Какие из нижеперечисленных отношений являются отношениями квазипорядка, порядка, строгого порядка?
а) «отрезок x длиннее отрезка y»;
б) «отрезок x короче отрезка y в 2 раза» - на множестве отрезков;
в) «x старше по возрасту, чем y»;
г) «x является сестрой y»;
д) «x живет в одном доме с y»;
е) «x - друг y» - на множестве людей;
ж) «число x не меньше числа y» - на множестве R;
з) «окружность x лежит внутри окружности y» - на множестве окружностей плоскости.
18. Докажите тождества: A Ç (B \ A) = Æ, A \ (B È C) = (A \ B) \ C.
19. Решите систему уравнений
 A \ X = B,
A \ X = B,
A È X = C,
где A, B, C - заданные множества и B Ì A Ì C.
20. Докажите, что A = B Û (A \ B) È (B \ A) = Æ.
21. Докажите, что если отношения R1 и R2 рефлексивны, то рефлексивны и отношения R1 È R2, R1 Ç R2.
22. Докажите, что если отношения R1 и R2 симметричны, то симметричны и отношения R1 È R2, R1 Ç R2.
23. Докажите, что два множества равны тогда и только тогда, когда результаты их пересечения и объединения совпадают.
24. Известно, что из 100 студентов живописью увлекается 28, спортом - 42, музыкой - 30, живописью и спортом - 10, живописью и музыкой - 8, спортом и музыкой - 5, живописью, спортом и музыкой - 3. Определите количество студентов:
а) увлекающихся только спортом;
б) ничем не увлекающихся.