Выборочных совокупностей (разностный метод).

В группе из 6 больных гипертонией изучалось влияние лекарственного препарата–адельфана, снижающего артериальное давление. В результате опыта получилось 2 вариационных ряда систолического давления: первый – до приема препарата (контроль), второй – после приема (опыт):

контроль 250 240 210 190 185 170

опыт 210 195 165 170 155 175

Необходимо ответить на вопрос: на какую величину снижается верхнее артериальное давление после приема адельфана? Достоверны ли полученные результаты? Проанализируем условия эксперимента. Исследования проводятся на одной группе больных, то есть вариационные ряды значений являются зависимыми (парные наблюдения) и относятся к одной генеральной совокупности. Поэтому статистическую обработку проводим только для контрольной группы ( ). Затем находим разность давлений в контрольном и опытном вариационных рядах (соблюдая знаки) и доказываем, что эта разница статистически достоверна. Для наглядности расчетов данные представляем в таблице 1:

Таблица 1

Контроль АД_к(x_ki)	Опыт АД_о(x_oi)	Разница давлений d_i= АД_о-АД_к
		-40
		-45
		-45
		-20
		-30

Рассчитаем статистические параметры для контрольной группы:

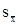=31,9 = =13,02

Аналогично обработаем ряд для разностей давлений:

d_ср = -29,17; D=374,16; s=19,34; s_d=7,90

Определим, достоверно ли определена средняя арифметическая разности давления:

t_эксп= .

Определим по таблице Стьюдента t_табл для Р=0,95 и числа степеней свободы df=n–1=5, t_табл=2,57. t_эксп> t_табл, следовательно, вероятность определения средней арифметической разности d: Р_эксп>0,95. Результаты опыта статистически достоверны.

Сформулируем вывод: верхнее артериальное давление в группе больных гипертонической болезнью составляет 207,5±13,02. Применение лекарственного препарата адельфана привело к снижению артериального давления на =14% с вероятностью P>0,95.