Часть 2

10. Найдите значение выражения .

11. Высота над землёй подброшенного вверх мяча меняется по закону , где h ― высота в метрах, t ― время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трёх метров?

12. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ ребро AA₁ равно 15, а диагональ BD₁ равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A₁ и C.

13. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?

14. Найдите наибольшее значение функции на отрезке .

 

Для записи решений и ответов на задания 15 – 21 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.

15. а) Решите уравнение .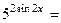

б) Найдите все корни этого уравнения, принадлежащие отрезку .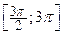

16. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 6, точка K ― середина бокового ребра AP.

а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной плоскости BCP.

б) Найдите угол между плоскостью сечения и плоскостью основания пирамиды.

17. Решите неравенство

18. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что 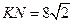и .

19.В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

20. Найдите все такие значения параметра , при каждом из которых уравнение не имеет решений.

21. В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до 20 и два центральных сектора. При попадании в наружный сектор игрок получает количество очков, совпадающее с номером сектора, а за попадание в центральные сектора он получает 25 или 50 очков соответственно. В каждом из наружных секторов есть области удвоения и утроения, которые, соответственно, удваивают или утраивают номинал сектора. Так, например, попадание в сектор 10 (не в зоны удвоения и утроения) дает 10 очков, в зону удвоения сектора ― 20 очков, в зону утроения ― 30 очков.

а) Может ли игрок тремя бросками набрать ровно 161 очко?

б) Может ли игрок четырьмя бросками набрать ровно 235 очков?

в) С помощью какого наименьшего количества бросков, игрок может набрать ровно 947 очков?