Задача 5

В ромбе уравнения двух сторон заданы уравнениями: 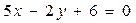и

. Диагонали пересекаются в точке N (5;5). Составить уравнения

двух других сторон ромб . Найти площадь ромба

Дано:

-ромб

,

,

- точка пересечения диагоналей

Составить уравнения сторон, найти площадь.

 

 

Рис.5

 

Решение

1 Найдем координаты точки

 

 

получим ,

 

2 Найдем координаты точки

 

Т.к диагонали ромба в точке пересечения уделяться пополам, то

, откуда ,

, откуда ,

.

3 Составим уравнение стороны АD:

 

Найдем из её общего уравнения : , тогда .

Воспользуемся уравнением «пучка»

 

4 Составим уравнение стороны СD:

Воспользуемся аналогичным алгоритмом, получим:

 

 

5 Найдем площадь ромба

Воспользуемся формулой (*)

5.1 Найдем длину диагонали ВD: ,

 

Воспользуемся формулой вычисления длины отрезка

 

 

5.2 Найдем координаты точек А и С:

получим ,

 

получим ,

5.3 Найдем длину АС

5.4 Найдем площадь ромба

Подставим длины АС и ВД в формулу (*)

(кв. ед)

 

Ответ: , , 24 кв.ед.