Общее уравнение плоскости

Плоскость в пространстве можно задать некоторой точкой и некоторым вектором , перпендикулярным плоскости. Вектор называется нормальным или направляющим вектором плоскости.

 

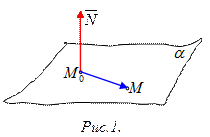
Пусть ‑ произвольная точка плоскости . Вектор целиком лежит в плоскости , поэтому и ‑ перпендикулярные и их скалярное произведение равно нулю:

. (1)

Уравнение (1) называется уравнением плоскости в векторном виде.

В координатной форме уравнение (1) запишется как

или

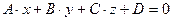, (2)

где .

Уравнение (2) называется общим уравнением плоскости.

Если в уравнении (1) в качестве направляющего вектора плоскости взять единичный вектор , где , то получим нормальное уравнение плоскости:

. (3)

или в координатной форме

. (4)

Задача. Найти расстояние от точки до плоскости , заданной уравнением (3).

Решение.

Если ‑ начало координат и ‑ точка данной плоскости (рис.2), то и . Введем обозначения:

‑ расстояние от начала координат до плоскости, тогда справедливо равенство ;

‑ проекция вектора на вектор , т.е.

;

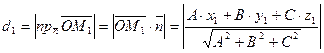‑ расстояние от точки до плоскости .

Так как , то имеем

.