ЦЕНТР ДАВЛЕНИЯ. ФОКУС ПРОФИЛЯ

 

1. Условимся аэродинамические характеристики цилиндрическо­го крыла с заданным профилем в условиях плоскопараллельного обтекания невозмущенным потоком всех его сечений, назы­вать характеристиками профиля крыла.

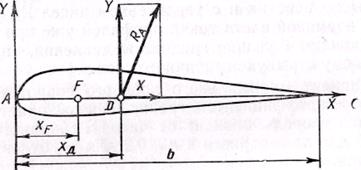
Рис. 13.10, К определению центра давления и фо­куса профиля

 

Точка D, являющаяся точкой пересечения линии действия полной аэродинамической силы с хордой крыла, называется центром давления (рис. 13. 10). Отношение абсциссы центра данления к хорде профиля обозначается через хд=х_Д/b. Для опре­деления абсциссы точки приложения аэродинамической силы нужно знать момент аэродинамической силы относительно какой-либо точки на профиле (например, относительно передней кром­ки профиля).

Момент нормальной силы относительно передней кромки про­филя можно записать в виде

M_z= - Y x_д = -(Y_a cos α + X_a sin α) x_д, (13.18)

откуда находится абсцисса центра давления, отсчитываемая от передней кромки профиля: 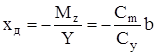(13.19)

Используя же выражения (13.8), (13.9), (13. 17), получим

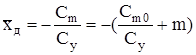(13.20)

Опыты показывают, что в значительной степени для тонких и слабоизогнутых профилей величины С_ya и m почти не зависят от формы профиля, а С_м0 наоборот в значительной степени зависят от формы профиля.

Момент силы Υ относительно произвольной точки F на хорде профиля (см. рис. 13.10) М_F = – Y (х_Д —X_F) = M_z + Yx_F.

 

Переходя от размерных величин к коэффициентам и учиты­вая (13. 7), получим

C_mF = C_m + C_y x_F = c_m0 + m C_y + C_y x_F = C_m0 + ( m + x_F ) C_y. (13.21)

Очевидно, что при х_F = – m коэффициент момента c_mf =c_m0 и не зависит от угла атаки. Характерная для профиля точка F, обладающая тем свойством, что вычисленный относительно нее главный момент сил давления потока не зависит от угла атаки, называется фокусом крыльевого профиля.

Для большинства профилей при малых числах Μ (т.е. без учета сжимаемости) коэффициент m = -0,22...-0,25. Это оз­начает, что х_F = -m = 0,22...0,25 или x_F = (0,22...0,25)b т.е. фокус профиля крыла находится примерно на расстоянии 1/4 хорды от передней кромки. Неизменное положение фокуса на хорде возможно лишь при линейной зависимости c_m = f(c_ya).Для симметричного профиля кривые c_m= f(a) и с_уa = f(а) проходят через начало координат. В таком случае в пределах линейной зависимости из двух треугольников (рис. 13.11) по­лучим: – С_m = a₁ tg j₁ С_ya = a₁ tg j₂ (13.22)

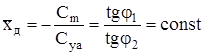(13.23)

Следовательно, для симметричного профиля положение цент­ра давления по углам атаки остается неизменным и совпадает с фокусом профиля

 

 

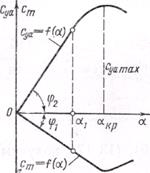
Рис.13.11 Изменение аэродинамических коэф­фициентов cyα и ст в за­висимости от угла атаки α в случае симметрич­ного профиля

 

Рис. 13,12. Изменение коэффициента

центра давления в зависимости от

аэродинамического угла атаки

 

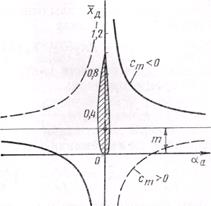
Центр давления несимметричного профиля с изменением уг­ла атаки перемещается вдоль хорды или ее продолжения от минус бесконечности до плюс бесконечности (рис. 13, 12), Гра­фически зависимость х_Дот аэродинамического угла атаки а_а изображается равнобочной гиперболой. В случае с_m<0 {сплошная линия) центр дав­ления с возрастанием угла атаки 'перемещается к носику профиля, а в случае с_m>0

(пунктирная линия) — к хвостику.

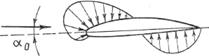
Рис. 13.13. Распределение аэродина­мической нагрузки по профилю при угле нулевой подъемной силы a0

При α = α₀ (что соответствует с_уа=0) центр давления нахо­дится на бесконечности, так как при отсутствии подъемной силы аэродинамическое воздействие на такой профиль приводится к паре сил (рис. 13. 13).

13.7. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ ПО ПРОФИЛЮ

 

Для расчета крыла на прочность, кроме величии коэффици­ентов c_xa, Суa, с_т необходимо знать распределение давления по профилю. Распределение давления по профилю изображается графически в виде координатной или векторной диаграмм. Коор- динатная диаграмма строится в системе координат, где по оси абсцисс откладывают относительные расстояния x=x/b (b — хорда профиля), а по оси ординат — коэффициент давления р = =Ap/q_oo, где Ар=р — рoo и qoo =ro *V2/2.

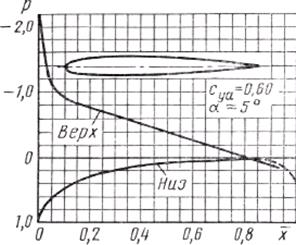
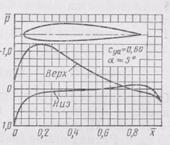
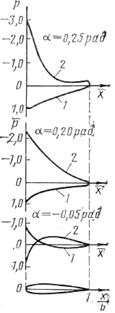Эпюры распределения давления (координатные диаграммы) для несимметричного профиля при различных углах атаки α (α= —0,05; 0,20; 0,25 рад) изображены на рис. 13, 14. Эти эпю­ры получены при малых числах М, т. е. без учета сжимаемости потока жидкости.

Рис. 13.14. Эпюры распределения давления по несимметричному профилю на раз­личных углах атаки: 1 -верхняя поверх­ность профиля; 2 - нижняя поверхность профиля

В критической точке р=1 (для сжимаемой жидкости p>l). При отрицательных углах атаки эта точка лежит на верхней поверхности профиля, а при а>0 переходит на нижнюю сторону. На верxней и нижней поверхностях вблизи носика профиля происходит интенсив­ное ускорение потока с соответствующим сни­жением давления, при этом снижение давле­ния на верхней стороне профиля происходит более интенсивно, чем на нижней. Эти участки профиля являются конфузорными. За точками минимума давления поток замедляется, а дав­ление повышается. Эти участки у профиля яв­ляются диффузорными. На задней кромке про­филя, где происходит слияние струй, сбегаю­щих с верхней и нижней поверхностей про­филя, полное давление не восстанавливается, так как в пограничном слое имеют место необ­ратимые потери давления.

Если местные скорости больше Voo, то рмeст<Рoo и Др<0. В этом случае понижение давления называется подсосом. Если Vмеcт < <Voo, то р_мест >Рoo и Др>0. Это повышение давления называется подпором. В точках, где местная скорость достигает скорости невозму­щенного потока, коэффициент давления равен нулю.

На углах атаки, больших 0,05 рад, подсос обычно распространяется почти на всю верх­нюю поверхность, а подпор—на всю нижнюю.

Из приведенных эпюр распределения давления (см. рис. 13. 14) можно заключить, что при малых положительных углах атаки понижение давления на верхней поверхности значительно больше по абсолютной величине по сравнению с повышением давления на нижней поверхности, следовательно, в этом случае аэродинамическая подъемная сила профиля создается главным образом за счет подсоса на верхней поверхности и в меньшей мере – за счет подпора на нижней.

Следует отметить, что для сжимаемой среды это положение справедливо при малых скоростях движения, при сверхзвуковых скоростях вклады верхней и нижней поверхностей в создание подъемной силы могут быть одинаковыми. При увеличении уг­лов атаки до критических картина распределения давлений по верхней поверхности существенно изменяется: подсос на верхней стороне достигает очень больших значений (p = – 2 ... – 3 ), в то время как подпор на нижней стороне по-прежнему харак­теризуется величиной р <1. В этом случае на верхней по­верхности профиля появляются значительные диффузорные участки, где возникают большие положительные градиенты давления, которые, как известно, вызывают отрыв пограничного слоя.

 

 

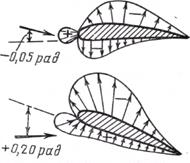
Рис. 13.16, Векторные диаграммы

Рис. 13.15 Схема обтекания профиля на критическом угле атаки: 1 – безотрывное обтекание; 2 – обтекание при наличии отрыва (т – точка отрыва пограничного слон)

распределения давлений

 

Схема обтекания профиля на критическом угле атаки, а так­же эпюры распределения давлений с отрывом пограничного слоя для потока несжимаемой жидкости показаны на рис. 13. 15.

Точка минимума давления у дозвуковых профилей с относи­тельной толщиной с=10... 14%, располагается на верхней по­верхности вблизи передней кромки профиля. Это способствует раннему переходу ламинарного пограничного слоя в турбулент­ный, а при больших предкритических углах атаки у профилей с тонким «носиком» приводит к срыву потока.

На векторной диаграмме распределения давления безразмер­ный коэффициент давлений ρ изображается в виде стрелок-век­торов, направленных по нормали к поверхности профиля (рис. 13. 16). Область подсоса разрежения обозначается зна­ком «минус», а область подпора — знаком «плюс», при этом под­сос указывается стрелками, направленными в сторону внешней нормали, а подпор — в сторону внутренней. Из рисунка видно, что при малом угле атаки а= а₀ на верхней стороне профиля у передней кромки имеется подпор, который переходит в подсос. На нижней стороне наблюдается обратное явление.

 

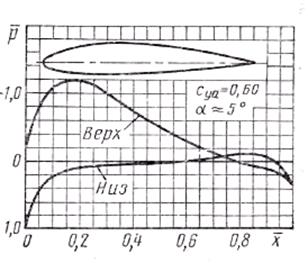
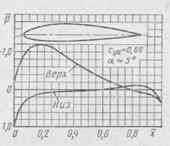
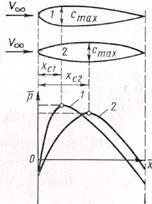Рис. 13.17, Эпюры распределения давлений

по двум профилям различной толщины

 

Эпюры давлений позволяют построить график распределения нагрузки от сил давления по хорде профиля.

Рис. 13.18. Влияние поло­жения максимальной тол­щины профиля на картину распределения давления

Если вектор ρ проектируется на хорду и проекции откладываются вдоль ординаты, соответствующей точке максимальной толщины про­филя, то полученные таким образом эпюры нагрузок позволяют опреде­лить коэффициент с_x без учета сил трения.

На картину распределения дав­ления по профилю значительное влияние оказывает форма профиля; относительная толщина (рис. 13.17), положение точек максимальной тол­щины и кривизны. При малых углах атаки со смещением абсциссы х_с сдвигается и точка минимального давления на профиле (рис. 13.18).