АЭРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТ

Взаимодействие между газом (воздухом) и движущимся в нем крылом приводит к возникновению непрерывно распреде­ленных по всей поверхности крыла так называемых аэродинами­ческих сил, которые могут быть охарактеризованы величинами нормального ρ и касательного t напряжений в каждой точке поверхности крыла.

Результирующая сил давления и трения, возникающих при движении летательного аппарата относительно воздушной среды, сила , называется полной аэродинамической силой. Часто под полной аэродинамической силой понимают только ре­зультирующую нормальных сил, пренебрегая при этом силами трения.

Момент полной аэродинамической силы относительно перед­ней кромки крыла M_z называется продольным моментом или аэродинамическим моментом тангажа. Момент М_г считается по­ложительным, если он стремится повернуть крыло в сторону уве­личения угла атаки а, и отрицательным – в обратную сторону. Положительный момент называется кабрирующим, а отрица­тельный – пикирующим.

При теоретическом и экспериментальном исследованиях си­лового взаимодействия движущегося тела с окружающей его средой обычно рассматривается не результирующая сила R_A, а проекции этой силы на оси той или иной системы координат, которая выбирается в зависимости от условий задачи. В аэроди­намике чаще используются две системы координат: скоростная и связанная.

В скоростной системе координат ось ОХ_а совпадает с направ­лением скорости полета, ось OY_a перпендикулярна к оси ОХ_а и лежит в плоскости симметрии летательного аппарата. Ось ОZ_a составляет с осями Ох_а и ОУ_a правую систему координат (на­правлена вдоль правого крыла). При аэродинамических расчетах начало координат обычно совмещают с передней кромкой крыла.

В связанной системе координат ось ОХ направлена вдоль хорды крыла или продольной оси самолета, ось ΟΥ перпендику­лярна оси ОХ и лежит в плоскости симметрии летательного ап­парата, ось ΟΖ составляет с осями ОХ и ΟΥ правую систему. В скоростной системе координат проекции силы R_А обозна­чаются Х_а, Υ _а, Z_a, а в связанной Χ, Υ, Ζ (рис. 13.2). При рассмотрении плоских течений аэродинамическая сила раскладывается на две составляющие Х_а, Υ_α (Χ, Υ).

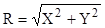или 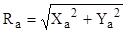(13.1)

В скоростной системе координат проекция силы R_A на на­правление, перпендикулярное к скорости невозмущенного пото­ка, называется аэродинамической подъемной силой Y_a , а проек­ция силы ra на направление, противоположное движению кры­ла (самолета), называется лобовым сопротивлением Х_а.

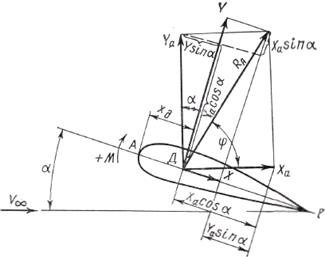
Рис. 13.2. Составляющие полной аэродинами­ческой силы

в скоростной и связанной систе­мах координат

В связанной системе координат силы У и X называются аэродинамической нормальной и продольной силами соответст­венно.

Составляющие силы в этих двух системах координат связа­ны между собой следующими зависимостями (см. рис, 13.2):

Y = Y_асоs a + X_a sin a; Х = Х_а cos a — Y_а sin a (13.2)

или Y_a = Ycos a— X sin a; X_a = X cos a + Y sin a (13.3)

Рассмотримсилы, действующие на цилиндрическое крыло бесконечного размаха, обтекаемое потоком жидкости, в связан­ной системе координат, начало которой находится на расстоянии х_с от передней кромки крыла (рис. 13.3). Выделим в качестве характерной длины отрезок крыла длиной l и характерной пло­щади – площадь S=lb(b – длина хорды).

Сила давления, действующая на элемент поверхности крыла l×dS равна p×l×dS, а проекции этой силы на оси ОХ и OY: dY = p×cosb×l×dS = ± l×p×dx; dX = p×l×sinb×dS = l×p×dy.

Для определения сил X и Υ необходимо просуммировать эле­ментарные составляющие по всему контуру профиля. Вдоль оси ОХ суммирование производим отдельно для верх­ней и нижней частей профиля, вдоль оси О У — для передней и задней. Тогда для нормальной и продольной сил получим: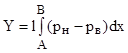

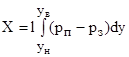
где р_п, р_э, р_н, р_в – соответственно давление на передней, задней, нижней и верхней частях профиля.

 

Рис. 13.3. К расчету подъемной силы и лобового сопротивления

 

Действительная аэродинамическая продольная сила будет больше расчетной на величину равнодействующей сил трения на поверхности крыла. По величинам Y и X для каждого угла атаки с помощью фор­мул связи (13.3) можно определить подъемную силу Y_а и силу лобового сопротивления Х_а.

По опытным данным продольная сила X и толщина профиля малы по сравнению с нормальной силой Y и хордой профиля, поэтому моментом от продольной силы ввиду его малости обыч­но пренебрегают. Зная элементарный момент от нормальной силы

dM_z = – dY×x = – ( р_н – р_в)×l×xdx,

можно определить и полный момент крыла относительно пе­редней кромки профиля

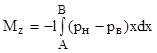(13.6)

 

3.3. АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ

И КАЧЕСТВО ПРОФИЛЯ

Общие формулы для определения подъемной силы и силы лобового сопротивления крыла Y_a = с_ya×q×S X_a = cxa×q×S (13.7)

где – скоростной напор или динамическое давление невозмущенного потока; с_уa – коэффициент подъемной силы; С_ха – коэффициент лобового сопротивления; S – несущая пло­щадь крыла; V_¥ – скорость потока на бесконечности.

Соответственно формулы для нормальной и продольной сил имеют вид

Y = Cy×q×S·, X = Cx×q×S, (13.8)

где С_у, C_х — коэффициенты нормальной и продольной сил.

Если обозначить коэффициент полной аэродинамической си­лы через C_rа, а коэффициент полного момента относительной передней кромки профиля через C_m, то

Ra = C_RА×q×S; M_z = Cm×q×S×b, (13.9)

где b — условное плечо момента (обычно хорда профиля). С уче­том формул (13.1) и (13,8) получим

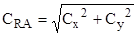(13.10)

В формулах (13.2) и (13.3) от сил можно перейти к их ко­эффициентам

C_y = C_ya cos a +C_xa sin a; C_х = C_ха cos a – C_ya sin a. (13. 13)
и C_ya = C_y cosa – C_x sin a; C_xa = C_x cos a + C_y sin a. (13.12)

 

Углы атаки, реализуемые в полете, обычно невелики, поэто­му можно положить cosa = l, sin a = a. Учитывая, что на прак­тике коэффициент сопротивления с_ха обычно на порядок меньше коэффициента подъемной силы C_уа, формулы (13. 11) и (13. 12) можно привести к более простой и чаще употребляемой форме:

C_ya = C_y C_xa= C_х+ C_у×a, (13. 13)

C_y = C_ya C_х = C_xa – C_yа×a. (13.14)

Используя выражение (13.4), формулу для определения ко­ ко­эффициента нормальной силы профиля представим в виде

 

Аналогично для коэффициента C_m можно записать

При малых углах атаки коэффициент подъемной силы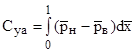

Таким образом, по распределению давления на нижней и верхней сторонах профиля, можно определить его коэффициент подъемной силы. Для практической реализации этого метода расчета необходимы экспериментальные исследования с дрени­рованной моделью профиля при условии обтекания, соответст­вующем бесконечному размаху крыла (плоское обтекание).

Чаще аэродинамические коэффициенты определяются весо­вым методом, для чего на специальных весах измеряются непо­средственно в потоке аэродинамической трубы силы и моменты, действующие на модель крыла, а затем расчетным путем опреде­ляются коэффициенты.

Для оценки аэродинамических свойств профиля вводится по­нятие о качестве профиля К. Аэродинамическим качеством про­филя называется отношение подъемной силы к силе лобового сопротивления: K=Y_a/X_a или через аэродинамические коэффи­циенты К=C_уa/C_xa. Эта величина представляет собой тангенс угла наклона полной аэродинамической силы R_A к направлению невозмущенного потока, т.е. K = tg j . Чем меньше лобовое сопротивление при той же подъемной си­ле, тем больше качество.

Безразмерные величины C_хa, C_уа, C_m, с_ra и К. являются основ­ными аэродинамическими коэффициентами профиля крыла.

 

13.4. ЗАВИСИМОСТЬ АЭРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ ОТ УГЛА АТАКИ ПРОФИЛЯ. ПОЛЯРЫ ПРОФИЛЯ

Аэродинамические коэффициенты с_ха, с_уа и с_т являются неза­висимыми друг от друга величинами, а C_RA и К определяются через коэффициенты с_уа и с_уа по соответствующим формулам. Коэффициент полной аэродинамической силы с_ла, а также· его компоненты с_ха и с_уа, коэффициент момента с_т и аэродина­мическое качество К зависят от формы профиля, угла атаки, критериев подобия Re, M, степени турбулентности потока и др. Этими коэффициентами удобно пользоваться поскольку для ди­намически подобных течений они одинаковы, поэтому же резуль­таты экспериментальных исследований приводятся в виде зави­симостей для аэродинамических коэффициентов. Для данного профиля при фиксированных значениях чисел Re и Μ изменение угла атаки a влечет за собой интенсивное изменение аэродина­мических коэффициентов профиля.

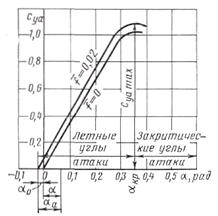
Типичные кривые зависимости аэродинамических коэффици­ентов подъемной силы с_уа. от угла атаки α при малых скоростях обтекания, когда влиянием сжимаемости газа можно пренебречь, приведены на рис. 13. 4.

Опыт и теория показывают, что на углах атаки, при которых сохраняется безотрывное обтекание (a£0,17... 0,25 рад), эти зависимости прямолинейны. На больших углах атаки, когда при увеличении градиен­та давления вдоль профиля крыла начинается отрыв пото­ка, линейная зависимость C_ya=f(a) нарушается, коэффициент Суа увеличивается медленнее и после достиже­ния максимального значения (С _{уа mах} ) уменьшается. Для обычных профилей величина сya mах колеблется в пределах 0,9—1,4.

Угол атаки, при котором величина коэффициента подъемной силы достигает макси­мального значения, называется критическим углом атаки а_kр. Критический угол атаки совре­менных самолетов составляет примерно 0,25 – 0,35 рад. У крыльев малых удлинений а_кp зна­чительно больше.

Величина а_кр в значительной мере зависит от числа Re: с уве­личением числа Re величина а_кр и c_{ya max} возрастают. Углы ата­ки, большие критического, называются закритическими углами атаки. Угол атаки, при котором c_ya = 0, называется углом нулевой подъемной силы и обозначается a0. Он обычно отрицателен и не­велик (a₀ = -0,02 ... -0,05рад). У симметричных профилей α0 = 0. Величина а_кр зависит от относительной кривизны профиля. Чем больше кривизна профиля 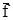, тем левее проходит график С_ya= f(a) (см. рис. 13.4).

Разность между критическим углом атаки и углом нулевой подъемной силы называется диапазоном летных углов атаки. Линия, проведенная из задней кромки профиля в направле­нии, при движении вдоль которого с_уа=0, называется аэродина­мической хордой профиля, а углы атаки, отсчитываемые от этого направления, называются аэродинамическими углами атаки и обозначаются а_а (см. рис. 13. 1)

На прямолинейном участке кривой c_ya = f(a) величина коэф­фициента подъемной силы определяется уравнением С_уа = С^а_уа(а-а₀), где C ^a_ya — угловой коэффициент прямолинейного участка графи­ка c_ya=f(a). Изменение коэффициента нормальной силы c_v в зависимости от угла атаки подобно изменению коэффициента с_уа.

 

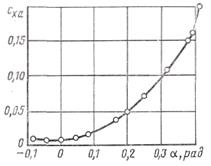
Рис. 13.5. Изменение Рис. 13.6.Изменение

аэродинамичес­кого коэффициента аэродина­мического качества

сопротивления профиля крыла cxa профиля крыла в зависимости

в зависимости от угла атаки α от угла атаки

 

Коэффициент момента с_т является функцией коэффициента подъемной силы с_уа, и на углах атаки, соответствующих безот­рывному обтеканию профиля, определяется уравнением прямой

C_m = C_m0 + mC_уa (13.17)

где C_m0 — коэффициент момента при C_ya = 0, зависящий от кри­визны профиля f;

m = dc_m/dc_ya — угловой коэффициент линей­ного участка графика с_т=f(^суа)·

Зависимость коэффициента лобового сопротивления C_xa от уг­ла атаки α имеет обычно вид параболы (рис. 13.5): сначала C_xa изменяется незначительно (в области летных углов), а затем на­чиная с углов атаки, несколько меньших а_кр, быстро возрастает, что обусловлено усилением отрыва пограничного слоя.

При некотором значении α коэффициент C_xa достигает мини­мального значения C_{xa min}. У симметричного профиля C_{xa min} дос­тигается при а=0 , а у несимметричного с f<0 – при отрица­тельном значении угла атаки, близком к углу нулевой подъем­ной силы.

Характер изменения коэффициента с_х в зависимости от угла атаки в значительной мере отличается от характера изменения C_xa =f(α). Аэродинамический коэффициент C_х на больших поло­жительных углах атаки в отличие от коэффициента C_xa может стать отрицательным (см. формулу 13. 11).

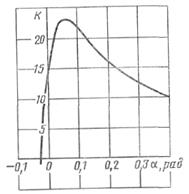
Аэродинамическое качество профиля крыла также зависит от угла атаки (рис. 13.6). Для профилей крыльев максимальное значение качества K_mах достигает порядка 25. Угол атаки α = α_HΒ, при котором качество имеет максимальное значение, называется наивыгоднейшим углом атаки. При угле атаки, равном a₀ , каче­ство равно нулю.

 

Pис. 13.7. Поляра I рода Рис. 13.8, Поляра II рода

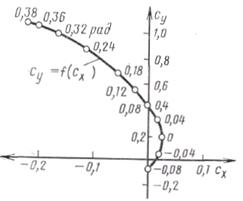
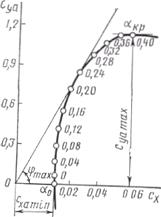
Большое практическое значение имеют зависимости с_yа= f(с_xа), c_y=f(c_x), называемые соответственно полярами I (рис. 13.7) и II (рис. 13.8) рода, поскольку позволяют опреде­лить величину и направление аэродинамической силы. Каждая точка поляры соответствует определенному углу атаки a.

При одинаковых масштабах вдоль осей с_ха и с_уа вектор, сое­диняющий начало координат с той или иной точкой поляры I ро­да, представляет собой по величине и направлению коэффициент результирующей аэродинамической силы, соответствующей дан­ному углу атаки а. Поэтому поляру можно рассматривать как полярную диаграмму в координатах с_rа и а. Так как в диапазоне летных углов атаки коэффициент с_уа в несколько раз боль­ше коэффициента с_xa, то обычно масштаб вдоль оси с_ха выби­рается в 5—10 раз крупнее, чем вдоль оси c_ya.

Отметим характерные точки поляры (см. рис. 13. 7):

- точка максимального аэродинамического качества К_mаx = (С_уа/С_ха)_maхи, следовательно, а_нв. Графически эта точка опре­деляется касательной, проведенной к поляре из начала коорди­нат. Действительно K = tg j, и K_max = tg j _max, т. е. K_max соответ­ствует случаю, когда вектор с_ra совпадает с касательной;

- точка минимального коэффициента сопротивления, обычно соответствующая режиму максимальной скорости в горизонталь­ном установившемся прямолинейном полете;

- точка максимального коэффициента подъемной силы при α=α_κρ.

Полярой второго рода удобно пользоваться при расчетах устойчивости и прочности.

13.5 ЗАВИСИМОСТЬ АЭРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ

ОТ ЧИСЛА Re, СТЕПЕНИ ТУРБУЛЕНТНОСТИ ПОТОКА

И ФОРМЫ ПРОФИЛЯ

Для данного профиля при неизменных числах Μ степени тур­булентности потока ε, угле атаки а коэффициент минимального лобового сопротивления в значительной степени зависит от чи­сел Рейнольдса. У профилей средних относительных толщин (с=10... 15%) с увеличением числа Рейнольдса с_{ya mаx} увели­чивается. При небольших значениях чисел Re величина коэффи­циента Суa max обусловлена отрывом ламинарного пограничного слоя. С увеличением числа Re точка перехода ламинарного по­граничного слоя в турбулентный обычно смещается вверх по течению и, следовательно, происходит отрыв уже турбулентного пограничного слоя. Зона срыва при этом уменьшается и коэф­фициент c_{ya max} увеличивается.

У тонких профилей (с = 5... 6%) и профилей с заостренным носиком коэффициент С_{ya max}с изменением числа Re остается почти постоянным, так как отрыв потока у тонких профилей про­исходит вблизи передней кромки профиля и при малых углах атаки.

У очень толстых профилей (с=15... 20%) коэффициент cya max обычно невелик и с увеличением чисел Re уменьшается, так как в кормовой части таких профилей уже при малых углах атаки возникают большие градиенты давления, приводящие к более раннему отрыву пограничного слоя.

Коэффициент минимального лобового сопротивления c_{xa min} определяется коэффициентом трения плоской пластины С_f, кото­рый, в свою очередь, зависит от числа Рейнольдса: Cf~l/Reⁿ, где n=0,5 для ламинарного и n = 0,2 для турбулентного погра­ничного слоя.

Очевидно, что с увеличением числа Re уменьшается коэффи­циент минимального лобового сопротивления.

С возрастанием начальной степени турбулентности потока коэффициент С_{xa min} увеличивается, коэффициент С_{ya max}тонких и толстых профилей изменяется незначительно; коэффициент C_{ya mах} у профилей средних толщин увеличивается. Такое влия­ние начальной турбулентности потока на аэродинамические ха­рактеристики профиля объясняется изменением положения точки перехода ламинарного пограничного слоя в турбулентный с увеличением начальной степени турбулентности.

Рис, 13.9, Изменение коэффициента Cya max в зависимости от кривиз­ны f и абсциссы xf

Существенное влияние на аэродинамические коэффициенты профиля оказывают геометрические параметры профиля. С уве­личением относительной тол­щины профиля происходит увеличение коэффициента ми­нимального лобового сопротив­ления Сxа min. Коэффициент максимальной подъемной силы с_уa max с возрастанием увеличивается, а в диапазоне 12—20% -уменьшается. Влияние на коэффи­циент максимальной подъемной силы Cya max дозвукового профиля большой относитель­ной толщины показано на рис, 13-9.

 

С увеличением относительной кривизны профиля f коэффици­ент c_{xa min} (у профилей средних толщин), коэффициент с_т и угол нулевой подъемной силы (по абсолютной величине) возрастают.