Простые машины.

Рычаг. Рычаг находится в равновесии, когда действующие вращательные моменты равны и противоположны.

Рычаг первого рода (рис.21): Рр = Qq.

Рычаг второго рода (рис.22): Рр – Qq = 0.

Изогнутый рычаг объединяет изменение направления силы с изменением ее

величины (рис.23)

Применения. Рычаг второго рода: предплечье, тачка, щипцы для орехов, предохранительный клапан паровой машины. Рычаг первого рода: клещи, ножницы, рычажные весы.

Ворот и лебедка. Ворот (рис.24) состоит из двух соединенных наглухо блоков, сидящих на общей оси. Закон рычага выражает условие равновесия:

P · R = Q · r или P = Q · r ׃ R

У лебедки большой блок ворота заменен рукояткой (R). С канатным барабаном (r) связано

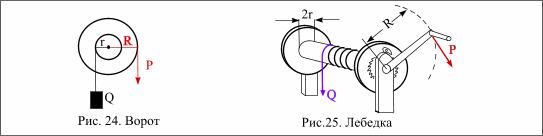
зубчатое колесо, которое сцепляется с запорной щеколдой, чтобы рукоятка не могла развернуться в обратную сторону (рис.25)

Блок. (рис.26). Неподвижный блок служит только для изменения направления силы, он не дает выигрыша в силе. Подвижный блок уменьшает силу в два раза, половину веса груза принимает на себя точка подвеса. При наклонно прикрепленном канате выполняется правило параллелограмма :

Полиспасты. Полиспасты представляют систему блоков, соединенных в общем держателе.

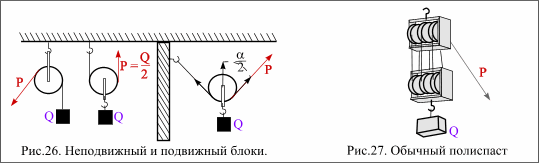
Обычный полиспаст c n – неподвижными и n – подвижными блоками (рис.27) :

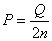
Пояснение. Представим себе, что трос между блоками разрезан; каждый его конец испытывает нагрузку Q/2n; следовательно, также и тот конец, к которому приложена сила Р.

 

Степенной полиспаст (рис.28): Р = Q/2n

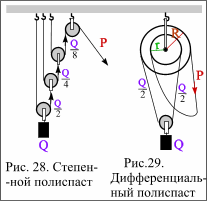Пояснение. Каждый подвижный блок делит нагрузку пополам. Степенной полиспаст малоупотребителен из-за своей громоздкости.

Дифференциальный полиспаст (рис.29).

Р = (R - r)•Q/2R.

Пояснение. Вращающие моменты:

(Q • r)/2 + PR = (Q • R)/2

Для всех простых машин пригодно золотое правило механики:

Что выиграно в силе, то проиграно в пути; ни выигрыша, ни проигрыша в работе не происходит. Машины служат для изменения условий работы, но не дают выигрыша в работе.

Весы. Рычажные весы подчиняются законам рычага.

Равноплечие весы. Устойчивое равновесие, центр тяжести под центром вращения. Чувствительность весов растет вместе с длиной коромысла и убывает с возрастанием веса коромысла (коромысло делают решетчатым).

Чувствительность измеряется при помощи перегрузка Х, дающего некоторое отклонение α (рис.30). d = s sin α, p = l sin α, (P + X)p = Pp + Gd;

G – вес коромысла, l – длина плеча коромысла, s – расстояние центра тяжести от оси вращения. Взвешиваемый груз Q кладется один раз на левую чашку весов и один раз на правую; находятся значения Р1 и Р2, пусть длины плеч равны x и y (рис.31):

Q·x = P1·y, P2·x = Q·y, Q׃P2 = P1׃Q, Q² = P1· P2, Q = √(P1· P2)

Истинным значением веса является среднее геометрическое их обоих взвешиваний. Для практических целей применяется в большинстве случаев среднее арифметическое, которое несколько больше, чем среднее геометрическое.

Неравноплечие весы (безмен) (рис. 32) Взвешиваемый груз подвешивается на короткий конец рычага; подвижный грузик находится на длинном плече.

Почтовые весы (рис. 33) При нагрузке весов чашка их может перемещаться только в вертикальном направлении, так как ее ось составляет часть шарнирного параллелограмма. Верхняя сторона параллелограмма является одновременно коротким плечом изогнутого рычага, длинное плечо которого утяжелено на конце. Длинное плечо скользит по шкале. В случае равновесия оба вращающих момента равны и противоположны.

Десятичные весы (рис. 34). На десятичных весах гири уравновешивают десятикратный груз. Правое плечо рычага первого рода АВ разделено в таком же отношении, как рычаг второго рода О1D; левое плечо рычага АВ в десять раз превышает длину одного деления шкалы, нанесенной на правом плече. Для рычага первого рода получается следующее уравнение моментов: Х ·10 = Q ·1 + Rn.

Для рычага второго рода: 0 = Rn - Р·1, Х ·10 = Q + Р = L.

Наклонная плоскость. (рис. 35)

Крутизна: tg α = h / b; сила (скатывающая), действующая вдоль наклонной плоскости

Н = G sin α = G·h / l. Сила давления на плоскость N = G·cos α = G·b/ l.

Нагрузка : силе давления : силе скатывания = длина : основанию : высоте.

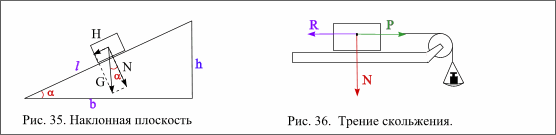
Трение. Силы трения представляют силы сопротивления, которые проявляются, когда начинает действовать какая- либо другая сила. Сила трения противодействует силе скатывания. различают два вида трения: трение скольжения (рис.36) и трение качения.

Коэффициент трения μ есть отношение силы трения к силе давления на поверхность:

μ = R : N.

μ может быть определено при помощи наклонной плоскости с переменным углом. Брусок начинает скользить, если Н равно R; μ = (G sin α) :(G·cos α) = tg α ;

R = μ N

Сила трения не зависит от величины соприкасающихся поверхностей.

Коэффициенты трения.

Дерево по металлу 20 ± 48%, при смазке 6 ± 18%.

Металл по металлу, сухой 15 ± 24% , при смазке 6 ± 11%.

Металл по льду 2 ± 3%.

Трение качения: металл по металлу 1%.

Винт и клин. При одном обороте винт смещается на свой шаг h. Шаг винта может быть вычислен по свойствам наклонной плоскости (рис.37). Из золотого правила механики следует P· 2 πR = Q· h

P = (Q· h) : (2 πR.)

Винты находят применение в давящих и подъемных приспособлениях (прессы, шлюзовые затворы) и прежде всего как скрепляющие винты, вследствие большого трения, возникающего при вращении винта.

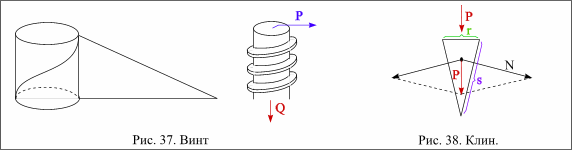
Клин (рис.38) состоит из двух наклонных плоскостей, сложенных основаниями. Сила Р, действующая на основание клина, может быть разложена на две равные нормальные компоненты N. Из подобия треугольников следует Р : N = r : s.

Р = N (r : s)

Чем острее угол клина, тем бо́льшую разрушающую силу можно получить.