Сложные проценты

В долгосрочных финансово-кредитных операциях (п >> 1), если проценты не выплачиваются сразу же после их начисления, а присоединяются к сумме долга (капитализируются), как правило, применяют сложные проценты (compound interest). База для начисления сложных годовых процентов увеличивается в конце каждого года, и процесс увеличения суммы долга обычно происходит быстрее, чем в схеме простых процентов.

Рис. 3. Наращение по схеме сложных процентов.

Наращенная сумма долга по годовой ставке сложных процентов за п лет определяется формулой

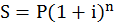, (1.10)

где (1 + i)ⁿ - множитель наращения по годовой ставке сложных процентов.

Из (1.10) вытекает, что современная величина

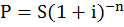, (1.11)

где (1 + i)^-ⁿ — дисконтный множитель по годовой ставке сложных процентов.

Если ставка сложных процентов меняется от периода к периоду (на периоде длительностью п_k действует ставка сложных процентов i_k), наращенная сумма

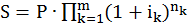. (1.12)

Разрешая формулу (1.12) относительно Р, можно найти современную величину S по плавающей ставке сложных процентов.

Если срок п для начисления сложных процентов не является целым числом, т.е. п = а + b, где а - целое число лет, а b — дробная часть года, 0<b<1, то для вычисления наращенной суммы можно использовать два метода. Согласно общему методу (его также называют приближённым), расчет ведется непосредственно по формуле (1.10). По смешанному методу (называемому точным), за целое число лет начисляют сложные проценты, а за дробную часть года - простые, т. е.

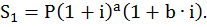(1.13)

Смешанный метод дает большее значение наращенной суммы, чем общий метод, т. е S₁>S.

Проценты могут капитализироваться по сложной годовой ставке i не один, а m раз в году, через равные промежутки времени 1/т. В таком случае для вычисления наращенной суммы можно использовать формулу (1.10), в которой под ставкой i следует понимать ставку процентов за период j/т, а n будет обозначать число n∙m от таких периодов, т.е.

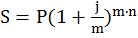, (1.14)

где 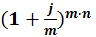- множитель наращения по номинальной ставке j с m-разовым начислением процентов в год.

Из (1.14) получаем, что современная величина S равна

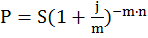, (1.15)

где 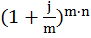- дисконтный множитель по номинальной ставке j.

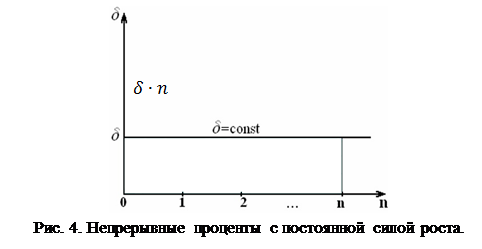
Непрерывные проценты

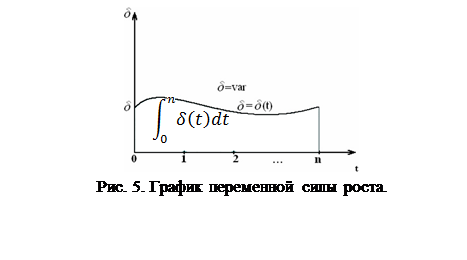
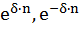Если устремить m к бесконечности, то промежуток 1/m между начислениями процентов будет стягиваться к нулю, и проценты будут начисляться непрерывно. Для того чтобы отличить непрерывную ставку от дискретной, номинальную ставку j обозначим через S. Ставку S называют непрерывной ставкой процентов или силой роста. В результате предельного перехода в (1.14), (1.15) получаем где - соответственно множители наращения и дисконтирования по годовой постоянной ставке непрерывных процентов .

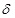Если сила роста изменяется во времени, т.е. 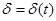, то наращенная сумма и современная стоимость определяются как

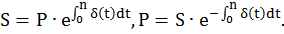(1.16)

По аналогии с номинальной ставкой сложных процентов вводится номинальная учетная ставка f с m-разовым дисконтированием в году, т.е. каждый раз по ставке f/m. В таком случае

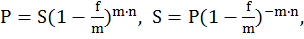(1.17)

где 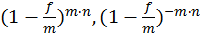- соответственно, дисконтный множитель и множитель наращения.

Пример 1.1.1. На годовой депозит можно положить денежные средства под 10% годовых, а на полугодовой - под 9,75% годовых. Что выгоднее, положить свободные денежные средства на годовой депозит, или два раза воспользоваться полугодовым депозитом, не снимая проценты? Чему будет равна выгода, если имеется 100 тыс. $ и одним потерянным днём при переоформлении депозита можно пренебречь?

Если денежные средства положить на годовой депозит, то наращенная сумма S = 100 • 1,1 = 110 тыс. $. Если два раза воспользоваться полугодовым депозитом, то наращенная сумма Выгоднее воспользоваться годовым депозитом и выигрыш S – S₁= =12,34$.

Пример 1.1.2. На сумму долга в течение 4 лет начисляются проценты по ставке 9% годовых. Насколько возрастёт наращенная сумма, если проценты будут капитализироваться поквартально?

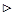При ежегодной капитализации процентов множитель наращения равен 1,09⁴, а при ежеквартальной капитализации - 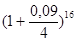т.е. он будет больше в 1,011363032 раза.

Наращенная сумма увеличиться на 1,136%.

1.2. Определение срока платежа и уровня процентных ставок

При разработке условий финансовых операций часто сталкиваются с необходимостью определения одного из параметров сделки: продолжительности ссуды, или уровня процентной ставки при условии, что остальные параметры фиксированы. Подобные задачи легко решаются, если формулы наращения разрешить относительно интересующего нас параметра. Так, исходя из формулы (1.10), годовая ставка сложных процентов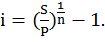

Пример 1.2.1. Через сколько лет первоначальная сумма депозита возрастёт в два раза, если на вложенные средства начисляется 9,75 % годовых и: а) используются простые проценты, б) сложные проценты с полугодовой капитализацией?

Для простых процентов множитель наращения (1 + п * 0,0975) = 2, т.е. п = 10,256 года. При использовании сложных процентов множитель наращивания 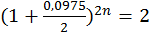, т.е. n=ln2:(2ln(1+ 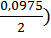)=7,281 года.

Пример 1.2.2. По трёхмесячному депозиту назначена ставка 10,2 % годовых. Какую ставку годовых процентов следует назначить на месячные депозиты, чтобы последовательное переоформление этих депозитов привело бы к такому же результату, что и использование трёхмесячного депозита, если пренебречь двумя днями, которые теряются при переоформлении депозитов (К = 360)?

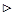Приравняем соответствующие множители наращения: Отсюда получаем, что i =0,101145077 = 10,11%.

1.6. Наращение и инфляция

Наращенная сумма ссуды, депозита с учетом инфляции определяется как

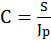где J_p - индекс цен, а S - наращенная сумма, измеренная по номиналу.

Под темпом инфляции понимают относительный прирост цен за период, обозначим его через h. Измеряется темп инфляции в процентах. Между индексом цен j_p и темпом инфляции h существует следующая связь

h = (j_p-1)∙100, j_p= 1 +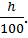

Так как инфляция является цепным процессом, т.е. цены в период t повышаются на h_t процентов относительно уровня, сложившегося в периоде (t – 1), то индекс цен за п таких периодов равен произведению цепных индексов цен:

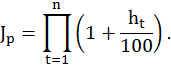
Если наращение по ссуде ведется по ставке простых процентов i, то реальная покупательная способность наращенной суммы S ссуды С равна:

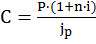где п — срок финансовой операции, а j_p — индекс цен за тот же период. Если наращение ведется по ставке сложных процентов i, то реальная, потребительская ценность наращенной суммы S равна:

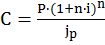Ставку процентов i, которая только компенсирует инфляцию (S = С), обозначим через i*. Если наращение по ccуде длительностью п производится по ставке простых процентов, то .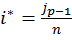

Если же наращение по ссуде производится по ставке сложных процентов , то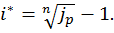

Рис. 8. Изменение множителя наращения с течением времени для сложных процентов с учетом инфляции.

Ставку процентов i, превышающую i*, называют положительной ставкой процентов. Если же i <i*, то ставка i - отрицательная ставка процентов. Для компенсации обесценивания денег, банки увеличивают ставку процентов i на величину так называемой инфляционной премии. Итоговую ставку, которая подавляет инфляцию и обеспечивает прирост реальной денежной массы i в заданном темпе i, обозначим через r. Такую ставку r называют брутто-ставкой (в англоязычной финансовой литературе такую ставку часто называют номинальной ставкой). Если наращение по ссуде длительности п ведется по простым процентам и i -заданный темп роста реальной суммы, то 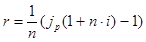если же наращение осуществляется по сложным процентам, то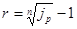

Определим теперь доходность по ссуде с учетом действия инфляции, т.е. так называемую реальную ставку процентов i_p . Если r - объявленная норма доходности по ссуде (брутто-ставка), то, при наращении по простым процентам,

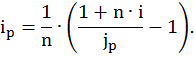
Если же наращение происходит по ставке сложных процентов, то

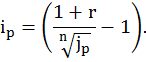
Пример 1.6.1. Ожидается, что в следующие 3 месяца темп инфляции составит соответственно 18, 20 и 21% за каждый месяц. Какую годовую ставку простых процентов следует назначить на трёхмесячный кредит, чтобы реальный прирост денежной массы составил 5% годовых при К = 360?

Индекс цен за 3 месяца j_p = 1,18 • 1,2 • 1,21 = 1,71336. Если r - требуемая годовая ставка простых процентов, которая подавляет инфляцию и обеспечивает рост реальной денежной массы в заданном темпе 5% годовых, то эта ставка должна удовлетворять соотношению (1 + 0,25 • r)/1,71336 = 1 + 0,25 • 0,05. Отсюда имеем r = 2,939108 = 293,9108%.

Пример 1.6.2. Ставка процентов по трёхмесячному депозиту составляет 36% годовых, К = 360. Ожидается, что месячные темпы инфляции составят соответственно 3,1; 3,3 и 3,4%. Какова реальная доходность, в виде годовой ставки простых процентов, инвестирования средств?

Индекс цен за 3 месяца j_p = 1,031 - 1,033 - 1,034 = 1,101233782. Реальная годовая ставка простых процентов j_p должна удовлетворять соотношению: 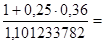1 + 0,25 • i_p. Отсюда получаем: i_p = - 0,040804349 - 4,08%.