При решении задачи надо помнить, что в 5-ой системе счисления самая старшая цифра – 4.

Запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 5:

10 = 20₅, 17 = 32₅ .

Оба они содержат цифру 2, так что, 2 цифры мы уже нашли.

Между 20₅ и 32₅ есть еще числа:

21₅, 22₅, 23₅, 24₅, 30₅, 31₅.

В них 5 цифр 2 (в числе 22₅ – сразу две двойки), поэтому всего цифра 2 встречается 7 раз.

Ответ: 7

 

Решение (вариант 2):

Можно перевести все указанные числа в систему счисления с основанием 5 и подсчитать количество 2:

10 = 20₅, 11 = 21₅, 12 = 22₅, 13 = 23₅, 14 = 24₅, 15 = 30₅, 16 = 31₅, 17 = 32₅ .

Получается 7 штук.

Ответ: 7

 

14. Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.

Решение (вариант 1): Обозначим через неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид:

Любое число в позиционной системе счисления можно представить в виде многочлена по основанию системы счисления:

По условию задачи запись числа трехзначная, т.е. , поэтому:

Из неравенства видно, что подходят только два числа для N – 4 и 5:

Минимальное из этих значений – 4.

Ответ: 4

 

Решение (вариант 2): Так как число по условию трехзначное, то достаточно найти первое целое число, куб которого больше 30; это - 4, так как:

Так как , следовательно, в системе счисления с основанием 4 запись числа 30 трехзначна.

Ответ: 4

 

15. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?

Решение (вариант 1): Сначала определим, сколько цифр может быть в этих числах, записанных в системе счисления с основанием 5. Так как , в интересующих нас числах может быть от 1 до 3 цифр.

Трехзначные числа, начинающиеся на 3 в системе с основанием 5 можно представить:

Все они заведомо не меньше , поэтому в наш диапазон не попадают. Таким образом, остается рассмотреть только однозначные и двухзначные числа. Есть всего одно однозначное число, начинающееся на 3, это 3.

Общий вид всех двузначных чисел, начинающихся на 3 в системе с основанием 5:

,

где 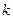– целое число из множества {0, 1, 2,3,4} (поскольку система счисления имеет основание 5 и цифр, больших 4, в записи числа быть не может).

Используя эту формулу, находим интересующие нас двузначные числа – 15, 16, 17, 18 и 19.

Ответ: 3, 15, 16, 17, 18, 19

Решение (вариант 2): Поскольку , в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30). Есть всего одно однозначное число, начинающееся на 3, это 3. Выпишем все пятеричные двузначные числа, которые начинаются с 3, и переведем их в десятичную систему: 30₅ = 15, 31₅ = 16, 32₅ = 17, 33₅ = 18 и 34₅ = 19.

Ответ: 3, 15, 16, 17, 18, 19

 

16. Чему равно наименьшее основание позиционной системы счисления , при котором 225_x = 405_y? Ответ записать в виде целого числа.

Решение: Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с .

Для каждого «подозреваемого» вычисляем значение и решаем уравнение , причем, нас интересуют только натуральные .

Для и нужных решений нет, а для получаем

так что .

Ответ: 8

 

17. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 63₁₀ * 4₁₀ 2) F8₁₆ + 1₁₀ 3) 333₈ 4) 11100111₂

Решение: Нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее из чисел, в которых ровно 6 единиц.

Для первого варианта переведем оба сомножителя в двоичную систему:

63­₁₀ = 111111­₂ 4₁₀ = 100­₂

В первом числе ровно 6 единиц, умножение на второе добавляет в конец два нуля:

63­₁₀ * 4₁₀ = 111111­₂ * 100­₂ = 111111­00₂

то есть в этом числе 6 единиц.

Для второго варианта воспользуемся связью между шестнадцатеричной и двоичной системами счисления: каждую цифру шестнадцатеричного числа можно переводить отдельно в тетраду (4 двоичных цифры):

F­₁₆ = 1111­₂ 8₁₆ = 100­0₂ F8₁₆ = 1111 1000₂

после добавления единицы F8₁₆ + 1 = 1111 1001₂ также получаем число, содержащее ровно 6 единиц, но оно меньше, чем число в первом варианте ответа.

Для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду (группу из трёх) двоичных цифр:

333₈ = 011 011 011­₂ = 11011011₂

это число тоже содержит 6 единиц, но меньше, чем число в первом варианте ответа.

Последнее число 11100111₂ уже записано в двоичной системе, оно тоже содержит ровно 6 единиц, но меньше первого числа

Таким образом, все 4 числа, указанные в вариантах ответов содержат ровно 6 единиц, но наибольшее из них – первое

Ответ: 1

 

18. Даны 4 целых числа, записанные в двоичной системе:
10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем А4₁₆ +20₈?

1) 1 2) 2 3) 3 4) 4

 

Решение: Надо перевести А4₁₆ +20₈ в двоичную систему счисления, разложив их по тетрадам для 16-х чисел и по триадам для 8-х чисел: А4₁₆ - 10100100₂ и 20₈ - 10000₂ и поразрядно сложить: 10100100₂ + 10000₂ = 10110100₂.

Сравнив с заданными числами, видим, что только одно число больше полученного, это: 10111000.

Ответ: 1

 

19. Найти сумму восьмеричных чисел 17₈ +170₈ +1700₈ +...+1700000₈, перевести в 16-ую систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.

Решение: Несложно выполнить прямое сложение восьмеричных чисел, там быстро обнаруживается закономерность:

17₈ + 170₈ = 207₈

17₈ + 170₈ + 1700₈ = 2107₈

17₈ + 170₈ + 1700₈ + 17000₈ = 21107₈

17₈ + 170₈ + 1700₈ + 17000₈ + 170000₈ = 211107₈

17₈ + 170₈ + 1700₈ + 17000₈ + 170000₈ + 1700000₈ = 2111107₈

Переведем последнюю сумму через триады в двоичный код (заменяем каждую восьмеричную цифру на 3 двоичных):

10001001001001000111₂

Теперь разбиваем цепочку на тетрады (группы из 4-х двоичных цифр), начиная справа, и каждую тетраду представляем в виде шестнадцатеричной цифры 89247₁₆

Третья цифра слева: 2.

Ответ: 2

 

20. В системе счисления с некоторым основанием число 17 записывается в виде 122. Укажите это основание.

Решение: Обозначим искомое основание системы счисления через x, тогда можно записать выражение:

17 = x²+2 x+2 или x²+2 x-15 = 0. Решив это уравнение, получим x=3.

Ответ: 3