Линейное (векторное) пространство.
Определение 1.Совокупность nдействительных чисел 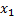 ,
, 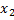 ,…,
,…, 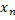 , заданных в определенном порядке, называется n-мерным вектором. Числа
, заданных в определенном порядке, называется n-мерным вектором. Числа 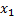 ,
, 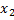 ,…,
,…, 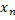 называются координатами вектора.
называются координатами вектора.
Над n-мерными векторами вводятся следующие операции.
Сложение: если x=( 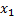 ,
, 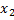 ,…,
,…, 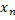 ), y=
), y=  ,
,  ,…,
,…,  ), то x+y=(
), то x+y=( 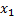 +
+ 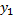 ,
, 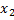 +
+  , … ,
, … , 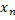 +
+  ).
).
Умножение на число : если 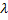 - действительное число и x=(
- действительное число и x=( 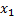 ,
, 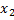 ,…,
,…, 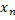 )-вектор, то
)-вектор, то 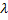 x=(
x=(  ,
, 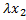 , …,
, …, 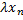 ).
).
Определение 2.Два вектора называются равными, если равны их соответствующие координаты
( 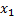 ,
, 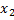 ,…,
,…, 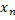 ) =
) =  ,
,  ,…,
,…,  )
) 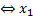 =
= 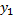 ,
, 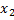 =
=  , … ,
, … , 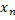 =
=  .
.
Среди n-мерных векторов есть вектор, нейтральный относительно операций сложения.
Этот вектор с нулевыми координатами. Его называют нулевым вектором и обозначают через 0:
0=(0,0,…,0).
Каждый вектор x имеет противоположный : его обозначают –x, причем
-x=(  ,
,  ,…,
,…, 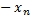 ).
).
Введенные операции сложения векторов и умножение вектора на число обладают восемью свойствами:
1. x+y=y+x
2. (x+y)+z=x+(y+z)
3. x+0=0
4. x+(-x)=0
5. λ(μx)=(λμ)x
6. λ(x+y)= λx+λy
7. (λ+μ)=λx+μx
8. 1·x=x.
Определение 3.Множество всех n-мерных векторов, для которых установлены операции сложения и умножения на число, называется n-мерным векторным (линейным) пространством 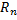
Определение 4.Система n-мерных векторов { 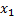 ,
, 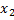 ,…,
,…, 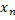 } называется линейно зависимой, если найдутся числа
} называется линейно зависимой, если найдутся числа  ,
, 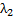 ,…,
,…,  , не равные одновременно нулю, такие, что
, не равные одновременно нулю, такие, что 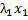 +
+ 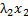 +…+
+…+ 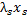 =0.
=0.
В противном случае эта система называется линейно независимой .
Определение 5.Пусть Q- произвольное множество n-мерных векторов пространства 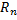 . Система векторов B={
. Система векторов B={  ,
, 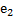 ,…,
,…, 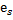 } называется базисом в Q, если выполняются следующие условия:
} называется базисом в Q, если выполняются следующие условия:
1. 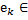 Q, k=1,2,…,s;
Q, k=1,2,…,s;
2. Система B={  ,
, 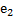 ,…,
,…, 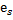 } линейно независима;
} линейно независима;
3. Для любого вектора 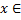 Qнайдутся числа
Qнайдутся числа  ,
, 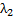 ,…,
,…,  , такие, что x=
, такие, что x= 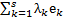 .
.
Определение 6.Формула 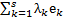 называется разложением вектора xпо базису B=(
называется разложением вектора xпо базису B=(  ,
, 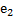 ,…,
,…, 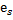 ). Коэффициенты
). Коэффициенты  ,
, 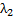 ,…,
,…,  однозначно определяются вектором xи называются координатами этого вектора в базисе В.
однозначно определяются вектором xи называются координатами этого вектора в базисе В.
Справедливы следующие утверждения:
1) Всякая система векторов Q 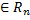 имеет по меньшей мере один базис; при этом все базисы этой системы состоят из одинакового числа векторов, называемого рангом системы Q, и обозначаются r(Q).
имеет по меньшей мере один базис; при этом все базисы этой системы состоят из одинакового числа векторов, называемого рангом системы Q, и обозначаются r(Q).
2) Ранг всего пространства 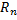 равен n и называется размерностью этого пространства; при этом в качестве базиса
равен n и называется размерностью этого пространства; при этом в качестве базиса 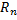 можно взять следующую систему:
можно взять следующую систему:
 Этот базис принято называть каноническим.
Этот базис принято называть каноническим.
Зафиксируем произвольный базис B=(  ,
, 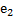 , …,
, …, 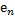 ) в пространстве
) в пространстве 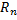 . Тогда всякому вектору x можно поставить взаимно однозначное соответствие столбец его координат в этом базисе, т.е.
. Тогда всякому вектору x можно поставить взаимно однозначное соответствие столбец его координат в этом базисе, т.е.
X= 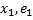 +
+  +…+
+…+ 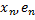 =
= 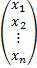 .
.