ДИНАМИКА РОСТА ЧИСЛЕННОСТИ ПОПУЛЯЦИИ
Еще в XVII веке было установлено, что численность популяций растет по закону геометрической прогрессии, а в конце XVIII века Томас Мальтус сформулировал теорию о росте народонаселения в геометрической прогрессии. На современном математическом языке это утверждение выражается экспоненциальным законом роста численности популяций:
 ,
,
где 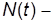 численность популяции в момент времени t;
численность популяции в момент времени t;  численность популяции в начальный момент времени, а постоянная величина r имеет смысл интенсивности размножения особей данной популяции и определяет скорость роста численности популяции с помощью уравнения
численность популяции в начальный момент времени, а постоянная величина r имеет смысл интенсивности размножения особей данной популяции и определяет скорость роста численности популяции с помощью уравнения
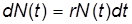 ,
,
согласно которому скорость роста численности популяции пропорциональна самой численности.
Таким образом, экспоненциальный рост численности популяции имеет место, когда величина r постоянна, т.е. представляет собой рост численности популяции в неизменяющихся условиях.
Однако сохранение условий постоянными в течение длительного времени в природе невозможно вследствие существования множества лимитирующих факторов. Поэтому возрастание численности популяции в течение длительного промежутка времени не описывается экспоненциальной зависимостью: экспоненциальный рост обычно наблюдается достаточно короткое время, после чего лимитирующие факторы его стабилизируют. Одной из наиболее простых моделей развития популяции является т.н. логистическая модель, в которой изменение численности популяции описывается логистической кривой роста популяции.
В основе логистической модели лежит простое допущение, что скорость роста популяции r линейно снижается по мере роста численности вплоть до нуля при некоторой максимальной численности K:
 .
.
Тем самым, изменение скорости роста со временем задается зависимостью от времени численности популяции N:
 .
.
Так как по условию  , когда
, когда 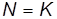 , то из соотношения
, то из соотношения  следует значение углового коэффициента:
следует значение углового коэффициента:  :
:
 .
.
Тогда дифференциальное уравнение для определения временной зависимости численности популяции имеет вид:
 ,
,
или
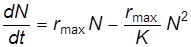 .
.
Умножим это уравнение на  :
:
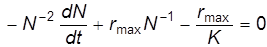 .
.
Обозначим  . Тогда
. Тогда  , и дифференциальное уравнение принимает вид:
, и дифференциальное уравнение принимает вид:
 ,
,
или
 .
.
Обозначая 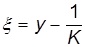 , получаем дифференциальное уравнение
, получаем дифференциальное уравнение
 ,
,
или
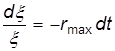 ,
,
решение которого имеет вид
 .
.
Соответственно,  , откуда следует:
, откуда следует:
 ;
;
 ,
,
или  . Обозначим численность популяции в начальный момент времени через N0 = N(0). Из этого начального условия получаем:
. Обозначим численность популяции в начальный момент времени через N0 = N(0). Из этого начального условия получаем:
 ,
,
откуда следует:
 ,
,
или
 .
.
И решение дифференциального уравнения принимает окончательный вид:
 .
.
Согласно последней формуле, рост численности популяции в рамках логистической модели происходит по т.н. S-образной кривой с асимптотическим выходом на плато, когда N = K. Величину K называют также емкостью среды по отношению к особям данной популяции. Речь в данном случае идет о биологической емкости среды - степени способности природного или природно-антропогенного окружения обеспечивать нормальную жизнедеятельность (дыхание, питание, размножение и т.п.) определенному числу организмов без заметного нарушения самого окружения.
Однако плато на S-образной кривой далеко не всегда бывает гладким, потому что постоянно происходят колебания численности популяций, что отражается в виде колебаний кривой около асимптоты N = K. Эти колебания называют флуктуациями численности, которые могут быть сезонными и годовыми. Первые обусловлены абиотическими факторами, вторые также и внутренними, биотическими. Колебания, вызванные биотическими факторами, называют осцилляциями. Типичным примером осцилляций являются колебания численности популяций в системе хищники - жертвы. Рост численности популяции зайцев приводит к несколько запаздывающему росту численности популяции рыси, что снижает потенциальную емкость среды по отношению к зайцам. Поэтому численность популяции зайцев начинает снижаться, что, в свою очередь приводит к снижению численности популяции рыси и т.д.
Стремление к выживанию у различных организмов проявляется по-разному. Соответственно, существует множество различных стратегий выживания. Однако все многообразие экологических стратегий выживания заключено между двумя типами эволюционного отбора, которые обозначаются константами логистического уравнения: r - стратегия и K - стратегия. r - стратегия (r - отбор) направлена, прежде всего, на повышение скорости роста численности популяции и, следовательно, на развитие таких качеств, как высокая плодовитость, ранняя половая зрелость, короткий жизненный цикл, способность быстро распространяться на новые места обитания и переживать неблагоприятное время в стадии покоя. K - стратегия (K - отбор) направлена на повышение выживаемости в условиях уже стабилизировавшейся численности, т.е. на повышение конкурентоспособности, защищенности от хищников и паразитов, повышение вероятности выживания каждого потомка.
Очевидно, что экологические стратегии выживания различных организмов являются теми или иными комбинациями r - отбора и K - отбора, но r - отбор преобладает на ранних стадиях развития популяции, а K - отбор характерен для уже стабилизированных систем. Однако оставляемые отбором особи должны, вообще говоря, обладать и достаточно высокой плодовитостью и достаточно развитой способностью выживания при наличии конкуренции и угнетающего действия хищников.