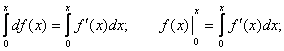Решение систем m линейных неравенств с двумя переменными
Дана система т линейных неравенств с двумя переменными
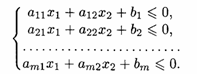
Знаки некоторых или всех неравенств могут быть ≥.
Рассмотрим первое неравенство в системе координат Х1ОХ2. Построим прямую

которая является граничной прямой.
Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).

Полуплоскость 1 содержит начало координат, полуплоскость 2 не содержит начала координат.
Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произвольную точку на плоскости (лучше начало координат) и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.
Направление полуплоскости на рисунках показываем стрелкой.
Определение 15. Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.
Определение 16. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы (ОР).
Определение 17. Область решения системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = ), называется областью неотрицательных, или допустимых, решений (ОДР).
Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной областью или одной точкой.
Если система неравенств несовместна, то ОР и ОДР — пустое множество.
Пример 1. Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР

Решение. Найдем ОР первого неравенства: х1 + 3x2 ≥ 3. Построим граничную прямую х1 +3x2 – 3 = 0 (рис. 19.5). Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (19.1) является полуплоскость, не содержащая точку (0,0).
Аналогично найдем решения остальных неравенств системы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7).
Точку В найдем как точку пересечения прямых

Из системы получим B(5/3, 10/3). Аналогично найдем координаты точек С и D: С(11/4; 9/14), D(3/10; 21/10).
Пример 2. Найти ОР и ОДР системы неравенств

Решение. Построим прямые и определим решения неравенств (19.5)-(19.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 19.6).
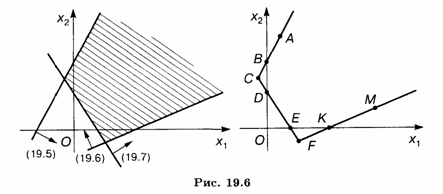
Пример 3. Найти ОР и ОДР системы неравенств

Решение. Найдем решения неравенств (19.8)-(19.10) (рис. 19.7). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.
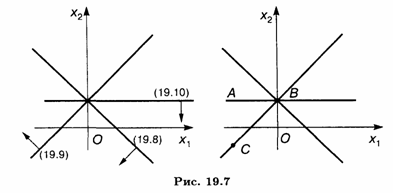
Пример 4. Найти OP и ОДР системы неравенств


Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны (рис. 19.8).
УПРАЖНЕНИЯ
Найти ОР и ОДР систем неравенств
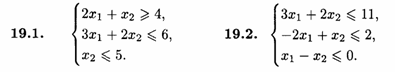

Теорема. Если xn ® a, то  .
.
Доказательство. Из xn ® a следует, что  . В то же время:
. В то же время:
 , т.е.
, т.е.  , т.е.
, т.е.  . Теорема доказана.
. Теорема доказана.
Теорема. Если xn ® a, то последовательность {xn} ограничена.
Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например, последовательность  не имеет предела, хотя
не имеет предела, хотя 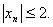
Разложение функций в степенные ряды.
Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.
Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора).
Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей.
Пример. Разложить в ряд функцию  .
.
Суть метода алгебраического деления состоит в применении общего правила деления многочленов.
Если применить к той же функции формулу Маклорена
 ,
,
то получаем: 
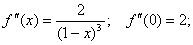
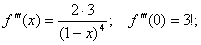
……………………………….

Итого, получаем: 
Рассмотрим способ разложения функции в ряд при помощи интегрирования.
С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.
Находим дифференциал функции  и интегрируем его в пределах от 0 до х.
и интегрируем его в пределах от 0 до х.