Определение разрядности коэффициентов ДЦ

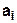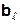Определим разрядность коэффициентов и , если допуск на отклонение системных характеристик составляет 1%.

Важно помнить, что при выборе разрядности умножителей первоначально необходимо задавать ее не меньше чем разрядность АЦП.

Примем разрядность коэффициентов равной 9 (при дальнейших расчетах разрядность коэффициентов может быть изменена в зависимости от полученных результатов).

Представим коэффициенты в виде 9-разрядного двоичного кода. В этом случае разрядная сетка содержит один знаковый разряд и девять числовых. Запятая зафиксирована между знаковым и числовыми разрядами. Значение знакового разряда равно нулю, если коэффициент положителен, и единице в противном случае.

При квантовании чисел различают два вида ошибок:

1. Усечение до разрядов - это отбрасывание младших разрядов.

2. Округление до разрядов - сохранение значения этого разряда или увеличение его на 1 в зависимости от того, больше чем или меньше его отбрасываемая часть.

В дальнейшем будем считать, что при квантовании используется процедура округления.

Для перевода правильной дроби из десятичной системы счисления в двоичную необходимо последовательно умножать данную дробь на 2 (перемножая только дробные части), и выписать последовательно все целые части полученных произведений, начиная с первого. Нам при расчете необходимо получить девять числовых разрядов плюс один дополнительный для выполнения операции округления.

Итак, коэффициенты исходной ДЦ:

Представим каждый из коэффициентов в двоичной системе счисления:

0,7	1,4	0,8	1,6	1,2	0,4	0,8	1,6	1,2	0,4	0,8

 

Восстановление этого коэффициента в десятичной системе:

0,3	0,6	1,2	0,4	0,8	1,6	1,2	0,4	0,8	1,6	1,2

 

Так как дополнительный разряд содержит единицу, произведем процедуру округления:

В десятичной системе:

- 0,1	0,2	0,4	0,8	1,6	1,2	0,4	0,8	1,6	1,2	0,4

 

;

0,5	1.0

 

;

0,2	0,4	0,8	1,6	1,2	0,4	0,8	1,6	1,2	0,4	0,8

 

;

 

Определим относительную погрешность при записи коэффициентов масштабирующих усилителей в 9-и разрядном двоичном коде:

(3.1)

 

Оценка влияния ошибки квантования на импульсную характеристику цепи

 

Импульсная характеристика для передаточной функции исходной ДЦ уже была найдена в разделе 1.3.

Определим импульсную характеристику цепи с коэффициентами, реализованными 9-разрядным двоичным кодом, и рассчитаем относительную погрешность для каждого из отсчетов h(n):

 

(3.2)

 

Расчеты сведем в таблицу:

 

n	h(n)	h/(n)	δh(n), %
	0,7	0,699219	0,112
	0,65	0,650391	0,06
	0,365	0,364883	0,032
	0,3125	0,312011719	0,156
	0,22925	0,22869748	0,241
	0,177125	0,176507324	0,349
	0,1344125	0,13381449	0,445
	0,10263	0,102070812	0,546
	0,078198	0,077693761	0,645
	0,059625	0,0591813	0,745

Таблица 3.1 Импульсная характеристика ДЦ h^/(n)

 

 

Среднеквадратическая ошибка импульсной характеристики составляет:

 

Очевидно, что .

При невыполнении данного условия следует увеличить на 1-2 разряда длину двоичного кода и выполнить все вычисления заново.

 

Оценка влияния ошибки квантования на частотную характеристику цепи

Относительная величина чувствительности к каждому из коэффициентов определяется по формуле

 

(3.3)

и показывает во сколько раз относительное уменьшение передаточной функции цепи больше относительного изменения параметра (коэффициента).

 

(3.4)

 

Наибольшее влияние на АЧХ цепи коэффициент оказывает на частоте, равной собственной частоте нуля или полюса передаточной функции H(z).

Полюсы передаточной функции H(z) были уже найдены в разделе 1.2:

Найдем нули передаточной функции:

 

 

Для определения собственной частоты нуля (полюса) воспользуемся соотношениями:

 

· если , то

· если , то

· если , то

 

Определим чувствительности на каждой из частот:

:

 

 

Погрешности коэффициентов были получены ранее:

 

 

Погрешность АЧХ от неточного задания каждого из коэффициентов составит:

 

Среднеквадратическая погрешность АЧХ цепи составит:

 

 

Аналогичным образом определяем среднеквадратическую погрешность АЧХ на частоте, соответствующей :

 

 

 

Среднеквадратическая погрешность АЧХ цепи составит:

 

 

Итак, исходя из допуска на отклонение системных характеристик (не более 1%), определили разрядность коэффициентов дискретной цепи равной 9.

Если по какой-либо системной характеристике допуск превышен, необходимо увеличить разрядность коэффициентов ДЦ на 1-2 разряда и повторить расчеты.