Конические сечения
Решение второй главной позиционной задачи по 2 алгоритму рассмотрим на примере конических сечений. Ещё в Древней Греции был известен тот факт, что при пересечении конуса различными плоскостями можно получить прямые линии, кривые второго порядка и, как вырожденный случай, точку. На рис. 3-17 показана фронтальная проекция конуса W2, пересечённого фронтально проецирующими плоскостями L2, Г2, F2, D2, S2; в сечениях получаются, соответственно, две прямые а и b, окружность c, эллипс d, парабола m и гипербола k.

Рис. 3-17
Рассмотрим каждый случай получения конических сечений, представленных на рис. 3-17, с точки зрения решения 2 ГПЗ по 2 алгоритму.
1. Две образующие получатся в сечении, если плоскость, пересекая конус, проходит через его вершину (рис. 3-18).
Fkujhbnv^ W Ç L = a?b$ 2 UGP? 2 fku/
- L ^^ G2 Þ a2b2 = L2
- a1b1 Ì W

Рис. 3-18
Частным случаем такого вида пересечения конуса плоскостью является такое положение, при котором плоскость L проходит через ось i конуса (на рис. 3-19 L1 совпадает с плоскостью фронтального меридиана).
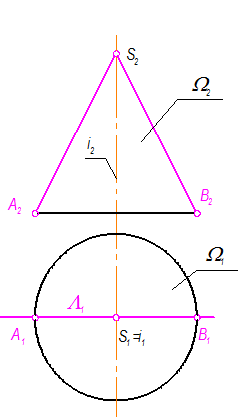
Рис. 3-19
Результатом пересечения являются образующие конуса с максимальным углом между ними (на рис. 3-19 это - очерковые образующие конуса SA и SB).
Алгоритм: W Ç L = SA + SB. 2 ГПЗ, 2 алг.
- L ^^ П1 Þ S1A1 + S1B1 = L1.
- S2A2 + S2B2 Ì W.
2. Окружность получится в сечении, если плоскость, пересекая конус, параллельна окружности основания n (рис 3-20), а значит, перпендикулярна оси i конуса.

Рис. 3-20
Алгоритм: Г Ç W = с. 2 ГПЗ, 2 алгоритм.
- Г ^^ П2 Þ с2 = Г2.
- с1 Ì W .
Вырожденный случай - плоскость Г(Г2) проходит через вершину S конуса W (рис. 3-21). Тогда эта плоскость пересечёт конус только в одной точке. W Ç Г(Г2) = К.

Рис. 3-21
3. Эллипс получится в сечении, если плоскость не перпендикулярна оси конуса и пересекает все его образующие (рис. 3-22, 3-23, 3-24).
Алгоритм: Ф Ç W = d . 2 ГПЗ, 2 алгоритм.
- Ф ^^ П2 Þ d2 = Ф2.
- d1 Ì W.

Рис. 3-22
Построение эллипса начинаем с его осей (рис. 3-22). АВ - большая ось эллипса, причём, А2В2 - её натуральная величина, А1В1 - её проекция. СЕ - малая ось эллипса, она перпендикулярна большой оси и делит её пополам. Чтобы найти СЕ, разделим А2В2 с помощью циркуля пополам, получим точки С2, Е2, и радиусом R , равным радиусу параллели, на которой лежат точки С и Е, сделаем засечки на линии связи, проведённой от точек С2, Е2. Получим точки С1 и Е1. Эти точки - фронтально конкурирующие, С1 - ближе к нам, поэтому Е2 - невидимая.
Далее эллипс можно строить двояко:
1. Можно строить его по двум осям любым из известных способов (например, приведённым в разделе "Кривые линии"). Этот способ показан на рис. 3-23.

Рис. 3-23
2. Можно строить эллипс по точкам, по принадлежности конусу, особенно, если в какой-либо конкретной задаче эллипс получается неполным. Такое решение показано на рис. 3-24.

Рис. 3-24
Построим три проекции линии пересечения конуса с плоскостью Ф. Горизонтальную проекцию точек А, В, С, Е строим так, как показано на рис. 3-22. Остальные, промежуточные, точки строим аналогично точкам С и Е, по принадлежности параллелям конуса. Радиусом параллели, на которой расположена точка, равным расстоянию от оси до очерка конуса, из центра S1делаем засечки на линиях связи от соответствующих точек. Соединяем точки с помощью лекала и получаем горизонтальную проекцию эллипса. При данном расположении конуса эллипс на П1 виден весь.
Построение эллипса на П3 начинаем также с характерных точек. Ими являются:
1) Точки А и В, которые расположены в плоскости фронтального меридиана, следовательно, на П2 - на очерковых образующих, а на П3 - на оси.
2) Точки М и N принадлежат профильным образующим - они определяют видимость эллипса относительно П3: часть эллипса от точки В до точек М и N расположена левее профильных образующих, следовательно, на П3 она видна; соответственно, часть эллипса от точек М и N до точки А на П3 не видна .
3) Промежуточные точки на П3 строим, откладывая координату y для каждой точки (расстояния, помеченные одной, двумя или тремя рисками) с П1 на П3. Соединяем точки с учётом видимости и получаем профильную проекцию эллипса.
4. Парабола получится в сечении, если плоскость, пересекая конус, проходит параллельно только одной его образующей (рис. 3-25).
Алгоритм: W Ç D = m. D || SK. 2 ГПЗ, 2 алгоритм
- ^^ П2 Þ m2 = D2
- m1 Ì W

Рис. 3-25
Построение параболы начинаем с характерных точек:
1) А - вершина параболы. А2 принадлежит очерковой образующей конуса, следовательно, А расположена в плоскости фронтального меридиана Þ А1.
2) Точки В и С - низшие точки параболы, принадлежат окружности основания n конуса, на П1 находим их с помощью линии связи тоже без дополнительных построений.
Промежуточные точки находим так же, как и в случае построения эллипса, то есть по принадлежности параллелям конуса. Соединяем точки с помощью лекала и получаем параболу.
Так как плоскость D параллельна только одной образующей конуса, то парабола имеет одну несобственную точку.
Поэтому, в частном случае, когда плоскость D касается одной образующей SК конуса (рис. 3-26), то получается вырожденный вид параболы - прямая m, совпадающая с SK.

Рис. 3-26
5. Гипербола получится в сечении, если плоскость при пересечении с конусом параллельна одновременно двум образующим конуса (рис. 3-27).
Алгоритм: W Ç S = k. S || SM, S || SN. 2 ГПЗ. 2 алгоритм.
1. S ^^ П2 Þ k2 = S2.
2. k1 Ì W

Рис. 3-27
Построение гиперболы, представленной на рис. 3-27, полностью идентично построению параболы (рис. 3-25).
Так как плоскость S параллельна двум образующим конуса а и b, то гипербола имеет две несобственные точки, и вырожденный вид гиперболы - две прямые а и b (рис. 3-18, 3-19), когда плоскость проходит через вершину конуса.
Рассмотрим частный случай построения гиперболы, когда плоскость S перпендикулярна П1, т.е. является горизонтально проецирующей (рис. 3-28). Построим три проекции линии пересечения конуса W с такой плоскостью S(S1).

Рис. 3-28
Алгоритм: W Ç S = k. S || SO, S || SE, S ^^ П1. 2 ГПЗ 2алгоритм
- S^^ П1 Þ k1 = S1.
- k2 Ì W2
Построение гиперболы начинаем с характерных точек:
Точки М и N принадлежат окружности основания конуса Þ M2,N2 Ì n2. М3 и N3 находим на n3, откладывая координату y этих точек с П1(эти расстояния отмечены двумя и одной риской соответственно).
Точка А располагается в плоскости фронтального меридиана и определяет видимость гиперболы относительно П2: точка N2 - невидимая. А2 лежит на очерковой образующей конуса, а А3 - на оси.
Точка С - вершина гиперболы. Она лежит на перпендикуляре, проведённом от S1 к S1. С2 находим по принадлежности параллели конуса, проведённой через С1. С3 строим аналогично точкам М3 и N3.
Точка В лежит в плоскости профильного меридиана и определяет видимость гиперболы относительно П3. В2 находим по принадлежности параллели, проведённой через В1, В3 лежит на очерковой образующей конуса. Часть гиперболы от В3 до М3 невидимая.
return false">ссылка скрытаПромежуточные точки на П2 находим по принадлежности соответствующим параллелям, аналогично точке С, на П3 - по координатам y этих точек. Соединяем точки с учётом видимости с помощью лекала и получаем фронтальную и профильную проекции гиперболы.
Рассмотрим ещё одну задачу на пересечение поверхностей, из которых одна проецирующая, вторая - непроецирующая.
Задача: Построить линию пересечения сферы S и горизонтально проецирующей призмы Г (рис. 3-29).

Рис. 3-29
Алгоритм: 2 ГПЗ, 2 алг.
1. Вначале определяем, что должно получиться в результате пересечения. Характер пересечения - частный случай вмятия, с одной общей точкой. Призма - трёхгранная, значит можно рассматривать пересечение сферы тремя отдельными плоскостями: D, F и L. Следовательно, линией пересечения является пространственная линия, состоящая из трёх плоских кривых второго порядка: двух дуг эллипсов (S Ç F = a, S Ç L = b) и одной дуги окружности (S Ç D = с).
2. Поскольку поверхность призмы – горизонтально проецирующая, то горизонтальная линия пересечения совпадает с Г1.
3. Фронтальную проекцию линии пересечения сферы с любой из плоскостей, например, Ф, строим по принадлежности сфере. a Ì S Þ а2 Ì S2 (рис. 3-30).
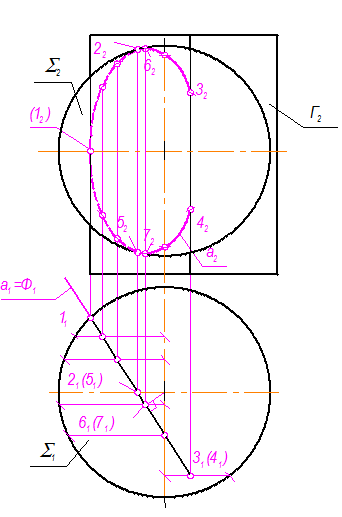
Рис. 3-30
Построения начинаем с характерных точек: 1, 2, 3, 4, 5, 6, 7. Точка 1 принадлежит экватору сферы Þ 12; точки 2 и 5 принадлежат фронтальному меридиану сферы и определяют видимость эллипса а относительно П2 Þ 22 и 52; точки 3 и 4 являются конечными точками дуги эллипса а Þ 32 и 42; точки 6 и 7 - высшая и низшая точки эллипса а. Промежуточные точки, так же, как точки 3, 4, 6, 7, находим по принадлежности параллелям сферы. Проводим а2 с учётом видимости.
4. Аналогично строим линию пересечения сферы с плоскостью L(рис. 3-31): b Ì S Þ b2 Ì S2.

Рис. 3-31
Результат пересечения сферы S с плоскостью D - окружность с (рис. 3-32) расположена за плоскостью фронтального меридиана, следовательно, с2 Ì S2 - невидимая.

Рис. 3-32
На рис. 3-33 показан общий результат решения задачи с учётом видимости поверхностей.

Рис. 3-33
Алгоритм: S Ç Г = а, b, с. Г || П1. 2 ГПЗ, 2 алгоритм.
1. Г ^^ П1 Þ а1, b1, с1 = Г1.
2. а2, b2, с2 Ì S.
Как Вы думаете, верно ли расставлены на П2 номера фигур сечения, соответствующие секущей плоскости S на П1?
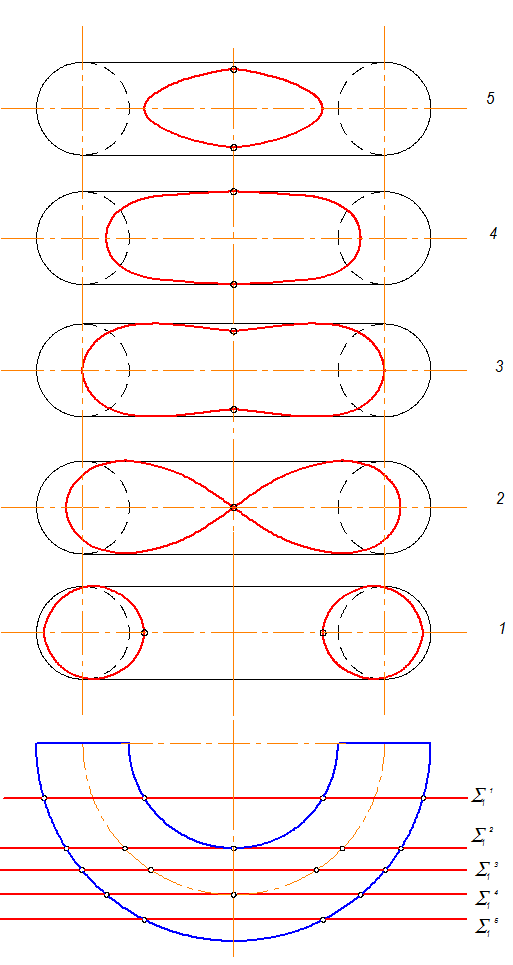
Рис. 3-34