Перечень примерных вопросов к экзамену.

Методика преподавания математики

Группа 4ПОБ_НАЧ-К-В

1. Методика ознакомления со смыслом действий сложения и вычитания, взаимосвязью компонентов и результатов действий сложения и вычитания.

Смысл действий сложения и вычитания. (Власенкова Ю.И.)

В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, вычитание – с операцией дополнения. Этот подход легко интерпретируется на уровне предметных действий, позволяя тем самым учитывать психологические особенности младших школьников. В М1М в качестве основного средства формирования представлений о смысле действий сложения и вычитания выступают простые текстовые задачи.

В основе другого подхода (М1И) лежит выполнение учащимися предметных действий и их интерпретация в виде графических и символических моделей. В качестве основной цели здесь выступает осознание предметного смысла числовых выражений и равенств. Деятельность учащихся сначала сводится к переводу предметных действий на язык математики, а затем к установлению соответствия между различными моделями (под картинкой, где дети выпускают рыбок в один аквариум на писано символическое выражение действия 2+3).

Можно условно выделить три вида ситуаций, связанных с операцией объединения: 1) увеличение данного предметного множества на несколько предметов; 2) увеличение на несколько предметов множества, равночисленного данному; 3) составление одного предметного множества из двух данных.

При формировании у детей представлений о вычитании можно условно ориентироваться на следующие предметные ситуации: 1) уменьшение данного предметного множества на несколько предметов; 2) уменьшение множества, равночисленного данному, на несколько предметов; 3) сравнение двух предметных множеств. В процессе выполнения предметных действий у младших школьников формируется представление о вычитании как о действии, которое связано с уменьшением количества предметов.

(Калинч.) При формировании понятия об арифметических действиях и их свойствах необходимо объяснить смысл сложения, вычитание, умножение, деления, познакомить с компонентами действий, переместительным и сочетательным свойством, показать взаимосвязь сложения и вычитания, умножения и деления.

Сложение имеет следующие компоненты (рис. 34):

Рис. 34

Сложение натуральных чисел выполняется в соответствии с положениями теории множеств и аксиоматической теории.

В теории множеств существует понятие об объединении множеств, которое заключается в том, что при объединении двух множеств, не имеющих общих элементов, получается множество, содержащее элементы этих множеств (рис. 1). В методике на данное положение опирается объяснение смысла сложения как объединение предметов. Предлагаются ситуации, в которых необходимо найти общее количество предметов, узнать, сколько предметов вместе. Например: «У Димы 3 карандаша, а у Севы 2 карандаша. Сколько карандашей у мальчиков?». Также данное положение позволяет выполнять сложение чисел, опираясь на знание состава числа. Например, 5 состоит из 3 и 2, значит, сумма чисел 3 и 2 будет равна 5.

Основная операция над множествами – это установление взаимно-однозначного соответствия между элементами двух сравниваемых множеств. Одно из сравниваемых множеств может быть больше другого на несколько элементов. Такая ситуация также позволяет раскрыть смысл сложения. Например: «У Димы 3 карандаша, а у Севы на 2 карандаша больше. Сколько карандашей у Севы?».

Показать взаимосвязь сложения и вычитания удобнее, рассматривая число как количественную характеристику множества, состоящего из двух подмножеств. Так, множество из 5 геометрических фигур состоит из подмножества трех квадратов и подмножества двух кругов. На примере такого соотношения «часть-целое» в учебнике Л.Г. Петерсон, в учебнике Н.Б. Истоминой[1] объясняется, что при объединении частей (подмножеств) получится целое, а если из целого (данного множества) убрать одну часть (одно подмножество) останется другая часть (другое подмножество). Это наглядно демонстрирует трудные для учащихся правила, необходимые для решения уравнений: чтобы найти уменьшаемое нужно к вычитаемому прибавить разность; чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность; чтобы найти слагаемое, нужно из суммы вычесть другое слагаемое.

Кроме данного подхода в методико-математической литературе сложение рассматривается как увеличение на несколько единиц. Предлагаются ситуации, в которых количество предметов увеличивается, и надо определить, сколько предметов стало, например: «У Лены было 3 заколки, ей подарили еще 2 заколки. Сколько заколок стало у Лены?». Сложение в этом случае выполняется приемом присчитывания по единице, то есть к 3 нужно добавить 2, взять еще четвертую и пятую заколку.

Таким образом, чтобы объяснить учащимся смысл действия сложения целых неотрицательных чисел можно использовать три вида заданий:

а) Составление одного множества из двух данных;

б) Увеличение данного предметного множества на несколько предметов;

в) Увеличение множества, равночисленного данному на несколько предметов.

 

1. Изучение переместительного и сочетательного свойства сложения в начальной школе.

Сложение натуральных чисел обладает свойствами: переместительным свойством (свойство коммутативности) и сочетательным свойством (свойством ассоциативности), доказанными и в теории множеств и в аксиоматической теории.

Переместительное свойство заключается в том, что от перестановки слагаемых значение суммы не меняется, например: 2+1=1+2. Данное свойство изучается в 1 классе, при изучении сложения чисел в пределах первого десятка.

С переместительным свойством можно познакомить школьников следующим образом:

1. Решить пары примеров вида: 3 + 4 и 4 + 3, сравнить, чем похожи и чем отличаются решенные примеры, затем подвести детей к определенному выводу: от перемены слагаемых сумма не изменяется. Аналогично рассматриваются ещё 2 – 3 пары примеров.

2. Можно начать работу с рассмотрения действий с предметными множествами. Приведём вариант примерных рассуждений учителя с учащимися.

- положите 4 больших треугольника и ещё 3 маленьких. Сколько всего треугольников? (7).

- положите 3 красных кружка и 4 зеленых. Сколько всего кружков? (7).

Результат практического действия переводится на язык математики и делаются записи. 4 +3 = 7 и 3 + 4 = 7. Сравниваю записи, выясняют, чем похожи и чем отличаются и делают соответствующие выводы.

Знакомство с новым вычислительным приёмом целесообразно начинать с рассмотрения проблемной ситуации. С решения задачи практического характера: «На одном пришкольном участке дети собрали 2 мешка картофеля, на другом 7. Сколько всего картофеля собрано с двух участков? Необходимо сложить их вместе. Как удобнее, 7 мешков перенести к двум или 2 мешка перенести к семи?». Практическая ситуация переводится на математический язык: 2 +7 или 7 + 2.

Опираясь на жизненную ситуацию и наблюдения, дети убеждаются, что далеко не безразлично как выполнять сложение и выбирают удобный способ.

Сочетательное свойство или правило группировки слагаемых заключается в том, что значение суммы нескольких слагаемых не зависит от порядка, в котором выполняются действия сложения, например: (8+3)+7=8+(3+7). Сочетательное свойство используется для рационального вычисления. Обратим внимание на несколько приемов сложения, в которых применение данного свойства необходимо:

· При сложении однозначных чисел с переходом через разряд. Например, для того, чтобы выполнить сложение, например, 7+5, нужно второе слагаемое представить в виде суммы удобных слагаемых 3+2 и применить сочетательное свойство, то есть изменить порядок сложения: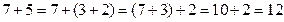

· При выполнении устного сложения чисел в пределах ста (в данном случае используется и сочетательное, и переместительное свойства). Например, чтобы сложить 46+12, нужно представить и первое и второе слагаемое в виде суммы разрядных слагаемых 40+6 и 10+2, далее применить сочетательное свойство, а потом переместительное. Это необходимо, потому что сочетательное свойство можно применить только к рядом стоящим слагаемым: Рассатривая сочетательное свойство Степанова не на теоретичской основе, а на правиле.

Поскольку это очень осложняет объяснение, учащимся сообщается только окончательный результат преобразований и предлагается сначала найти сумму десятков, а потом сумму единиц.

Ознакомление с правилом можно начинать с решения примера: (4+3)+2. Иллюстрация примера: на наборном полотне выкладывают 4 красных больших кружка, 3 синих треугольника и 2 синих кружка (рис.35).

Рис. 35

Предлагается составить примеры: (4 + 3)+2=9, 4 +3 +2=9, 4+(3+2)=9. Сравнив полученные примеры и их результаты, школьники смогут сделать вывод: при сложении трёх слагаемых результат не изменяется, если соседние слагаемые заменить их суммой. Затем по аналогии дети подводятся к правилу: при сложении трёх и более слагаемых соседние числа можно заменить их суммой.

 

1. Изучение правил вычитания числа из суммы и суммы из числа в начальной школе.

В курсе начальной школы не предполагается изучение правил вычитания числа из суммы и вычитания суммы из числа, однако в основе объяснения некоторых приемов вычисления лежат именно эти правила.

Вычитание числа с из суммы a+b предполагает, что число c можно вычесть как из суммы a+b, так и из слагаемого a или b, при условии, если с будет меньше слагаемого, из которого его будут вычитать:

Это правило используется при вычитании разрядных чисел. Уменьшаемое представляется в виде суммы разрядных слагаемых и из нужного разрядного слагаемого вычитается разрядное число. Например, чтобы из 36-2, нужно 36 представить в виде суммы разрядных слагаемых 30+6 и из 6 единиц вычесть 2, прибавить оставшиеся десятки (30). Аналогично можно выполнить вычитание 36-20. Также представить 36 как сумму разрядных слагаемых 30+6 и отнять 20 от десятков, прибавить оставшиеся единицы:

Вычитание суммы b+c из числа a предполагает, что из числа а можно вычесть сумму, а можно каждое слагаемое отдельно:

Это правило используется при вычитании однозначного числа из двузначного с переходом через разряд. Например, чтобы из 16 вычесть 7 можно представить вычитаемое 7 в виде суммы удобных слагаемых 6+1 и отнять от 16 сначала 6, а потом 1:

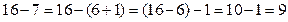
При устном вычитании двузначного числа из двузначного с переходом через разряд. Например, чтобы из 36 вычесть 28, нужно представить вычитаемое 28 в виде суммы разрядных слагаемых 20+8 и вычесть из 36 сначала 20, а потом 8:

Правило вычитание числа из суммы школьники усваивают в процессе выполнения действий с предметными множествами. Например, предлагается школьникам найти значение выражения (5 +4) – 3. Рассматриваются различные способы решения: находят сумму и из полученного результата вычитают число 3; вычитают это число из слагаемого и полученный результат прибавляют к другому слагаемому.

(5 + 4) – 3 = 6; 5 + (4 – 3) = 6; 4 + (5 – 3) = 6.

Сравнивая решение примеров, дети самостоятельно могут сделать вывод: что вычесть число из суммы можно найти сумму и из полученного результата вычесть число, а можно это число вычесть из любого слагаемого и полученный результат прибавить к другому слагаемому.

Для формирования знаний о данном свойстве можно использовать тестовую задачу типа: «Во дворе гуляли 10 девочек и 7 мальчиков. Трое из них ушли домой. Сколько детей осталось?».

Учитель подводит школьников к решению задачи тремя способами, сравнивают решения, устанавливают, чем похожи и чем отличаются решения, а затем делают соответствующие выводы.

Аналогично рассматривается правило вычитания суммы из числа. Это свойство можно продемонстрировать при решении задач. Например, задача: «Оля купила 10 тетрадей. Она отдала подруге 3 тетради в клетку и 1 в линейку. Сколько тетрадей осталось у Оли?». Записывают решения задачи различными способами:

а) 10 – (3 +1) = 6(т.); б) (10 -3) -1 = 6 (т.) в) (10 – 1) – 3 = 6 (т.).

Сравнивая решение задачи (рассматривая различные ситуации над предметными множествами) дети приходят к выводу: сумму из числа можно вычесть тремя способами.

В начальной школе необходимо показать детям зависимость результатов действий от изменения компонентов. Можно провести анализ ряда арифметических примеров

5 + 4 = 9, 5 + 5 = 10, 5 + 6 = 11;

8 + 2 = 10, 7 + 3 = 10, 6 + 4 = 10.

Сравнивая решение примеров, учащиеся подводятся к выводу: если одно из слагаемых увеличить (уменьшить) на несколько единиц, то и сумма увеличится (уменьшится) на столько же единиц.

Кроме этого детям необходимо понять и запомнить, что если одно слагаемое увеличить, а второе уменьшить на столько же единиц, то результат не изменится. Эту закономерность применяют при устных вычислениях. Для этого необходимо предложить учащимся следующие упражнения. Например, зная, что 27 + 3 = 30, определите сумму 27 +5. Рассуждения при выполнении этого задания могут быть примерно следующими: первые слагаемые одинаковые, второе слагаемое на 2 больше, значит и сумма будет больше на 2 единицы. К 30 прибавлю 2, получится 32. Записываю решение: 27 + 5 = 32.

Изучается изменение результата в зависимости от изменения компонентов действия вычитания. Однако это требует проведение большего количества тренировочных упражнений, так как этот материал вызывает у учащихся большие затруднения. Например, если на несколько единиц увеличить уменьшаемое, то и разность будет больше на столько же единиц. Если на несколько единиц увеличить вычитаемое, то разность будет меньше на столько же единиц. Если одновременно увеличить и уменьшаемое и вычитаемое на одинаковое количество единиц, то разность не изменится.

7. Решите задачу: «Из пункта А в одном направлении вышли одновременно два пешехода. Скорость первого 7 км/ч, а скорость второго 5 км/ч. Какое расстояние будет между ними через 3 часа после выхода?» двумя арифметическими способами. Укажите, какие связи и зависимости в ней рассматриваются? Проведите работу на этапе поиска решения задачи.

 

8. Выполните наглядную интерпретацию задачи, приведите её решение и укажите, какие величины и отношения между ними рассматриваются в задаче: «Сад прямоугольной формы равен 400 м². Найти длину изгороди сада, если длина его равна 80м»..

 

* забыла "?" поставить на рисунке((

 

 

9. Решите задачу. Объясните методику составления плана решения. «Имеется два сосуда вместимостью 5 л и 3 л. Как с их помощью налить из водопроводного крана 4 литра воды?»