СПЕЦИФИЧЕСКОЕ РАСЩЕПЛЕНИЕ ДНК УЛЬТРАЗВУКОМ
Чтобы выяснить, влияет ли на относительную частоту расщепления не только тип динуклеотида (фактор A), но и какой вклад в общую изменчивость относительной частоты расщепления обусловлен последовательностью анализируемого участка рестриктного фрагмента ДНК (фактор B), будем использовать двухфакторный дисперсионный анализ. Уровни фактора A являются постоянными, а уровни фактора B естественно рассматривать как случайные. В этом случае для анализа результатов эксперимента используется смешанная двухфакторная модель. В качестве плана эксперимента рассмотрим двухфакторный план с группировкой (nested design) для смешанной модели. Это план, для которого уровни одного фактора A группируются по уровням другого фактора B. При этом каждый уровень фактора В группируется не более чем с одним уровнем фактора A, и фактор B называется сгруппированным фактором A, B(A). Такой план позволяет оценить и ошибки наблюдения, и вклад случайного фактора B(A) в общую изменчивость относительной частоты расщепления, и влияние постоянного фактора A на относительную частоту расщепления.
Для построения такого плана для каждого типа динуклеотида (постоянный фактор A с I уровнями) случайно выбирались «свои» J фрагментов ДНК (случайный фактор B с J уровнями). У каждого из J фрагментов для типа динуклеотида NN определяли значения частоты расщепления этого динуклеотида NN. В этом случае каждый уровень фактора B сочетался не более чем с одним уровнем фактора A.
Смешанная модель для двухфакторного плана с группировкой имеет вид
yijk = μ + αi + bj(i) + εijk, k=1,…, kij, i=1,…, I; j=1,…, J,
где μ – общее среднее, αi – эффект i-огоуровня постоянного фактора A, bj(i) – эффект j-огоуровня случайного фактора B, B(A), сгруппированного i-ым уровнем фактора A;  – неизвестные параметры; εijk – ошибки наблюдений; bj(i) и εijk – независимые в совокупности случайные величины с нулевым средним и дисперсиями
– неизвестные параметры; εijk – ошибки наблюдений; bj(i) и εijk – независимые в совокупности случайные величины с нулевым средним и дисперсиями 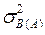 и
и  , соответственно. Дисперсия наблюдения yijk будет равна
, соответственно. Дисперсия наблюдения yijk будет равна 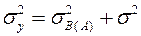 . Компонента дисперсии
. Компонента дисперсии 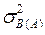 обусловлена вкладом случайного фактора B(A), сгруппированного фактором A, в общую изменчивость зависимой переменной.
обусловлена вкладом случайного фактора B(A), сгруппированного фактором A, в общую изменчивость зависимой переменной.
Было рассмотрено пять моделей такого типа, и построено пять планов с группировкой для каждой из них:
1. Для анализа частоты расщепления каждого из 16 динуклеотидов ДНК, NN; I=16; J=8.
2. Для анализа частоты расщепления каждого из динуклеотидов ДНК, AN; I=4; J=19.
3. Для анализа частоты расщепления каждого из динуклеотидов ДНК, СN; I=4; J=19.
4. Для анализа частоты расщепления каждого из динуклеотидов ДНК, GN; I=4; J=23.
5. Для анализа частоты расщепления каждого из динуклеотидов ДНК, TN; I=4; J=19.
Статистические задачи дисперсионного анализа для рассматриваемой модели состоят в том, чтобы найти оценки неизвестных параметров и проверить статистические гипотезы. Для такой модели проверяются две гипотезы:
Статистические задачи дисперсионного анализа для рассматриваемой модели состоят в том, чтобы найти оценки неизвестных параметров и проверить статистические гипотезы. Для такой модели проверяются две гипотезы:
1. H0: все αi=0, i=1,..., I, что означает – фактор A не влияет, при альтернативе, что, по крайней мере, αk ≠0, что означает – фактор A влияет.
2. H0: 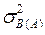 =0 о том, что фактор B(A) не вносит никакого вклада в дисперсию наблюдений, при альтернативе H1:
=0 о том, что фактор B(A) не вносит никакого вклада в дисперсию наблюдений, при альтернативе H1: 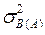 ≠0.
≠0.
Необходимо отметить, что все построенные планы являются планами с неравным числом наблюдений при разных комбинациях уровней факторов A и B(A). Поэтому при определении значений числа степеней свободы, ν*, которые в таблицах не приводятся, оценок компонент дисперсии, значений MS, и, следовательно, наблюденного значения статистики критерия, F-отношения, использовался метод Саттервейта. В табл. 7 приведены значения оценок компонент дисперсии и оценка доли дисперсии наблюдения, которая обусловлена фактором B(A) для каждой из пяти рассматриваемых моделей. Оценка дисперсии единичного наблюдения,  , определялась как сумма оценок компонент дисперсии
, определялась как сумма оценок компонент дисперсии  и
и 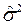 .
.
Таблица 2. Результаты дисперсионного анализа
для динуклотидов NN.
| Источник разброса | Число степеней свободы ν | Средний квадрат MS | F-отношение | p- Значение |
| фактор A | 2,41 | 24,82 | 0,00 | |
| фактор B(A) | 0,09 | 2,21 | 0,00 | |
| Остаток | 0,04 |
Анализ табл. 2 показывает, что влияние типа динуклеотида NN и первичной структуры фрагмента ДНК на относительную частоту ультразвукового расщепления статистически значимо на уровне α=0,05
Таблица 7. Значения оценок компонент дисперсии. Обозначения:  /
/  – оценка доли общей дисперсии, обусловленной фактором B(A);
– оценка доли общей дисперсии, обусловленной фактором B(A); 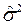 /
/  – оценка доли дисперсии ошибки наблюдения.
– оценка доли дисперсии ошибки наблюдения.
| Модель | 
| 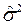
| 
|  / /  *100%
*100%
| 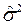 / /  *100%
*100%
|
| 0,0038 | 0,0357 | 0.0395 | 9,6% | 90,4 | |
| 0,0034 | 0,0256 | 0,0290 | 11,7% | 88,3 | |
| 0,0096 | 0,0976 | 0,1072 | 9,8% | 90,2 | |
| 0,0050 | 0,0379 | 0,0429 | 11,6% | 88,4 | |
| 0,0011 | 0,0208 | 0,0219 | 5,0% | 95,0 |
Статистический анализ экспериментальных данных расщепления ДНК ультразвуком выявил влияние на относительную частоту расщепления двух факторов, типа динуклеотида и нуклеотидной последовательности фрагмента ДНК, и позволил оценить долю дисперсии наблюдения, которая обусловлена случайным фактором – нуклеотидной последовательностью фрагмента ДНК. Результаты анализа показали, что вклад случайного фактора в общую изменчивость относительной частоты расщепления, много меньше, чем вклад фактора – тип динуклеотида.