Е с к е р т у

Егер (1) теңдеудің оң жағы (3) түрде болмаса, онда (1) теңдеудің жалпы шешімін тұрақтыны вариациялау әдісімен табамыз.

Мысал 1. теңдеудің жалпы шешімін табу керек.

Мысал 2. теңдеудің жалпы шешімін табу керек.

Мысал 3. теңдеудің жалпы шешімін табу керек.

Мысал 4. теңдеудің жалпы шешімін табу керек

Өзін-өзі бақылауға арналған тестілер:

1.Теңдеуді шешіңіз:

[a]

2. дифференциалдықтеңдеуініңретітең

[a] 2

[a] 1

[a] 0

[a] 3

[a] 4

3.2-шіреттідифференциалдықтеңдеудішешіңіз

[a]

4.– шіреттідифференциалдықтеңдеудішешіңіз

[a]

5.Екінші ретті тұрақты коэффициентті сызықтық біртекті теңдеудің фундаментальды

Шешімдер жүйесінің және сипаттамалық теңдеудің әртүрлі түбірлері болған

жағдайда берілуі:

[a]

7. теңдеуінің мінездемелік теңдеуін құрыңыз:

[a]

8. теңдеуінің мінездемелік теңдеуін құрыңыз:

[a]

[a] \

9.Дифференциалдық теңдеудің жалпы шешімін табыңыз:

[a]

10.Теңдеудің дербес шешімдерін табыңыз:

[a]

[a][+]

[a]

14-ші дәріс

Сандық қатарлар

1. Сандық қатарлар.

2. Таңбасы оң қатарлар.

3. Таңбалары ауыспалы қатар.

1. Сандық қатарлар

Анықтама 1. Берілген шектеусіз сандар тізбегі үшін:

(1)

өрнегі сандық қатар деп аталады, мұндағы - сандары қатардың мүшелері, ал сан қатардың бөлік қосындысы деп аталады.

Анықтама 2. Егер шегі табылатын болса, онда (1) қатарының қосындысы деп аталады.

Анықтама 3. Қатар жинақты деп аталады, егер тұрақты санға тең болса, кері жағдайда, яғни, шегі шексіздікке тең болса немесе табылмаса, онда қатар жинақсыз деп аталады.

Мысал 1. Қатардың қосындысын тап:

Шешуі: Қатардың жалпы мүшесі: .

Алынған формуланы қолданып, қатардың -ші бөлік қосындысын табайық:

Сонымен,

Ендеше, берілген қатар жинақты және оның қосындысы .

Мысал 2. түріндегі қатарды (геометриялық прогрессия) қарастырайық. Онда бөлік қосынды:

1) Егер

2) Егер табылмайды.

3) Егер

а) ( болса)

б) , егер жұп болса және , егер 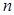тақ болса,

табылмайды.

Сонымен, қатар болғанда ғана жинақты.

Қатардың соңғы мүшелерін лақтырып тастағаннан оның жинақтылығы өзгермейді. Жинақты қатар:

үшін келесі теңдік орынды:

а)

б)

Қатардың жинақтылығының қажетті шарты. (1) қатары жинақты болуы үшін болуы қажетті.

Мысал 3. қатары жинақсыз, себебі қатардың жинақты-лығының қажетті шарты орындалмайды: . болу шартынан қатардың жинақты екені шықпайды.

1.1 Таңбасы оң қатарлар

2-ші мысалда көрсетілгендей бөлік қосындысының ақырлы формуласын анықтау кей жағдайларда қиындық туғызуы мүмкін. Сондықтан, қатардың жалпы мүшесін білу ғана жеткілікті болатын қатардың жинақтылығының жеткілікті белгілерін білген жөн. Тек қана таңбалары оң қатарлар үшін ғана ақиқат болатын белгілерге тоқталайық.

Мүшелері оң сандар болатын қатарларды қарастырамыз:

(2)

(3)

Салыстыру белгілері:

Егер қандай да бір нөмірінен бастап, теңсіздігі орынды болса, онда

а) (3) қатарының жинақтылығынан (2) қатарының жинақты екені шығады;

б) (2) қатарының жинақсыздығынан (3) қатарының жинақсыз екені шығады.

2. Егер ақырлы шегі табылса, онда (1) және (2) қатарлары не екеуі де бірдей жинақты, не екеуі де бірдей жинақсыз.

Мысал 4. Қатарды жинақтылыққа зертте:

(4)

Жинақты (1 мысал, ) болатын

қатарын қарастыралық, үшін: болғандықтан, ендеше (4) қатары жинақты.

Даламбер белгісі (Коши). Егер , мұндағы ақырлы сан болса, онда:

а) егер болса, онда (1) қатары жинақты,

б) егер болса, онда (1) қатары жинақсыз,

в) қатардың жинақтылығы туралы сұрақ ашық қалады.

Мысал 5. Қатарды жинақтылыққа зерттеңіз: а)

, яғни, жинақтылықтың қажетті шарты орындалады. Коши белгісін қолданамыз: қатар жинақты.

б) гармоникалық қатар үшін:

Жинақтылықтың қажетті шарты: орындалады. Даламбер белгісін қолдана-мыз: жинақтылық туралы сұрақ ашық қалады.

Мысал 6. .

Шешуі: болады. Коши белгісін қолдансақ:

Яғни, берілген қатар жинақты.

Кошидің интегралдық белгісі. Қандай да бір нөмірінен теңсіздігі орындалсын және функциясы мынадай үзіліссіз өспелі емес функция болсын: . Онда егер жинақты (жинақсыз) болса, онда (1) қатары жинақты (жинақсыз).

Мысал 7. Берілген қатарды жинақтылыққа зертте:

, . (5)

қатардың жинақтылығының қажетті шарты орындалады.

болғандықтан, деп алып, Кошидің интегралдық белгісін қолдансақ:

а) болса, онда , яғни, интеграл жинақсыз.

б) .

Бұл интеграл болғанда жинақты, ал жинақсыз. Ендеше, (5) қатары болғанда ғана жинақты, ал қалған жағдайларда жинақсыз. Егер болса, (5) қатары біз жоғарыда 5-мысалда қарастырған гармоникалық қатар болады және ол жинақсыз. Ал болса, онда (5) Дирихле қатары деп аталады.

Мысал 8. Қатарды жинақтылыққа зертте: .

Шешуі: қатарымен салыстыралық, бұл қатар көрсеткіші болатын Дирихле қатары және ол жинақсыз. . Ендеше, салыстырудың бірінші белгісі бойынша берілген қатар жинақсыз.

1.2 Таңбалары ауыспалы қатар

, (6)

, (7)

қатарларын қарастырамыз.

Анықтама 4. (6) сандық қатарының мүшелері деп аталатын оң да, теріс те болатын болса, онда бұл қатар таңбалары ауыспалы қатар деп аталады.

Таңбалары алма-кезек ауыспалы қатар (6) қатарының дербес жағдайы:

(8)

Лейбниц белгісі. Егер (8) қатарының мүшелері үшін қандай да бір нөмірінен бастап теңсіздігі орындалып және болса, онда (8) қатары жинақты және оның қосындысы оң сан.

Теорема 1. Егер (7) қатары жинақты болса, онда (6) қатары да жинақты.

Егер (6) қатары жинақты болып, ал (7) қатары жинақсыз болса, онда (6) қатары шартты жинақты деп аталады. Егер (7) қатары жинақты болып және сонымен қатар, (6) қатары да жинақты болса, онда (6) қатары абсолютті жинақты деп аталады. (6) таңбалары ауыспалы қатардың жинақтылығы туралы сұрақ, жалпы жағдайда, таңбалары оң қатар (7)-нің жинақтылығымен шешіледі. Ал таңбалары оң қатардың жинақтылық белгілерін жоғарыда қарастырдық.

Мысал 9. (9)

Қатары Лейбниц белгісі бойынша жинақты, ал оның абсолют шамаларынан құрылған қатар (гармоникалық қатар) жинақсыз. Ендеше, (9) қатары шартты жинақты.

Мысал 10. .

Шешуі: Берілген қатардың абсолют шамаларынан құралған қатарды қарастырамыз: .

Бұл қатар Коши белгісі бойынша жинақты: .

Сонымен, берілген қатар абсолютті жинақты.

Мысал 11. .

Шешуі: Берілген қатардың абсолют шамаларынан құралған қатарды қарастырамыз: , бұл қатар көрсеткіші болатын Дирихле қатары.

Берілген қатар таңбасы алма-кезек ауыспалы қатар болғандықтан, Лейбниц белгісін қолдансақ:

1) , яғни, қатардың мүшелерінің тізбегі кемімелі;

2) .

Ендеше, берілген қатар шартты жинақты.

Өзін-өзі бақылауға арналған тестілер:

1. қатарды жинақтылыққа зерттеңіз

[a] Жинақты

[a] Жинақсыз

[a]Ештеңе айта алмаймыз

[a]Қосындысы шексіздікке тең

[a]Шартты жинақты

2. қатарды жинақтылыққа зерттеңіз

[a] Жинақты

[a] Жинақсыз

[a] Ештеңе айта алмаймыз

[a] Шартты жинақты

[a] Қосындысы жоқ

3.Төменде берілген қатардың жинақтылығын зерттеңіз .

[a] Жинақты

[a]Жинақсыз

[a]Қосындысы жоқ

[a]Бұл гармониялық қатар

[a]Қосындысы жоқ

4.Мына қатардың жинақтылық облысын табыңыз

[a] Бүкіл жазықтықта жинақты

[a] (-1,1) облысындажинақсыз

[a] (-1,1)

[a] (0,2)

[a] (-2,2)

5.Қатардың жалпы мүшесін табыңыз:

[a]

6.Қатардың жалпы мүшесін табыңыз:

[a]

7.Қатардың жалпы мүшесін табыңыз:

[a]

8.Қатардың жалпы мүшесін табыңыз:

[a]

15-ші дәріс

Функционалдық қатарлар. Дәрежелік қатар. Функцияны дәрежелік қатарға жіктеу

1. Функционалдық қатарлар.

Анықтама 1. Функционалдық қатар деп:

(1)

мұндағы қатардың мүшелері функциялар болатын қатарды айтамыз.

-ке қандай да бір тұрақты мән берсек, (1) қатары сандық қатарға айналады. Сонымен, -тің қандай да бір мәндерінде (1) қатары жинақты, қандай да бір мәндерінде жинақсыз.

Анықтама 2. (1) қатары жинақты болатын мәндер жиыны функционалдық қатардың жинақтылық облысы деп аталады.

Қатардың жинақтылық облысында қатардың қосындысы -ке байланысты функция болатындықтан, қатардың қосындысын деп белгілейміз.

Мысал 1. болған жағдайда, қатары жинақты. Себебі, бұл қатар кемімелі геометриялық прогрессия ( ) және оның қосындысы Сонымен, (-1,1) интервалында берілген қатар жинақты және

қатардың қалдық мүшесі.

Теорема 1. (1) қатарының жинақтылық облысында:

2. Бірқалыпты жинақтылық. Функционалдық қатарларға қолданылатын амалдар.

Анықтама 3. (1) қатары облысында мажорланған деп аталады, егер үшін:

теңсіздігі орындалатындай,

, (11)

таңбалары оң жинақты сандық қатар табылса.

Мысал 2.

қатары барлық сан өсінде мажорланған екені анық, өйткені, , а ряд - қатары жинақты қатар (мысал 5).

облысында мажорланған қатар, осы облысында абсолютті жинақты.

Анықтама 4. аралығында жинақты (1) қатары бірқалыпты жинақты деп аталады, егер барлық үшін

болса.

Теорема 2. аралығында мажорланған (1) қатары осы кесіндіде бірқалыпты жинақты.

2-теоремадан мажорланған қатар болу бірқалыпты жинақтылықтан да күшті шарт екенін көреміз, яғни, бірқалыпты жинақтылықтан, бірақ мажорланған емес қатарлар табылады.

Теорема 3. (1) қатары аралығында бірқалыпты жинақты және оның қосындысы болсын. Онда егер:

1. - табылса, онда

2. қатардың мүшелері аралығында үзіліссіз және функциясы да

аралығында үзіліссіз болса, онда

, яғни,

қатарды мүшелеп интегралдауға болады.

Теорема 4. Егер (1) қатары аралығында жинақты болса, , ал қатары аралығында бірқалыпты жинақты болса, онда

яғни, қатарды мүшелеп дифференциалдауға болады.

3. Дәрежелік қатарлар.

Анықтама 5. -ға қатысты дәрежелік қатар деп:

(3)

түрінде берілген қатарды айтамыз, мұндағы коэффициенттері тұрақты сандар. Егер болса, онда: . (4)

Теорема 4. (Абель). болғанда (4) қатары жинақты болса, онда ол болғанда абсолютті жинақты, ал оның болғанда жинақсыз болуынан, болғанда жинақсыздығы шығады.

Абель теоремасынан: (4) қатары үшін жалғыз ғана саны, , табылады, болғанда (2) қатары жинақты, ал үшін жинақсыз болатындай.

саны дәрежелік қатардың жинақтылық радиусы деп аталады, ал жинақтылық интервалы деп аталады. Егер ақырлы шегі табылса, онда қатарына Даламбер белгісін қолдансақ, , яғни, .

Дәл осылай, Коши белгісін қолдансақ: .

Мысал 3. қатарының жинақтылық облысын тап.

болғандықтан, жинақтылық радиусы. нүктелерінде жинақтылыққа зерттейміз.

- гармоникалық қатар жинақсыз болады.

таңбасы алма-кезек ауыспалы қатар, жинақты қатар (мысал 6). Сонымен, берілген дәрежелік қатардың жинақтылық облысы: .

(3) қатарының жинақтылық интервалы , мұндағы (4) қатарының жинақтылық радиусы.

кез келген бүтіндей (3) қатарының жинақтылық интервалының ішінде жататын кесінді болсын. Онда:

1. (3) қатары мажорланған (бірқалыпты жинақты) кесіндісінде.

2. (3) қатарының қосындысы жинақтылық интервалында үзіліссіз.

3. (3) қатарын кесіндісінде мүшелеп интегралдауға және қанша болса сонша рет мүшелеп дифференциалдауға болады, сонымен қатар, алынған дәрежелік қатардың жинақтылық интервалы (3) қатарының жинақтылық интервалымен бірдей.

4. Тейлор қатары

функциясының қандай да бір нүктесінің аймағында -ші ретті туындысы бар болсын. Дәрежесі 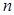-нан жоғары емес төмендегі теңдік орындалатын көпмүшелігін табалық:

(5)

көпмүшелігін мына түрде іздейміз:

-ті тауып (5) шартын қолдансақ:

қалдық мүшесі болсын. Онда және -ті Лагранж формуласында жазуға болатынын көрсетуге болады:

(6)

(6) формуласы Тейлор формуласы деп аталады, ал болса, Маклорен формуласы деп аталады.

Бұл формулалар функциясын көпмүшелігімен -ға тең дәлдікте айырбастауға мүмкіндік береді.

Мысал 4. функциясын Маклорен формуласы бойынша жікте және санын дәлдікке дейін есепте.

болса, . үшін , ал

үшін: болғандықтан, . Сонымен, .

нүктесінің аймағында функциясы шексіз рет дифференциалданатын болсын. Онда -ді өте үлкен шама деп ала отырып, (4) теңдігінің оң жағында дәрежелік функция аламыз. Қандай шарт орындалғанда бұл қатардың қосындысы тең?