Движение напорных вод к совершенной вертикальной дрене

На рис.8 показана совершенная вертикальная дрена круглого сечения радиусом r. Совершенная дрена вскрывает водоносный пласт на всю его мощность и имеет в пределах его проницаемые стенки. Динамический уровень воды в ней при установившемся притоке соответствует напору h, напор на границе депрессионной воронки равен Н, а ее радиус R. Мощность пласта и его коэффициент фильтрации постоянны и равны соответственно m и k_ф.

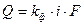Расположив координатные оси по оси выработки и по нижнему водоупору, рассмотрим цилиндрическое сечение Y на расстоянии х от начала координат, площадь которого равна . Расход Q потока подземных вод к выработке через это сечение согласно выражается , где - напорный градиент в сечении.

 

 

 

Рис. 8. Схема движения напорных вод к совершенной вертикальной дрене

 

Разделяя переменные и интегрируя это уравнение , получим или с учетом получим . Подставив значение p и заменив натуральные логарифмы на десятичные, получим . Из данной формулы видно, что дебит совершенной горной выработки прямо пропорционален коэффициенту фильтрации пласта, его мощности и понижению уровня воды и обратно пропорционален логарифму отношения . Величины R и r, входящие в формулу под знаком логарифма, даже при значительных их изменениях существенного влияния на дебит не оказывают.

Уравнение депрессионной кривой имеет вид:

.

Данные для выполнения расчетов:

k_ф = 12 м/сутки - коэффициент фильтрации;

m = 6 м - мощность водоносного пласта;

S – понижение (эта величина задается исходя из условий осушения будущих горных выработок);

r = 1 м – радиус выработки;

- радиус влияния дрены, м, где - коэффициент уровнепроводности, м²/сут;

t = 1 год = 365 суток, время для которого определяется радиус влияния

Для построения кривой принять х₁=0,1R; х₂=0,15R; х₃=0,2R; х₄=0,3R; х₅=0,5R; х₆=0,8 R.