Теплоёмкость

Известно, что подвод теплоты к рабочему телу в каком-либо процессе сопровождается изменением температуры. Отношение теплоты, подведённой (отведённой) в данном процессе, к изменению температуры называется теплоёмкостью тела.

,

где dQ – элементарное количество теплоты

dT – элементарное изменение температуры.

Теплоёмкость численно равна количеству теплоты, которое необходимо подвести к системе, чтобы при заданных условиях повысить температуру на 1 градус. Измеряется в [Дж/К].

Количество теплоты, подведённое к рабочему телу, всегда пропорционально количеству рабочего тела. Например, количество теплоты, необходимое для нагревания на 1 градус кирпича и кирпичной стены неодинаково, поэтому для сравнения вводят удельные величины теплоёмкости, отнеся подведённую теплоту к единице рабочего тела. В зависимости от количественной единицы тела, к которому подводится теплота в термодинамике, различают массовую, объёмную и мольную теплоёмкости.

Массовая теплоёмкость – это теплоёмкость, отнесённая к единице массы рабочего тела,

.

Количество теплоты, необходимое для нагревания 1 кг газа на 1 К называется массовой теплоёмкостью.

Единицей измерения массовой теплоёмкости является Дж/(кг К). Массовую теплоёмкость называют также удельной теплоёмкостью.

Объёмная теплоёмкость – теплоёмкость, отнесённая к единице объёма рабочего тела,

.

Количество теплоты, необходимое для нагревания 1 м³ газа на 1 К называется объёмной теплоёмкостью.

Объёмная теплоёмкость измеряется в Дж/(м³ К).

Мольная теплоёмкость – теплоёмкость, отнесённая к количеству рабочего тела,

,

где n – количество газа в моль.

Количество теплоты, необходимое для нагревания 1 моль газа на 1 К называется мольной теплоёмкостью.

Мольную теплоёмкость измеряют в Дж/(моль×К).

 

Массовая и мольная теплоёмкости связаны следующим соотношением:

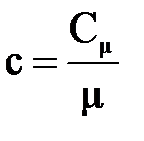или С_m = mс, где m - молярная масса

 

Теплоёмкость зависит от условий протекания процесса. Поэтому обычно в выражении для теплоёмкости указывается индекс х, который характеризует вид процесса теплообмена.

.

Индекс х означает, что процесс подвода (или отвода) теплоты идёт при постоянном значении какого-либо параметра, например, давления, объёма.

Среди таких процессов наибольший интерес представляют два: один при постоянном объёме газа, другой при постоянном давлении. В соответствии с этим различают теплоёмкости при постоянном объёме C_v и теплоёмкость при постоянном давлении C_p.

1) Теплоёмкость при постоянном объёме равна отношению количества теплоты dQ к изменению температуры dT тела в изохорном процессе (V = const):

;

2) Теплоёмкость при постоянном давлении равна отношению количества теплоты dQ к изменению температуры dT тела в изобарном процессе (Р = const):

Для понимания сути этих процессов рассмотрим пример.

Пусть имеется два цилиндра, в которых находится по 1 кг одного и того же газа при одинаковой температуре. Один цилиндр полностью закрыт (V = const), другой цилиндр сверху закрыт поршнем, который оказывает на газ постоянное давление Р (P = const).

Подведём к каждому цилиндру такое количество тепла Q, чтобы температура газа в них повысилась от Т₁ до Т₂ на 1К. В первом цилиндре газ не совершил работу расширения, т.е. количество подведённого тепла будет равно

Q_v = c_v (T₂ – T₁) ,

здесь индекс v – означает, что теплота подводится к газу в процессе с постоянным объёмом.

Во втором цилиндре, кроме повышения температуры на 1К, произошло ещё передвижение нагруженного поршня (газ изменил объём), т.е. была совершена работа расширения. Количество подведённого тепла в этом случае определится из выражения:

Q_р = c_р (T₂ – T₁)

Здесь индекс р – означает, что тепло подводится к газу в процессе с постоянным давлением.

Общее количество тепла Q_p будет больше Q_v на величину, соответствующую работе преодоления внешних сил:

Q_p – Q_v = R,

где R – работа расширения 1 кг газа при повышении температуры на 1К при Т₂ – Т₁ = 1К.

Отсюда С_р – С_v = R

Если поместить в цилиндр не 1 кг газа, а 1 моль, то выражение примет вид

Сm_Р - Сm_v = R_m , где

R_m - универсальная газовая постоянная.

Это выражение носит название уравнения Майера.

Наряду с разностью С_р – С_v в термодинамических исследованиях и практических расчетах широкое применение имеет отношение теплоемкостей С_р и С_v, которое называется показателем адиабаты.

k = С_р / С_v.

В молекулярно – кинетической теории для определения k приводится следующая формула k = 1+2/n,

где n – число степеней свободы движения молекул (для одноатомных газов n=3, для двухатомных n = 5, для трёх и более атомных n = 6).