Задача 5.4
Средняя продолжительность горения, установленная путем испытания 10 случайно отобранных электрических лампочек, оказалась равной 1280 ч при среднем квадратическом отклонении 18 ч.
С какой вероятностью можно утверждать, что допущенная при этом предельная ошибка выборки (т.е. расхождение между выборочной и генеральной средней) не превысит 12 ч?
Решение.
Поскольку п < 20, имеем дело с малой выборкой. Определяем среднюю ошибку малой выборки:
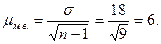
Из формулы предельной ошибки выборки находим:

Поскольку при малой выборке вероятность наступления той или иной ошибки выборки подчиняется распределению Стьюдента и, в частности, вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле
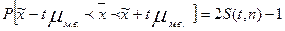 ,
,
обращаемся к соответствующей таблице, где рассчитаны вероятности S(t) (см. таблицу Приложения 3), и находим для заданных п и t (на пересечении) значение S(t), а затем уже рассчитываем 2S(t)-1. Так, в нашем примере по таблице Приложения 3 для n = 10 — 1=9 и t=2 получаем S(t) = 0,962. Отсюда искомая вероятность допуска ошибки не более 12 ч равняется 2*0,962-1= =0,924.
(Значение п в таблице Приложения 3 принимается на единицу меньше числа наблюдений, т.е. как число степеней свободы. В нашем примере число наблюдений 10, следовательно, в таблице ищем графу с п = 9.)