Задачи для самостоятельного решения

 

Вариант 1

 

С целью изучения размеров дневной выручки в сфере мелкого частного бизнеса была проведена 10%-ная случайная бесповторная выборка из 1000 торговых киосков города. В результате были получены данные о средней дневной выручке, которая составила 500 у.е. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка всех торговых точек изучаемой совокупности, если среднее квадратическое отклонение составило 150 у.е.?

 

Решение:

t=1,96

σ=150

n=100= (1000*10)/100

 

∆

Вывод:Средняя дневная выручка всех торговых точек изучаемой совокупности может находиться в пределах от 498 до 502.

 

Вариант 2

 

Фирма, торгующая автомобилями в небольшом городе, собирает информацию о состоянии местного автомобильного рынка в текущем году. С этой целью из 8 746 лиц в возрасте 18 лет и старше, проживающих в этом городе, отобрано 500 человек. Среди них оказалось 29 человек, планирующих приобрести новый автомобиль в текущем году. Оцените в генеральной совокупности долю лиц от 18 лет и старше, планирующих приобрести новый автомобиль в текущем году с вероятностью 0,95.

 

Решение:

N=8 746 n=500 m=29

t=1,96

w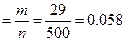

∆w

 

Вывод:

Доля от 3,8 до 7,8 лиц от 18 лет и старше, планируют приобрести новый автомобиль в текущем году.

 

Вариант 3

 

В целях изучения среднедушевого дохода семей города в 1995 году была произведена 1%-ная повторная выборка из 30 тыс. семей. По результатам обследования среднедушевой доход семьи в месяц составил 200 у.е. со средним квадратическим отклонением, равным 150 у.е. С вероятностью 0,95 найдите интервал, в котором находится величина среднедушевого дохода всех семей города, считая среднедушевой доход случайной величиной, распределенной по нормальному закону.

 

Решение:

t=1,96

n=(30000*1%)/100%= 300

x=200 у.е.

σ=150 у.е.

p=0.95

 

∆

Вывод: Величина среднедушевого дохода всех семей города находится в интервале от 183 до 217.

 

Вариант 4

 

В 1996 году выборочное обследование распределения населения города по среднедушевому денежному доходу показало, что 40% обследованных в выборке имеют среднедушевой денежный доход не более 200 у.е. В каких пределах находится доля населения, имеющего такой среднедушевой доход, во всей генеральной совокупности, если объем генеральной совокупности составляет 1 млн. единиц, выборка не превышает 10% объема генеральной совокупности и осуществляется по методу собственно-случайного бесповторного отбора, а доверительная вероятность принимается равной 0,954.

Решение:

t=2

x = 200 у.е.

n = 0,1

N = 1 млн

M = 0,04

 

 

Вариант 5

 

Строительная компания хочет оценить возможности успешного бизнеса на рынке ремонтно-строительных работ. Эта оценка базируется на случайной бесповторной выборке, в соответствии с которой из 1000 домовладельцев, собирающихся ремонтировать или перестраивать свои дома, отобраны 600 человек. По этой выборке определено, что средняя стоимость строительных работ, которую предполагает оплатить отдельный домовладелец, составляет 5000 у.е. Какова может быть предельная ошибка, если стандартное отклонение стоимости строительных работ в выборке составило 500 у.е.?

Решение:

x=5000

N = 1000 чел

n = 600

µx = 500

t = 1

Вывод: предельная ошибка отклонения стоимости строительных работ с достоверностью на 68% равна ±500 у.е.

 

Вариант 6

 

С помощью случайной выборки оценивается среднее время ежедневного просмотра телепередач абонентами кабельного телевидения в период с 18 до 22 часов. Каким должен быть объем выборки в том случае, если в предыдущих выборочных обследованиях стандартное отклонение времени просмотра передач составило 40 минут, а отклонение выборочной средней от генеральной средней по абсолютной величине не должно превышать 5 минут с вероятностью 0,99?

Решение:

n=?

x``=?

σ=40

t=3

x=5

3²*40

nx = (5)² = 14,4

Вывод: при отклонении времени просмотра передач на 40 мин. объем выборки составил 14,4.

Вариант 7

 

Для оценки остаточных знаний по общеэкономическим предметам были протестированы 25 студентов 2-го курса факультета. Получены следующие результаты в баллах:

107, 90, 114, 88, 117, 110, 103, 120, 96, 122, 93, 100, 121, 110, 135, 85, 120, 89, 100, 126, 90, 94, 99, 116, 111.

По этим данным с вероятностью 0,95 найдите интервал для оценки среднего балла тестирования всех студентов 2-го курса факультета.

Решение:

t=1.96

x = 106

n = 25

D = 25

106 ± 2

Вывод: для оценки среднего балла тестирование всех студентов необходимо использовать интервал от 104 до 108.

 

Вариант 8

 

Для изучения размера среднемесячной заработной платы занятого населения региона производится случайная повторная выборка. Каким должен быть объем этой выборки, чтобы с доверительной вероятностью 0,997 можно было утверждать, что среднемесячная заработная плата в выборке отличается от среднемесячной заработной платы работников во всем регионе оп абсолютной величине не более чем на 25%, если среднемесячная заработная плата в выборке составила 220 у.е. со средним квадратическим отклонением 120 у.е.?

 

Вариант 9

 

Выборочное исследование деятельности коммерческих банков региона показало, что в среднем каждый банк имеет 10 филиалов в регионе (со стандартным отклонением, равным 5). Найдите объем выборки, позволивший сделать такую оценку, если предельная ошибка выборочной средней находится в пределах 20% от ее фактического значения, а доверительная вероятность составляет 0,95.

 

Вариант 10

 

При выборочном опросе 1200 телезрителей оказалось, что 456 из них регулярно смотрят программы телеканала НТВ. С вероятностью 0,99 постройте интервал, оценивающий долю всех телезрителей, предпочитающих программы телеканала НТВ.

 

Вариант 11

 

По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу:

 

Среднедушевой доход семьи в месяц, у.е.	до 25	25-50	50-75	75-100	100-125	125-150	150 и выше
Количество обследованных семей

 

С вероятностью 0,95 оцените долю семей с доходом до 100 у.е. в генеральной совокупности.

 

Вариант 12

 

Известны следующие данные о заработной плате работников одного из цехов предприятия:

 

Заработная плата, у.е.	50-75	75-100	100-125	125-150	150-175	175-200	200-225
Число работников

 

С вероятностью 0,997 рассчитайте интервал, в котором может находиться средняя заработная плата на предприятии в целом.

 

Вариант 13

 

По результатам выборочного обследования торговых киосков города получены следующие данные о дневной выручке частного бизнеса:

 

Выручка от продажи товара, тыс. у.е.	до 1	1-1,2	1,2-1,4	1,4-1,6	1,6-1,8	1,8-2,0	2,0 и выше
Число торговых киосков

 

Сколько киосков необходимо обследовать, чтобы предельная ошибка выборки не превышала 500 у.е.?

 

Вариант 14

 

Имеются выборочные данные о числе сделок, заключенных брокерскими фирмами и конторами города в течение месяца:

 

Число заключенных сделок	10-30	30-50	50-70	70-90
Число брокерских фирм и контор

 

На сколько может отклоняться среднее число заключенных сделок при бесповторном обследовании, если в городе зарегистрировано 1025 брокерских фирм и контор?

 

Вариант 15

 

Известны следующие данные о дневной выручке в магазине электроники:

 

Выручка, у.е.	до 200	200-300	300-400	400-500	500-600	600-700
Число дней

 

Сколько дней в году предприятие может надеяться получать выручку выше средней? Принять 264 рабочих дня в году.