Разбор типовых задач

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

Теория вероятностей

 

Индивидуальные задания

 

Пособие разработано доцентом Цыловой Е. Г., ассистентом Морозовой Е. А.. Одобрено методической комиссией кафедры «Высшая математика» © 2007, каф. «Высшая математика» ПГТУ

 

 

Пермь 2007


Разбор типовых задач

Задача 1. В партии из 10 деталей две бракованные. Найти вероятность того, что среди выбранных на удачу четырех деталей окажется одна бракованная.

Решение:Пространство элементарных исходов представляет собой в этом случае множество всевозможных упорядоченных наборов из четырех любых деталей. Общее число таких элементарных исходов равно 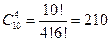. Пусть событие А состоит в том, что в выборку попадут три годных детали и одна бракованная. Три годные детали из восьми можно взять способами. Следовательно, число благоприятствующих исходов равно . Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов .

Задача 2. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка . Пусть и – координаты этой точки. Найти вероятность того, что сумма координат этой точки не превзойдет 0,5.

Решение:В прямоугольной системе координат область – квадрат со стороной 1, а область – определяется неравенством .

Область – квадрат, поэтому мера равна 1. Область – прямоугольный треугольник, катеты которого равны по 0,5. Таким образом, .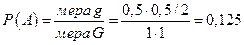

Задача 3. По каналу связи передаются три сообщения, каждое из которых может быть передано правильно или частично искажено. Вероятность того, что сообщение передано правильно – 0,8. Считая, что сообщение искажается или передается правильно не зависит от количества передач и от результата предыдущей связи найти вероятности следующих событий:

{ все три сообщения переданы верно}

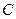{ одно из трех сообщений искажено}

{ хотя бы одно из трех сообщений искажено}

Решение:Обозначим через событие, состоящее в том, что 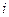-ое сообщение передано верно. Событие . Применяя теорему умножения для независимых событий и учитывая, что , вычислим .

Событие 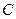можно выразить через события , и 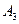следующим образом: . Применяя теорему сложения несовместных событий и теорему умножения, найдем вероятность этого события:

.

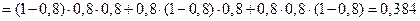Событие 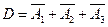. Теорему сложения для несовместных событий применить нельзя, так как события , и 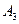совместны. Вероятность события удобно вычислять через вероятность противоположного события . Вычислим .

Задача 4. Монета подброшена 5 раз. Какова вероятность, что герб появится не более 2 раз?

Решение:В этой задаче . По формуле Бернулли находим вероятность события .

.

Задача 5. Производится 400 выстрелов по мишени. Вероятность попадания при одном выстреле равна 0,8. Найти: а) наивероятнейшее число попаданий; б) вероятность 320 попаданий в мишень; в) вероятность того, что число попаданий в мишень будет не менее 300 и не более 350.

Решение:а) найдем наивероятнейшее число попаданий в мишень из неравенства 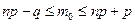. По условию задачи . Тогда получим , значит, .

б) при больших ( 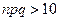) имеет место приближенное равенство (локальная теорема Лапласа):

.

в) при больших ( 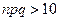) имеет место приближенное равенство (интегральная теорема Лапласа): . На основании этой формулы получим:

.

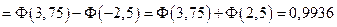Задача 6. Вероятность того, что деталь нестандартна, равна =0,1. Сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544,можно было бы утверждать, что относительная частота появления нестандартной детали отклонится от вероятности не более, чем на 0,03?

Решение:По условию ; . Для решения воспользуемся формулой: . В силу условия задачи 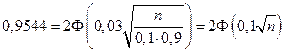. По таблице находим . Отсюда или .

Задача 7.Определить надежность схемы, если Pi – надежность i – го элемента

Решение.Для работы схемы необходимо, чтобы одновременно происходили следующие события:

А={работал хотя бы один из элементов };

В={работал хотя бы один из элементов };

С={работал элемент };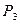

D={работал элемент };

Е={ работал хотя бы один из элементов };

Вычислим вероятности этих событий:

Р(А)= ;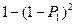

Р(В)= ;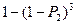

Р(С)= ;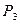

Р(D)= ;

Р(Е)= .

События А, В, С, D, Е – независимы, по теореме умножения вероятностей получим:

Р=[ ][ ] [ ].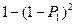

 

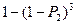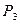
Решение остальных заданий варианта базируется на одних и тех же свойствах и теоремах, а поэтому решаются аналогично.[1]


Вариант №1

  1. Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»?
  2. Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков четное.
  3. В квадрат с вершинами в точках (0,0), (0,1), (1,1), (1,0) наудачу брошена точка (х,у). Найдите вероятность того, что координаты этой точки удовлетворяют неравенству у<2х.
  4. Имеется пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что

а) все три билета стоят вместе семь рублей,

б) все три билета стоимостью по одному рублю.

  1. Из урны, содержащей 5 белых шаров и 5 черных, наудачу достают 6 штук. Найти вероятность того, что среди вынутых шаров окажется одинаковое число черных и белых (шары отличаются только цветом).
  2. Двадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся выучил 35 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого нужно ответить на два вопроса билета или на один вопрос билета и один дополнительный вопрос из другого билета.
  3. Из урны, содержащей 5 шаров с номерами от 1 до 5, последовательно извлекаются два шара, причем первый шар возвращается, если номер не равен единице. Определить вероятность того, что шар с номером два будет извлечен при втором извлечении.
  4. В каждой из двух урн находятся 5 белых шаров и 10 черных. Из первой урны во вторую наудачу переложили один шар, а затем из второй урны наугад вынули один шар. Найти вероятность того, что шар, вынутый из второй урны, окажется белым.
  5. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
  6. В семье пять детей. Найти вероятность того, что среди этих детей:

а) два мальчика,

б) не более двух мальчиков,

в) более двух мальчиков,

г) не менее двух и не более трех мальчиков.

Принять вероятность рождения мальчика равной 0,51.

  1. Вероятность получения бракованной детали равна 0,01. Какова вероятность того, что среди 400 деталей бракованных окажется:

а) 3 детали;

б) хотя бы одна.

  1. При передаче сообщения на расстояние вероятность искажения одного знака равна 0,01. Какова вероятность того, что при передаче сообщения из 300 знаков: а) не будет ни одного искажения, б) будет два искажения, в) будет хотя бы одно искажение?
  2. Определить надежность схемы, если Pi – надежность i – го элемента

 

Вариант №2

  1. Числа 1,2,3,4,5 написаны на пяти карточках. Наугад последовательно выбираются три карточки и располагаются в порядке появления слева направо. Найти вероятность того, что полученное при этом трехзначное число будет четным.
  2. Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков равно 8.
  3. На отрезок АВ длиной 12 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет между 36 см2 и 81 см2.
  4. В лотерее N билетов, из которых M выигрышных. Участник купил k билетов. Какова вероятность того, что он ни по одному билету не выиграет?
  5. В ящике 10 деталей, среди которых 5 бракованных. Наудачу достают 3 детали. Найти вероятность следующих событий:

а) все детали окажутся годными;

б) две детали окажутся годными и одна бракованная.

  1. Какова вероятность, что наудачу выбранное пятизначное число содержит только нечетные цифры?
  2. Из ящика, где 12 деталей 1 категории и 20 деталей второй категории, наудачу без возвращения извлекли 2 детали. Найти вероятность того, что вторая деталь 1 категории.
  3. В каждой из двух урн имеются по 7 белых и 3 черных шара. Из первой урны во вторую наудачу переложены два шара. После этого из второй урны наудачу достают один шар. Какова вероятность что он окажется белый?
  4. Две перфораторщицы набили на перфораторах по одному комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. Предполагается ,что оба перфоратора были исправны.
  5. Монету подбрасывают 100 раз. Найти наивероятнейшее число появлений герба и вероятность такого результата.
  6. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
  7. Пусть вероятность нарушения герметичности банки консервов равна 0,0005.Найти вероятность того, что среди 2000 банок две окажутся с нарушением герметичности.
  8. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №3

  1. Два игрока бросают монету по два раза каждый. Выигравшим считается тот, кто получит больше гербов. Найти вероятность того, что выигрывает первый игрок.
  2. Устройство секретного замка включает в себя 4 ячейки. В первой ячейке осуществляется набор одной из четырех букв A, B, C, D, в трех остальных – одной из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (цифры могут повторяться). Чемуравнавероятность того, что замок будет открыт с первой попытки?
  3. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 10 см. На плоскость наудачу бросается монета радиуса 2 см. Найти вероятность того, что монета не пересечет ни одной из прямых.
  4. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
  5. В ящике лежат 10 красных, 8 синих и 5 зеленых шаров; шары отличаются только цветом. Наудачу вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся одного цвета?
  6. Два игрока поочередно бросают монету. Выигрывает тот, кто первым получит герб. Найти вероятность выигрыша для первого игрока.
  7. В лотерее 100 билетов из которых 20 выигрышных. Участник покупает два билета. Определить вероятность того, что хотя бы один билет будет выигрышным.
  8. По самолету производится два выстрела, вероятность попадания при каждом равна 0,6. При одном попадании самолет будет сбит с вероятностью 0,5, при двух – с вероятностью 0,9. Какова вероятность, что самолет будет сбит?
  9. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
  10. Вероятность появления события А в каждом опыте равна 0,3. Опыт повторяется 5 раз. Найти вероятность того, что событие появляется не более 2 раз.
  11. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не белее чем на 0,02.
  12. Вероятность появления события в одном испытании равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,95 можно было ожидать отклонение относительной частоты появления события от его вероятности не более, чем на 0,05.
  13. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №4

  1. В лифт девятиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий:

А) – все пассажиры выйдут на одном этаже.

В) – все пассажиры выйдут на разных этажах.

  1. Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, не превзойдет 6.
  2. Каждое их двух чисел неотрицательно, но меньше 2. Найти такие два числа, сумма которых не больше 2,5, а произведение больше 4.
  3. В урне «а» белых шаров и «в» черных (а>2). Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми?
  4. В урне 8 шаров: 3 белых и 5 черных. Какова вероятность того, что вынутые наугад два шара окажутся:

а) белые;

б) черные;

в) одного цвета.

  1. Радист трижды вызывает корреспондента. Причем следующий вызов производится при условии, что предыдущий вызов не принят. Вероятность принятия первого вызова равна 0,3, второго – 0,4, третьего – 0,5. Найти вероятность того, что вызов будет принят.
  2. На карточках написаны цифры 2,3,4,5,6,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры нечетные.
  3. В ящике содержится 12 деталей завода №1, 20 деталей завода №2; 18 деталей завода №3. Вероятность того, что деталь завода №1 отличного качества, равна, 0,9; для деталей заводов №2 и №3 вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
  4. Известно, что 5% мужчин и 0,25 всех женщин дальтоники. Наудачу выбранное лицо – дальтоник. Какова вероятность того, что это мужчина? (считать, что мужчин и женщин одинаковое количество).
  5. Найти вероятность того, что при пяти подбрасываниях игрального кубика единица появляется хотя бы один раз.
  6. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти число испытаний , при котором с вероятностью 0,9876 можно ожидать, что относительная частота появления события отклоняется от его вероятности по абсолютной величине не более чем на 0,04.
  7. Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний , при котором с вероятностью 0,9973 можно ожидать, что относительная частота появления события отклониться от его вероятности по абсолютной величине не более, чем на 0,02.
  8. Определить надежность схемы, если Pi – надежность i – го элемента

 

Вариант №5

  1. На пяти карточках написаны цифры 1,2,3,4,5. Две из них, одна за другой, вынимаются. Найти вероятность того, что число на второй карточке будет больше, чем на первой.
  2. Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, равна 8.
  3. На окружности выбрана некоторая точка А, через которую проводится случайная хорда. Какова вероятность, что длина хорд будет больше стороны правильного вписанного шестиугольника?
  4. В урне 7 белых шаров и 3 черных. Наудачу достают 2 шара. Какова вероятность того, что они разного цвета.
  5. Среди 6 лотерейных билетов 2 выигрышных. Наудачу берут два билета. Какова вероятность того, что среди них окажется:

а) один выигрышный;

б) два выигрышных.

  1. На карточках написаны цифры 4,5,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры окажутся нечетными?
  2. В первой урне имеется 3 белых и 2 черных шара, во второй 4 белых и 6 черных. Шары отличаются только цветом. Из каждой урны достают по одному шару. Какова вероятность, что они окажутся одного цвета?
  3. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
  4. В урне находится один шар, о котором известно, что он либо белый, либо черный. В урну положили белый шар, а потом после тщательного перемешивания вынули наудачу один шар, который оказался белым. Какова вероятность того, что после этого вынут из урны белый шар?
  5. Вероятность попадания в мишень хотя бы один раз при двух выстрелах для данного стрелка равна 0,99. Найти вероятность попадания в мишень данным стрелком при одном выстреле.
  6. Вероятность появления события в каждом из 10000 независимых испытаний равна 0,75. Найти такое положительное 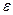, что с вероятностью 0,979 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,75 не превысит .
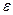  7. Завод отправил на базу 1000 изделий. Вероятность повреждения изделий в пути 0,002. Найти вероятность того, что в пути будет повреждено не более трех изделий.
  8. Определить надежность схемы, если Pi – надежность i – го элемента

 

Вариант №6

  1. Какова вероятность того, что в выбранном наудачу двухзначном числе цифры: а) одинаковые; б) различные.
  2. На карточках написаны цифры 1,2,3,4,5. Наудачу достают две карточки. Какова вероятность, что сумма цифр на них будет четной?
  3. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение больше 2/9?
  4. В урне 5 белых шаров, 3 черных и 6 красных. Наудачу достают 5 шаров. Какова вероятность того, что в выборку попадут 2 белых, 2 черных и 1 красный шар.
  5. Партия из 15 деталей содержит 3 бракованные. Контролер для проверки наудачу берет 5 деталей. Если среди отобранных деталей не будет обнаружено бракованных деталей, то партия принимается. Найти вероятность того, что данная партия будет принята.
  6. В связке имеется 6 ключей, из которых только один подходит к двери. Найти вероятность того, что на открывание потребуется не более четырех опробований. Предполагается, что опробованный ключ в дальнейших опробованиях не участвует.
  7. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95, для полотера такая вероятность равна 0,9. Найти вероятность того, что

а) оба прибора выдержат гарантийный срок;

б) хотя бы один выдержит гарантийный срок.

  1. Вероятности того, что во время работы цифровой электронной машины возникает сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
  2. Урна содержит шаров. Все предположения о числе белых шаров в урне равновозможны. Наудачу выбранный из урны шар оказался белым. Вычислить вероятность всех предположений о составе шаров в урне. Какое предположение наиболее вероятно.
  3. Вероятность изготовления прибора повышенного качества равна 0,74. Найти наивероятнейшее число приборов повышенного качества в партии из 80 приборов и вероятность этого результата.
  4. Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,9426 границы, в которых будет заключено число бракованных изделий среди проверенных.
  5. Вероятность появления события в каждом из независимых испытаний равна 0,7. Найти вероятность того, что при 400 испытаниях событие появится 300 раз.
  6. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №7

  1. Брошены две игральные кости. Какова вероятность, что сумма выпавших очков не менее 9?
  2. Вероятность того, что в течение одной смены возникает неполадка станка, равна 0,1. Найти вероятность того, что не пройдет ни одной неполадки за три смены.
  3. На отрезке АВ длины l поставлена наудачу точка М. Какова вероятность того, что расстояние этой точки от середины отрезка меньше, чем расстояние этой точки до ближайшего края.
  4. В урне N белых шаров и M черных. Надуачу извлекается K шаров (K>M).Какова вероятность того, что в урне остались только белые шары?
  5. В ящике имеется 5 красных шаров и 3 синих, шары отличаются только цветом. Наудачу достают два шара. Найти вероятности того, что оба шара окажутся:

а) одного цвета;

б) разного.

  1. Бросаются одновременно две игральные кости. Найти вероятность того, что произведение выпавших очков будет четным.
  2. Рабочий обслуживает три станка. Вероятность того, что в течение часа для первого станка потребуется внимание рабочего, равна 0,3, для второго – эта вероятность равна 0,2, для третьего – 0,15. Какова вероятность того, что

1) для всех трех станков потребуется внимание рабочего,

2) ни для одного не потребуется внимания.

  1. Электролампы изготовляются на 3-х заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что приобретенная в магазине лампа стандартная?
  2. В пирамиде установлено 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
  3. Найти наиболее вероятное число попаданий в мишень при 210 выстрелах и вероятность такого результата, если вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7.
  4. Сто станков работают независимо друг от друга. Вероятность бесперебойной работы каждого из них в течение смены равна 0,8. Найти вероятность того, что в течение данной смены безотказно поработают 85 станков.
  5. Вероятность изготовления бракованного генератора автомобильного двигателя равна 0,0003. Определить вероятность того, что в изготовленной партии из 200 шт. окажется хотя бы один бракованный.
  6. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №8

  1. Из букв слова «ротор», составленного из букв разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор».
  2. Бросаются четыре игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
  3. На плоскости нанесена сетка квадратов со стороною «а». На плоскость наудачу брошена монета радиуса . Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от ее расположения.
  4. Студент знает 30 из 40 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.
  5. На складе имеются 8 изделий, 3 из них изготовлены заводом N. Найтивероятность того, что среди 4 наудачу взятых изделий окажется не более половины, изготовленных заводом N.
  6. Вероятность успешной попытки выполнить упражнение для каждого из двух спортсменов равна 0,5. Спортсмены упражнение выполняют по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
  7. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на любой вопрос билета, равна 0,9. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса билета.
  8. На фабриках «а», «в» и «с» производят соответственно 25, 35 и 40% всех изделий. В их продукции брак составляет соответственно 5,4 и 2 %. Какова вероятность того, что случайно выбранное изделие, произведенное на фабрике, дефектно?
  9. В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% с заболеванием L, 20% с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезни L и M эти вероятности соответственно равны0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.
  10. Вероятность того, что малое предприятие за год станет банкротом равна 0,2. Найти вероятность того, что из 10 малых предприятий за год сохранятся хотя бы два.
  11. Вероятность появления события в каждом из независимых опытов равна 0,95. Найти вероятность того, что событие появится не менее 1800 раз в 2000 опытах.
  12. Всхожесть семян ржи составляет 90%. Найти вероятность того, что из 10000 посеянных семян взойдет 900.
  13. Определить надежность схемы, если Pi – надежность i – го элемента

 

Вариант №9

  1. Буквенный замок содержит в общей оси 4 диска, каждый из которых разделен на 6 секторов с различными нанесенными на них буквами. Замок открывается в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Определить вероятность того, что замок откроется, если установлена произвольная комбинация букв.
  2. Какова вероятность, что наудачу взятое трехзначное число будет четным?
  3. На отрезке ОА длиною L числовой оси ОХ наудачу поставлены две точки В(х) и С(у), причем . (Координата точки С обозначена через у для удобства дальнейшего изложения). Найти вероятность того, что длина отрезка ВС будет меньше длины отрезка ОВ. Предполагается ,что вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения на числовой оси.
  4. В корзине 12 белых теннисных мячей, 10 красных и 6 синих. Наудачу достают два мяча. Какова вероятность, что они окажутся одного цвета?
  5. В ящике лежат 11 одинаковых по форме пуговицы, из них: 5 черных пуговиц. Работнице требуется пришить к очередному пальто 4 черные пуговицы. Определить вероятность того, что среди наугад взятых 4 пуговиц все пуговицы черные.
  6. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,7, для второго станка эта вероятность равна 0,8, для третьего – 0,9, для четвертого – 0,85. Найти вероятность того, что в течение часа по крайней мере один станок потребует к себе внимания рабочего.
  7. На карточках написаны цифры 1,2, … , 20. Наудачу берут две карточки. Найти вероятность того, что одна выбранная цифра меньше 10, а вторая больше 10.
  8. В двух урнах содержатся соответственно и шаров, из них белых шаров и . Из первой урны переложили в другую один шар, цвет которого неизвестен. После этого из другой урны берут один шар. Какова вероятность того, что он белый?
  9. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны ; ; .
  10. Найти вероятность того, что при 5 бросаниях монеты число появлений герба будет больше числа появлений решек.
  11. Для данного стрелка вероятность попадания в мишень при одном выстреле равна 0,9. Произведено 1000 выстрелов по мишени. Найти вероятность того, что число попаданий будет менее 80 и не более 95.
  12. Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний , при котором с вероятностью 0,9973 можно ожидать, что относительная частота появления события отклониться от его вероятности по абсолютной величине не более, чем на 0,02.
  13. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №10

  1. На карточках написаны цифры 1,2,3,4,5. Наудачу достают две карточки. Какова вероятность, что сумма цифр на них будет четной?
  2. Из последовательности чисел 1,2,…,100 наудачу выбираются 2 числа. Какова вероятность, что одно из них меньше 30, а другое больше 30?
  3. В квадрате с вершинами (0,0), (0,2), (2,2) и (2,0) наудачу берется точка (х,у). Какова вероятность того, что ?
  4. Партия из 15 деталей содержит 3 бракованные. Контролер для проверки наудачу берет 5 деталей. Если среди отобранных деталей не будет обнаружено бракованных деталей, то партия принимается. Найти вероятность того, что данная партия будет принята.
  5. В ящике в случайном порядке разложено двадцать деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что, по крайней мере, одна из этих деталей окажется стандартной.
  6. Рабочий обслуживает три станка, вероятность того, что в течение часа для первого станка не потребуется помощь рабочего равна 0,9, для второго – 0,8, для третьего – 0,7. Найти вероятность того, что, по крайней мере, для двух станков не потребуется помощь рабочего.
  7. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9; для второго и третьего орудий эти вероятности соответственно равны 0,5 и 0,8. Найти вероятность того, что

а) только один снаряд попадет в цель;

б) все три снаряда попадут в цель.

  1. Радиолокационная станция ведет наблюдение за объектом, который может создавать помехи. Если объект не создает помехи, то за один цикл осмотра станция обнаруживает его с вероятностью , если создает – с вероятностью ( < ). Вероятность того, что во время цикла осмотра будут созданы помехи, равна в других циклах. Найти вероятность обнаружения объекта, по крайней мере, один раз за 1 цикл осмотра.
  2. В ящик, где 10 деталей 1-го сорта и 3 детали 2-го сорта, токарь положил одну изготовленную деталь. После чего сборщик взял наудачу из ящика одну деталь, которая оказалась первого сорта. Найти вероятность того, что вложенная токарем деталь была 2-ого сорта, если он изготавливает детали только 1-го и 2-го сортов с вероятностями 0,95 и 0,5 соответственно.
  3. Вероятность рождения мальчика равна 0,515. Найти вероятность того, что из 20 новорожденных будет 11 мальчиков.
  4. Вероятность появления события в каждом из независимых испытаний равна 0,9. Сколько нужно произвести испытаний, чтобы с вероятностью не меньшей 0,8 можно было ожидать, что отклонение относительной частоты от вероятности появления события в одном испытании равной 0,9 не превзойдет 0,2.
  5. Вероятность неточной сборки прибора равна 0,1. Найти вероятность того, что среди 900 приборов окажется от 750 до 850 точных.
  6. Определить надежность схемы, если Pi – надежность i – го элемента

Вариант №11

  1. На карточках написаны цифры 1,2,3,4,5,6,7. Наудачу взяли две карточки. Какова вероятность, что одно число будет меньше трех, а другое больше трех?
  2. Лотерея выпущена на общую сумму N р. Цена одного билета р. Ценные выигрыши попадают на билетов. Определите вероятность ценного выигрыша на один билет.
  3. Найти вероятность события , если х и у – координаты точки М(х, у), брошенной в квадрат , .
  4. В ящике 12 красных и 4 синих пуговиц. Вынимают наугад две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
  5. В группе 25 студентов из них 5 отличников. Какова вероятность того, что среди 7 наугад выбранных по списку студентов 3 отличника.
  6. Вероятность попадания в мишень для данного стрелка равна 0,7. Стрелок делает два выстрела по мишени. Найти вероятности следующих событий:

а) стрелок попадет 2 раза;

б) попадет один раз;

в) попадет хотя бы один раз.

  1. В лотерее 100 билетов, из которых 10 выигрышных. Участник покупает три билета. Определить вероятность того, что хотя бы один билет будет выигрышным.
  2. В урну, которая содержит шаров, положили белый шар. Какова вероятность того, что вынутый из урны шар будет белым, если все предположения о начальном составе урны равновероятны.
  3. Из урны, содержащей 7 белых и 12 черных шаров, наудачу без возвращения извлекли 2 шара. Что вероятнее: первый извлеченный шар был белым или черным, если известно, что второй извлеченный шар оказался белым.
  4. Электронная система состоит из 28 блоков, каждый из которых может отказать в течение года с вероятностью 0,05. Найти наиболее вероятное число отказов и его вероятность.
  5. Игральный шестигранный кубик подбрасывается 500 раз. Какова вероятность того, что отклонение относительной частоты появления шестерки от вероятности ее появления в одном опыте по абсолютной величине не превзойдет 0,1?
  6. Всхожесть семян некоторого растения равна 0,9. Какова вероятность того, что из 100 посеянных семян взойдет не менее 80.
  7. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №12

  1. По ячейкам случайно распределяются предметов. Найти вероятность, что все предметы попадут в одну ячейку.
  2. Три предмета распределяются по 5 ячейкам случайным образом. Найти вероятность того, что все они попадут в разные ячейки
  3. Плоскость разграфлена прямоугольниками со сторонами 6 и 4 см. На плоскость брошен круг радиуса 1 см. Какова вероятность, что он не пересечет ни одну из линий.
  4. Ящике лежат одинаковые по форме пуговицы: 6 черных и 5 белых. Работнице требуется пришить к очередному пальто 3 черные пуговицы. Определить вероятность того, что среди наугад взятых 5 пуговиц имеется нужное количество черных пуговиц.
  5. Студент из 15 вопросов знает ответы только на 7 вопросов. Определить вероятность того, что из 5 наугад выбранных вопросов он знает ответы на 3 вопроса.
  6. Вероятность появления события в одном испытании равна 0,7. Найти вероятность того, что среди пяти испытаний удачных будет не более двух.
  7. В урне 7 белых шаров, 3 черных и 2 красных. Наудачу достают два шара. Найти вероятность того, что они оба окажутся одного цвета.
  8. В пирамиде установлены 5 винтовок, из которых 3 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
  9. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру, равна, 0,55, а ко второму – 0,45. Вероятность пропустить нестандартные изделия для первого контролера равна 0,01, для второго – 0,02. Взятое наудачу изделие с маркой «стандарт» оказалось бракованным. Какова вероятность, что изделие проверялось вторым контролером?
  10. В ходе аудиторской проверки компании аудитор случайным образом отбирает 5 счетов. Найти вероятность того, что обнаружит 1 счет с ошибкой, если ошибки содержат в среднем 3% счетов.
  11. Вероятность наступления события в одном опыте равна 0,6. Вычислить вероятность того, при 6000 испытаниях событие произойдет не менее 340 и не более 380 раз.
  12. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится:

а) не менее 1470 и не более 1500 раз;

б) не менее 1470 раз;

в) не более 1469 раз.

  1. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №13

  1. Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков равно 8.
  2. Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»?
  3. Определить вероятность того, что корни квадратного уравнения вещественны, если и .
  4. Определить вероятность того, что партия из ста изделий, среди которых пять бракованных, будет принята при испытании наудачу выбранной половины всей партии, если условиями приема допускается наличие бракованных изделий не более одного из пятидесяти.
  5. Имеется пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что
  6. В одной урне 5 белых шаров и 4 черных, во второй – 4 белых и 6 черных. Наудачу достают по одному шару из каждой урны. Какова вероятность того, что среди вынутых шаров окажется:

а) один белый шар;

б) два белых шара.

  1. В кармане имеются 10 монет по 20 к., 5 монет по 15 к. и 2 монеты по 10 к. Наудачу берется 6 монет. Какова вероятность того, что в сумме они составят не более одного рубля.
  2. Имеются три станка. На первом станке токарь изготавливает деталь высшего сорта с вероятностью 0,95 ,на втором и третьем с вероятностями 0,9 и 0,8 соответственно. На случайно выбранном станке теперь изготовили одну деталь. Какова вероятность того, что эта деталь будет высшего сорта.
  3. В ремесленном цехе трудятся 3 мастера и 6 их учеников. Мастер допускает брак при изготовлении изделия с вероятностью 0,05; ученик – с вероятностью 0,15. Поступившее из цеха изделие оказалось бракованным. Какова вероятность, что его изготовил мастер?
  4. В среднем 20% акций на аукционе продается по первоначально заявленной стоимости .Найти вероятность того, что из 10 пакетов акций в результате торгов будут проданы не менее двух пакетов акций.
  5. Произведено 1000 независимых испытаний, вероятность появления события в одном испытании равна 0,7. Оценить вероятность того, что отклонение относительной частоты появления события от вероятности 0,7 по абсолютной величине не превзойдет 0,1.
  6. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
  7. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №14

  1. Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков четное.
  2. Числа 1,2,3,4,5 написаны на пяти карточках. Наугад последовательно выбираются три карточки и располагаются в порядке появления слева направо. Найти вероятность того, что полученное при этом трехзначное число будет четным.
  3. В круге радиуса R наудачу выбрана точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
  4. Абонент забыл последнюю цифру номера телефона и поэтому набирает ее наудачу. Определитьвероятность того, что ему придется звонить не более чем в четыре места.
  5. В лотерее N билетов, из которых M выигрышных. Участник купил k билетов. Какова вероятность того, что он ни по одному билету не выиграет?
  6. Из группы, где 8 мужчин и 5 женщин, наудачу выбрали 3 человека. Найти вероятность того, что среди выбранных лиц будет, по крайней мере, одна женщина.
  7. Из урны, содержащей 5 шаров с номерами от 1 до 5, последовательно извлекаются два шара, причем первый шар возвращается, если номер не равен единице. Определить вероятность того, что шар с номером два будет извлечен при втором извлечении.
  8. В первой группе из 25 студентов – 10 юношей, во второй из 20 студентов – 8 юношей. Из наудачу выбранной группы случайно выбрали одного студента для дежурства. Найти вероятность того, что дежурный-юноша.
  9. В данный район изделия поставляются двумя фирмами в соотношении 5:8. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%. Взятое наугад изделие оказалось стандартным. Найти вероятность того, что оно изготовлено первой фирмы.
  10. В 10% случаев страховая компания выплачивает по договорам страховку. Найти вероятность того, что по истечение срока 10 договоров компания уплатит страховку в 2 случаях.
  11. Вероятность появления события в одном опыте равна 0,9. Произведено 900 опытов. Найти наивероятнейшее число появлений события и вероятность такого результата.
  12. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не белее чем на 0,02.
  13. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №15

  1. Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, не превзойдет 6.
  2. Два игрока бросают монету по два раза каждый. Выигравшим считается тот, кто получит больше гербов. Найти вероятность того, что выигрывает первый игрок.
  3. Из отрезка [0, 2] наудачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам .
  4. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
  5. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
  6. В кармане имеются 10 монет по 20 к., 5 монет по 15 к. и 2 монеты по 10 к. Наудачу берется 6 монет. Какова вероятность того, что в сумме они составят не более одного рубля.
  7. Из ящика, где 12 деталей 1 категории и 20 деталей второй категории, наудачу без возвращения извлекли 2 детали. Найти вероятность того, что вторая деталь 1 категории.
  8. Из ящика, где 12 деталей 1 категории и 20 деталей второй категории, наудачу без возвращения извлекли 2 детали. Найти вероятность того, что вторая деталь 1 категории. На сборку поступают детали с трех автоматов. Известно, что первый автомат дает 0,3 брака, второй – 0,2, третий – 0,4. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000 деталей, со второго – 2000, с третьего – 2500.
  9. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру, равна, 0,35, а ко второму – 0,65. Вероятность пропустить нестандартные изделия для первого контролера равна 0,03, для второго – 0,01. Взятое наудачу изделие с маркой «стандарт» оказалось бракованным. Какова вероятность, что изделие проверялось первым контролером?
  10. Вероятность того, что пассажир опоздает к поезду, равна 0,01. Найти наиболее вероятное число опоздавших из 500 пассажиров.
  11. Оценить вероятность того, что появление герба в 500 испытаниях будет не менее 200 и не более 300 раз.
  12. Вероятность появления события в каждом из 400 испытаний равна 0,2. Найти вероятность того, что отклонение относительной частоты появления события от его вероятности по абсолютной величине не превзойдет 0,05.
  13. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №16

  1. Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, равна 8.
  2. Брошены две игральные кости. Какова вероятность, что сумма выпавших очков не менее 9?
  3. Точка брошена в круг радиуса R. Найдите вероятность того, что она попадает внутрь данного вписанного квадрата.
  4. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что два наудачу выбранных билета окажутся выигрышными.
  5. В урне N белых шаров и M черных. Надуачу извлекается K шаров (K>M).Какова вероятность того, что в урне остались только белые шары?
  6. В урне 7 белых шаров, 3 черных и 2 красных. Наудачу достают два шара. Найти вероятность того, что они оба окажутся одного цвета.
  7. В лотерее 100 билетов из которых 20 выигрышных. Участник покупает два билета. Определить вероятность того, что хотя бы один билет будет выигрышным.
  8. Рабочий работает на 3-х станках, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.
  9. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
  10. В семье пять детей. Найти вероятность того, что среди этих детей:

а) два мальчика,

б) не более двух мальчиков,

в) более двух мальчиков,

г) не менее двух и не более трех мальчиков.

Принять вероятность рождения мальчика равной 0,51.

  1. Произведено 800 испытаний, вероятность появления события в одном опыте равна 0,8. Вычислить вероятность неравенства .
  2. Вероятность появления события в каждом из 400 испытаний равна 0,2. Найти вероятность того, что отклонение относительной частоты появления события от его вероятности по абсолютной величине не превзойдет 0,05.
  3. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №17

  1. Вероятность того, что в течение одной смены возникает неполадка станка, равна 0,1. Найти вероятность того, что не пройдет ни одной неполадки за три смены.
  2. В лифт девятиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий:

А – все пассажиры выйдут на одном этаже.

В – все пассажиры выйдут на разных этажах.

  1. Расстояние от пункта А до В автобус проходит за 2 мин, а пешеход — за 15 мин. Интервал движения автобусов 25 мин. Вы подходите в случайный момент времени к пункту А и отправляетесь в В пешком. Найдите вероятность того, что в пути вас догонит очередной автобус.
  2. У распространителя имеется 20 билетов книжной лотереи, среди которых 7 выигрышных. Куплено 3 билета. Найтивероятность того, что хотя бы один из купленных билетов выигрышный.
  3. В урне «а» белых шаров и «в» черных (а>2). Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми?
  4. В лотерее 100 билетов, из которых 10 выигрышных. Участник покупает три билета. Определить вероятность того, что хотя бы один билет будет выигрышным.
  5. На карточках написаны цифры 2,3,4,5,6,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры нечетные.
  6. По самолету было произведено три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолет сбивается с вероятностью 0,8, при двух с вероятностью – 0,6, при трех – сбивается наверняка. Найти вероятность того, что самолет сбит.
  7. Две перфораторщицы набили на перфораторах по одному комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. Предполагается ,что оба перфоратора были исправны.
  8. Монету подбрасывают 100 раз. Найти наивероятнейшее число появлений герба и вероятность такого результата.
  9. Вероятность появления события в каждом из независимых испытаний равна 0,4. Найти наименьшее число испытаний при котором с вероятностью 0,9 можно ожидать, что относительная частота появления события отклонится от вероятности его по абсолютной величине не более, чем на 0,01 (применить интегральную теорему Лапласа).
  10. Произведено 800 испытаний, вероятность появления события в одном опыте равна 0,8. Вычислить вероятность неравенства .
  11. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №18

  1. Какова вероятность, что наудачу взятое трехзначное число будет четным?
  2. Из букв слова «ротор», составленного из букв разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор».
  3. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса г < а. Найдите вероятность того, что монета не пересечет ни од ной из прямых.
  4. В ящике лежат 11 одинаковых по форме пуговицы, из них: 5 черных пуговиц. Работнице требуется пришить к очередному пальто 4 черные пуговицы. Определить вероятность того, что среди наугад взятых 4 пуговиц все пуговицы черные.
  5. Студент знает 30 из 40 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.
  6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9; для второго и третьего орудий эти вероятности соответственно равны 0,5 и 0,8. Найти вероятность того, что

а) только один снаряд попадет в цель;

б) все три снаряда попадут в цель.

  1. В первой урне имеется 3 белых и 2 черных шара, во второй 4 белых и 6 черных. Шары отличаются только цветом. Из каждой урны достают по одному шару. Какова вероятность, что они окажутся одного цвета?
  2. Заготовки поступают из двух бункеров: 70% из первого и 30-% из второго. При этом материал первого бункера имеет 10% брака, а второго – 20%. Какова вероятность того, что наудачу взятая заготовка бракованная.
  3. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
  4. Вероятность появления события А в каждом опыте равна 0,3. Опыт повторяется 5 раз. Найти вероятность того, что событие появляется не более 2 раз.
  5. Монету подбрасывают 900 раз. Найти вероятность того, что герб выпадет: а) 400 раз, б) не менее 400 раз, в) не менее 400 и не более 500 раз.
  6. Вероятность появления события в каждом из независимых испытаний равна 0,4. Найти наименьшее число испытаний при котором с вероятностью 0,9 можно ожидать, что относительная частота появления события отклонится от вероятности его по абсолютной величине не более, чем на 0,01 (применить интегральную теорему Лапласа).
  7. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента

Вариант №19